问题
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!
Example:
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6总体思路:看每个柱子,是否能蓄水?
通过观察,我们发现每一个柱子上面能储存的最大的水量其实就是它左边的最大柱子和右边最大柱子高度差的绝对值再减去当前柱子的高度。最后再把这个差值累和即可。
解法一(动态规划,针对每个柱子计算可蓄水的量):
- 第一遍在 dp[i] 中存入i位置左边的最大值;
- 第二遍遍历数组,第二次遍历时找右边最大值,然后和左边最大值比较取其中的较小值,然后跟当前值 A[i] 相比,如果大于当前值,则将差值存入结果
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
int trap(vector<int>& height) {
int res = 0, mx = 0, n = height.size();
vector<int> dp(n, 0);
for (int i = 0; i < n; ++i) {
dp[i] = mx;
mx = max(mx, height[i]);
}
mx = 0;
for (int i = n - 1; i >= 0; --i) {
if (min(dp[i], mx) > height[i] ) res += min(dp[i], mx) - height[i];
mx = max(mx, height[i]);
}
return res;
}
int main()
{
int a[] = { 2, 6, 7, 1, 5, 6, 7, 2 ,5, 3};
vector<int> height(a, a + sizeof(a)/sizeof(int));
int res = trap(height);
cout<<"res: " << res <<endl;
return 1;
}思路二:基于Stack的回溯
- 初始化一个栈用于存放柱子的号码(下标),当栈为空或者当前柱子的高度小于等于栈顶高度时,则把当前高度的坐标压入栈
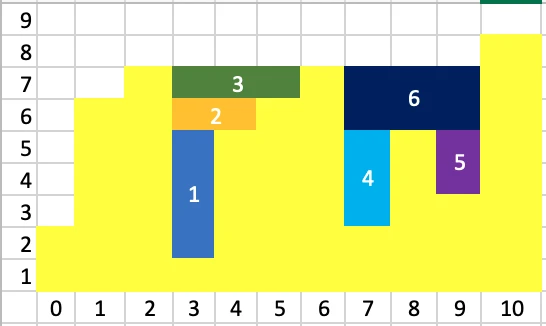
- 遍历到下一个柱子,如果高度比栈顶高度大的时候,如果栈内只有一个元素的话,直接跳过继续遍历;如果多余一个元素的话,那么此时把栈顶元素取出来当作坑,新的栈顶元素就是左边界,当前高度是右边界,取二者较小的,再减去坑的高度,长度就是右边界坐标减去左边界坐标再减1,二者相乘就是盛水量,如下图 1~ 6的区域就是从左到右计算的需水量。
int trap(vector<int>& height) {
stack<int> st;
int i = 0, res = 0, n = height.size();
while (i < n) {
if (st.empty() || height[i] <= height[st.top()]) {
st.push(i++);
} else {
int t = st.top();
st.pop();
if (st.empty()) continue;
res += (min(height[i], height[st.top()]) - height[t]) * (i - st.top() - 1);
}
}
return res;
}
