一、背景介绍
1.1 问题背景
由于机器学习和深层人工神经网络的兴起,出现了超过十亿个变量的优化问题。数据的普遍性也导致了在很多数据分析和学习问题上出现了大规模优化问题,如:飞机机翼和涡轮叶片的目标形状设计,卫星布局设计,大规模生物系统的评估,地震波形反演,供水系统的参数设定等。
高维优化问题的一个主要难点在于,当决策变量增加时,搜索空间是呈指数增长的,称为“维度灾难”。当前处理高维问题的方法有:降维,局部搜索,代理建模,分治法等。
1.2 算法背景
分解策略是一种解决高维问题比较常用的策略,它将高维问题分解为一系列规模较小并且简单的子问题,每个子问题以迭代的方式进行优化。在演化算法中,协同演化利用了高维问题的模块化特性而被广泛应用,但是在协同演化的算法中,一个主要的困难在于如何对问题进行正确的划分。在理想情况下,一个给出的目标函数,划分出的子集相互之间应该交互最小化,在黑盒问题中,交互信息无法使用,所以需要特定的算法来识别决策变量的底层交互结构。
本问题中介绍的算法是对差分分组 (DG) 算法的改进,DG 算法在 2.2 中介绍,DG 算法可以识别连续的目标函数中交互成分,并且在 CEC 2010 大规模优化问题中取得了较好的结果,然而在 CEC 2013 大规模优化问题中表现较差,其缺点如下:
-
在完全可分的函数中,消耗过多的评估次数,计算成本高;
-
无法检测具有重叠组件的目标函数,即多个组件共享决策变量;
-
对于计算舍入误差敏感;
-
要求用户指定阈值参数 (
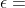 ).
).
二、算法介绍
2.1 问题介绍
分解策略利用的是函数自身的性质,这需要目标函数的可分性结构为特征,定义如下:
定义1: 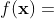 是具有
是具有 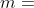 个独立组件的部分可分函数,当且仅当
个独立组件的部分可分函数,当且仅当
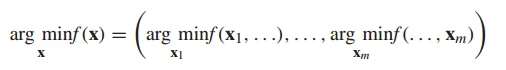
成立,其中 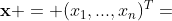 是
是 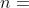 维决策变量,
维决策变量, 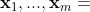 是
是 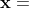 中的不相交的子向量,且
中的不相交的子向量,且 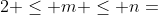 .
.
加性可分是部分可分的一种特殊形式,其定义如下:
定义2: 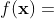 是部分加性可分函数,如果它满足下述形式
是部分加性可分函数,如果它满足下述形式
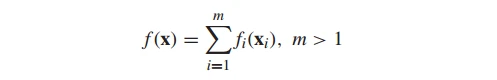
其中,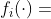 是一个不可分的子函数,
是一个不可分的子函数,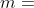 是不可分子函数的个数。
是不可分子函数的个数。
2.2 DG 算法介绍
DG 算法使用函数本身的性质来检测变量之间的交互,使用的定理如下,
定理1: 令 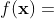 是一个加性可分函数,
是一个加性可分函数,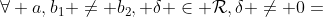 , 变量
, 变量 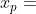 和
和 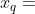 交互, 如果满足一下条件:
交互, 如果满足一下条件:
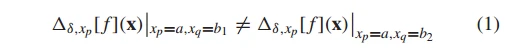
其中:
![]()
表示函数 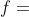 在变量
在变量 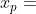 和间隔
和间隔 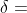 上的正向差。
上的正向差。
等式 (1) 可以简写为 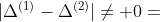 ,其中,
,其中,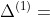 表示等式 (1) 左边,
表示等式 (1) 左边, 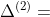 表示等式 (2) 右边。在计算机中,浮点数是没有办法做等式判断,所有上述公式需要改写成
表示等式 (2) 右边。在计算机中,浮点数是没有办法做等式判断,所有上述公式需要改写成 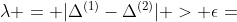 。因此,DG 算法需要通过控制参数
。因此,DG 算法需要通过控制参数 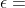 来提高算法检测的灵敏度。
来提高算法检测的灵敏度。
2.3 DG2 算法介绍
DG2 算法包括了三个部分:
1. 生成原始交互结构矩阵 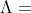 ;包含了所有变量对的值
;包含了所有变量对的值 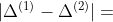 .
.
2. 找到最合适的阈值 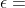 ,将原始交互结构矩阵
,将原始交互结构矩阵 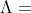 转换成设计结构矩阵
转换成设计结构矩阵 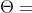 ,DG2 的阈值是不用指定的。
,DG2 的阈值是不用指定的。
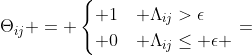
3. 根据节点连接矩阵 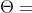 将变量分解成不可分组。
将变量分解成不可分组。
2.4 DG2 对 DG 算法的分组效率的改进
对于一个 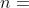 维问题,需要检查所有交互的变量对,那么总的次数为
维问题,需要检查所有交互的变量对,那么总的次数为 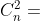 ,根据定理 1,每一次的检测需要评估四个点,所有需要总共
,根据定理 1,每一次的检测需要评估四个点,所有需要总共 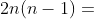 次评估次数。
次评估次数。
而事实上,我们可以大大减少这种评估次数,因为点是可以重用的。首先,我们假定一个三维问题 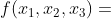 . 根据定理 1,全部的函数评估如下:
. 根据定理 1,全部的函数评估如下:
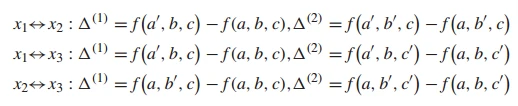
其中, 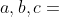 是
是 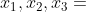 上的点,
上的点,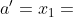 。
。
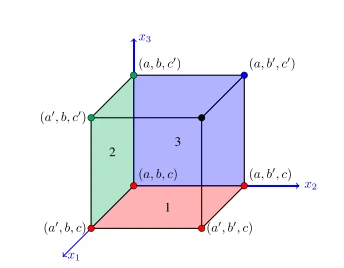
上述点的选取可以在上图中直观显示。我们只取了 7 个点便完成了这次操作,而不用取 12 个点。这其中,点 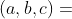 重用了 3 次,点
重用了 3 次,点 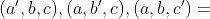 重用了 2 次。
重用了 2 次。
对上述情况可以推广到更一般的情形:

于是,总的冗余评估次数为(证明见原文):
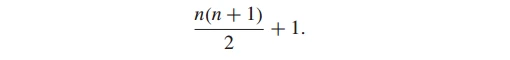
2.5 DG2 对 DG 算法的分组精确性的改进
在2.2中,提到的分组精确度依赖于阈值 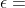 的设置,理论上,当
的设置,理论上,当 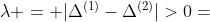 时, 变量之间就会存在交互,因此,
时, 变量之间就会存在交互,因此,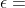 应该被设置为0. 但是,在实际中的浮点数操作中,总是会产生舍入误差,这会导致当
应该被设置为0. 但是,在实际中的浮点数操作中,总是会产生舍入误差,这会导致当 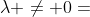 时,是因为计算误差导致的。对于 DG 算法的任务在于区别非零值
时,是因为计算误差导致的。对于 DG 算法的任务在于区别非零值 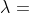 是因为出现了变量交互还是计算错误。
是因为出现了变量交互还是计算错误。
CEC2013 中的问题相较于 CEC2010 的一个区别在于每个组件的权重值是不一样的, 因此在当阈值 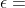 为静态时,会显著影响分组的精确性,需要一个合适的策略来自动确定阈值。
为静态时,会显著影响分组的精确性,需要一个合适的策略来自动确定阈值。
DG2 算法不采用唯一的静态阈值 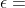 来度量分组是否出现交互,取而代之的时估算机器舍入误差的最大下界
来度量分组是否出现交互,取而代之的时估算机器舍入误差的最大下界 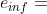 和最小上界
和最小上界 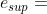 ,当
,当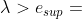 时认为两组变量是交互的,而当
时认为两组变量是交互的,而当 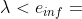 时, 认为变量时可分的。换句话说,DG2 定义了一个安全间隔来区别真正的0和非零的
时, 认为变量时可分的。换句话说,DG2 定义了一个安全间隔来区别真正的0和非零的 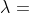 。而在上界和下界之间的这段区域,算法通过计算真实0和非零值出现的比例来近似估计这个区域中的值的所属。
。而在上界和下界之间的这段区域,算法通过计算真实0和非零值出现的比例来近似估计这个区域中的值的所属。
(1) 原理
1. 浮点数表示的误差:
根据 IEEE 754 标准, 实数 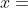 映射到浮点数
映射到浮点数 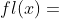 会强制进行四舍五入到最近的可表示的数。而表示的误差是
会强制进行四舍五入到最近的可表示的数。而表示的误差是 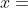 自身的函数:
自身的函数:
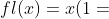
其中,边界 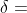 是机器相关的常数决定的,称为 machine epsilon(
是机器相关的常数决定的,称为 machine epsilon(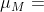 ),且
),且 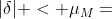 . 从上述公式中可以看出,误差项
. 从上述公式中可以看出,误差项 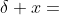 会随着
会随着 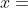 的增加而增加,在 CEC2013 问题中,处理的数字通常很大,因此,在估计阈值
的增加而增加,在 CEC2013 问题中,处理的数字通常很大,因此,在估计阈值 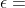 时, 需要考虑函数值的量级。
时, 需要考虑函数值的量级。
2. 浮点数计算的误差:
在 IEEE 标准中,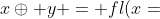 , 其中
, 其中 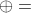 表示浮点数求和算子(其他的浮点数操作也是类似的表示)。即,两个数字的浮点和等于最接近两个数字的实数和的浮点数。这具有一般性,可以推广到如减法、乘法、除法,有时也使用于平方根的计算。但是不适用于连续的浮点计算,如
表示浮点数求和算子(其他的浮点数操作也是类似的表示)。即,两个数字的浮点和等于最接近两个数字的实数和的浮点数。这具有一般性,可以推广到如减法、乘法、除法,有时也使用于平方根的计算。但是不适用于连续的浮点计算,如 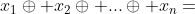 .
.
3. 上界和下界的推导:
在计算舍入误差的最大下界时,假定 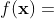 是正确的, 唯一的错误来源于
是正确的, 唯一的错误来源于 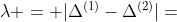

在上式中, 误差来源于 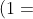 的二次乘积 (
的二次乘积 (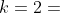 ,
,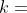 表示误差迭代的指数),因此有如下推导:
表示误差迭代的指数),因此有如下推导:
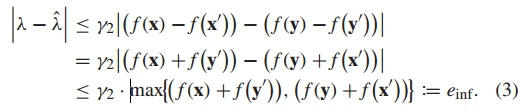
在等式 (3) 中,我们假设函数值域是非负的,更一般的情况有:
![]()
估算舍入误差的上界时,需要考虑函数计算的误差。而由于函数是黑盒的,我们无法得知误差项 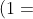 在
在 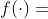 中的准确值, 根据经验法则的分析,通常假设误差随着计算过程中浮点操作次数 (
中的准确值, 根据经验法则的分析,通常假设误差随着计算过程中浮点操作次数 (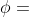 ) 的平方根增长。综上,我们假定
) 的平方根增长。综上,我们假定 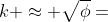 ,同时,假定
,同时,假定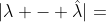 的计算误差相对于
的计算误差相对于 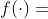 而言是可以忽略的,于是,上界的定义如下:
而言是可以忽略的,于是,上界的定义如下:
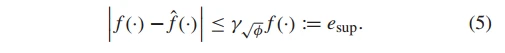
在等式 (5) 中,我们无法知道浮点操作次数 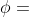 ,为了处理这种问题,我们假设问题维度
,为了处理这种问题,我们假设问题维度 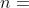 和浮点操作数
和浮点操作数 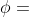 具有相关性。通常,
具有相关性。通常,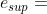 值过高会使得对相互变量的检测精度较高,这会忽略一些相互作用的变量,而
值过高会使得对相互变量的检测精度较高,这会忽略一些相互作用的变量,而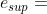 值较低的话,则分组会多一些不交互的变量,但是这并不会产生有害的结果,因此可以假定问题维度
值较低的话,则分组会多一些不交互的变量,但是这并不会产生有害的结果,因此可以假定问题维度 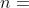 和浮点操作数
和浮点操作数 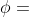 具有线性复杂度,定义如下:
具有线性复杂度,定义如下:
![]()
4. 动态阈值的设定
在 3 中计算了阈值的上界和下界,在区间 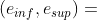 中的值通过使用边界加权动态设定:
中的值通过使用边界加权动态设定:
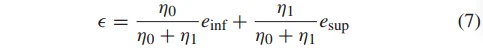
其中 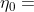 是所有检测的变量对中小于
是所有检测的变量对中小于 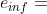 的个数,
的个数,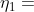 是所有检测的变量对中大于
是所有检测的变量对中大于 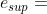 的个数。
的个数。
[1] Omidvar M N, Yang M, Mei Y, et al. DG2: A faster and more accurate differential grouping for large-scale black-box optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(6): 929-942.
