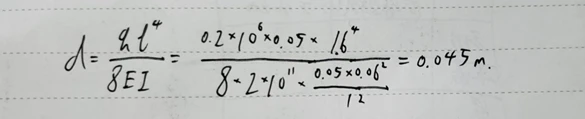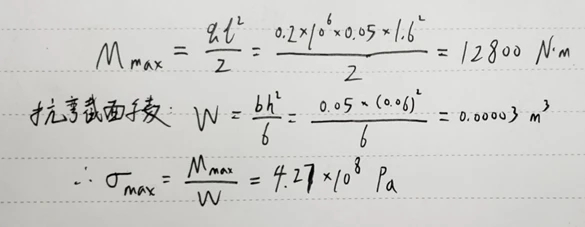1. 摘要
对于矩形悬臂梁均布载荷问题,分别采用不同单元模型进行分析,对比考察分析结果的差异。
2. 问题描述
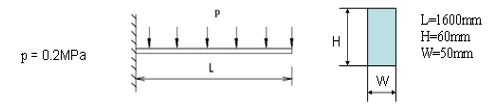
如图所示矩形截面悬臂梁,左端固定,材料为钢。材料参数为:弹性模量E=2E11Pa,泊松比u=0.28,密度ρ=7800kg/m^3。几何参数如图中所示。梁上作用有均布载荷。
分别采用三维实体单元、平面应力单元及梁单元进行分析;对比考察梁右端的位移和左端的应力分布;讨论理论计算值与有限元计算结果差异。
3. 技术路线
此问题属于结构分析范畴,借助ANSYS Mechanical APDL模块,通过软件界面操作方式实现。单位制:m、kg、s、N、Pa。
分别采用三维实体单元Brick 8 node 185、平面应力单元Quad 4 node 182及梁单元2 node 188进行分析。
4. 分析过程
4.1 三维实体单元分析
(一) 定义工作文件名
依次单击Utility Menu>File>Change Jobname,在出现的对话框中输入:beam,在“New Log and error files”处选中“yes”,单击“OK”。
(二) 定义单元类型
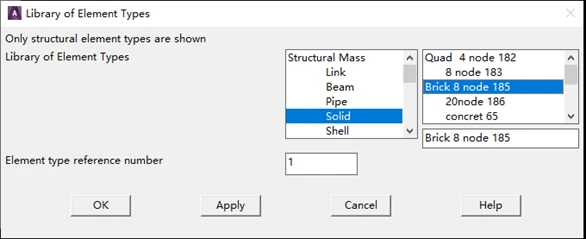
- 依次单击 MainMenu>Preprocessor>Element type>Add/Edit/Delete,出现对话框,单击“Add”,出现一个 “Library of Element Type”对话框。在“Library of Element Type”左面的列表栏中选择“Solid”,在右面的列表栏中选择“Brick 8 node 185”,单击“OK”。
(三) 设置材料属性
依次单击Main Menu>Preprocessor>Material Props>Material Models,出现“Define Material Model Behavior”对话框,在“Material Model Available”下面的对话框中,双击打开“Structural>Linear>Elastic>Isotropic”,出现对话框,输入弹性模量EX=2e11,泊松比PRXY=0.28,单击“OK”,单击“Material>Exit”。
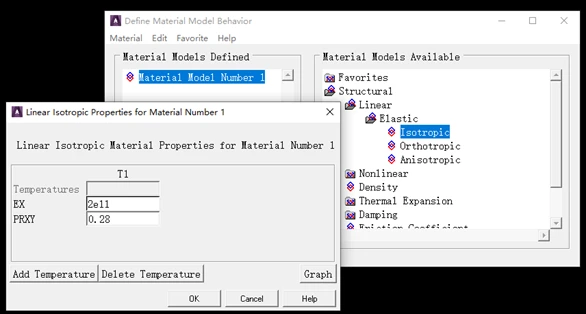
(四) 建立几何模型
- 创建长方体
拾取菜单 Main Menu>Preprocessor>Modeling>Create>Volumes>Block> By Dimensions。弹出如下图所示的对话框,在“X1,X2” 文本框中输入 0,1.6,在“Y1,Y2”文本框中输入 0,0.05, 在“Z1,Z2” 文本框中输入 0,0.06,单击 OK。
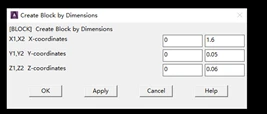

(五) 划分单元
- 拾取菜单Main Menu>Mesh>Mesh Tool。弹出对话框,在 Mesh 选项中选择Volums,在 Shape 选项中选择 Hex 和 Mapped,然后点下方的 Mesh,即可划分好。

(六) 施加载荷和边界条件
- MainMenu>Solution>DefineLoads>Apply>Structural>Displacement>On Areas,拾取左端面,然后点击OK。并在弹出的对话框里选择 All DOF,点击 ok。
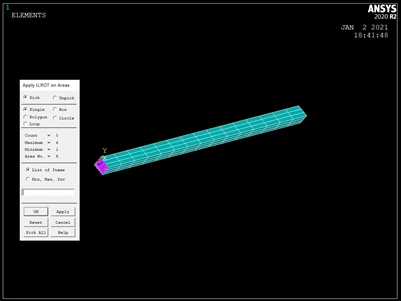
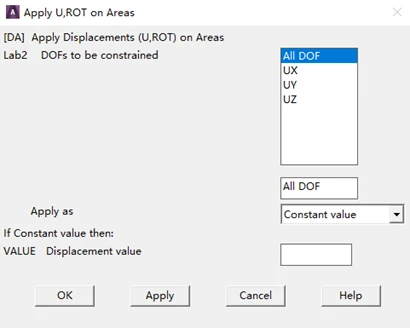
- 选择 MainMenu>Solution>DefineLoads>Apply>Structural>pressure>On Areas,拾取上端面,点击 OK。在弹出的对话框中输入200000。


(七) 求解模型
依次点击Main Menu>Solution>Solve>Current LS进行求解,当提示Solution is Done说明求解完成。
(八) 结果查看
依次单击Main Menu>GeneralPostproc>PlotResults>Contour Plot>Nodal Solu,弹出对话框,在“Item to be Contoured”栏中选择“Stress”,在其右面的栏中,选择“von Mises stress”后,单击“OK”,这时在图形窗口处显示出平面的应力云图,如图所示。
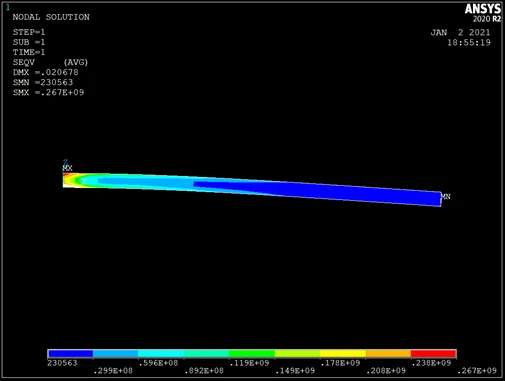
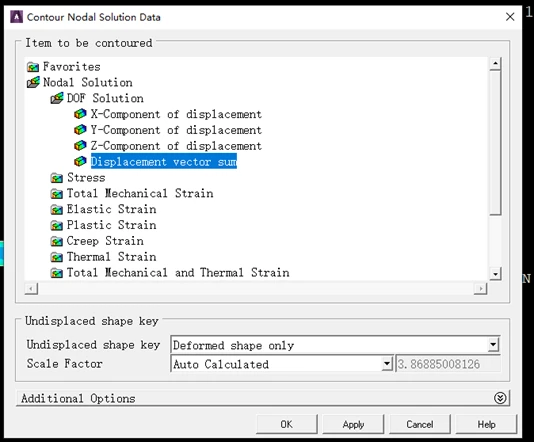
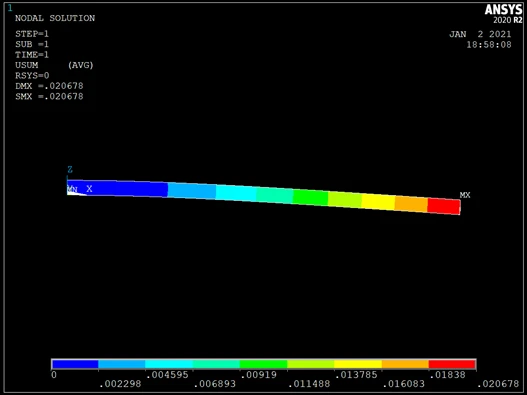
依次单击 Main Menu>GeneralPostproc>Plot Results>Contour Plot>Nodal Solu,弹出对话框,在“Item to be Contoured”栏中选择“DOF Solution”,在其右面的栏中,选择“Displacement vector sum”后,单击“OK”,这时在图形窗口处显示出三维应变图,如图所示。
4.2 平面应力单元分析
(一) 定义工作文件名
依次单击Utility Menu>File>Change Jobname,在出现的对话框中输入:beam,在“New Log and error files”处选中“yes”,单击“OK”。
(二) 定义单元类型
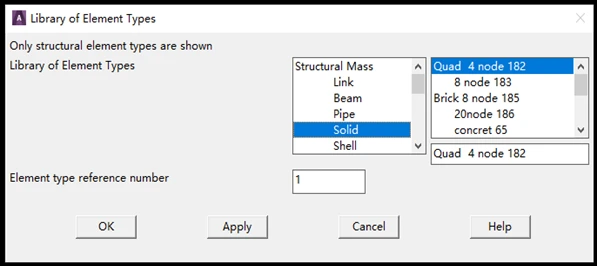
- 依次单击 MainMenu>Preprocessor>Element type>Add/Edit/Delete,出现对话框,单击“Add”,出现一个 “Library of Element Type”对话框。在“Library of Element Type”左面的列表栏中选择“Solid”,在右面的列表栏中选择“Quad 4 node 182”,单击“OK”。
(三) 设置材料属性
依次单击Main Menu>Preprocessor>Material Props>Material Models,出现“Define Material Model Behavior”对话框,在“Material Model Available”下面的对话框中,双击打开“Structural>Linear>Elastic>Isotropic”,出现对话框,输入弹性模量EX=2e11,泊松比PRXY=0.28,单击“OK”,单击“Material>Exit”。

(四) 建立几何模型
- 创建长方形
拾取菜单MainMenu>Preprocessor>Modeling>Create>Areas>Rectangle>By 2 Corners。弹出如下图所示对话框,Width填入1.6,Height填入0.06。点击OK。


(五) 划分单元
- 拾取菜单 Main Menu>Mesh>Mesh Tool。在 Mesh 选项中选择 Lines旁边的 set,分别划分两条长边为 15 份,两条短边为 3 份;然后点击最下方的mesh,选择矩形,点击 OK。

(六) 施加载荷和边界条件
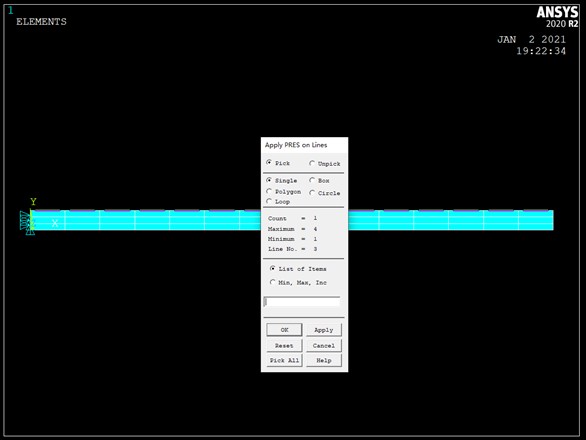
- MainMenu>Solution>DefineLoads>Apply>Structural>Displacement>On Lines,拾取左端线,然后点击OK。并在弹出的对话框里选择 All DOF,点击 ok。
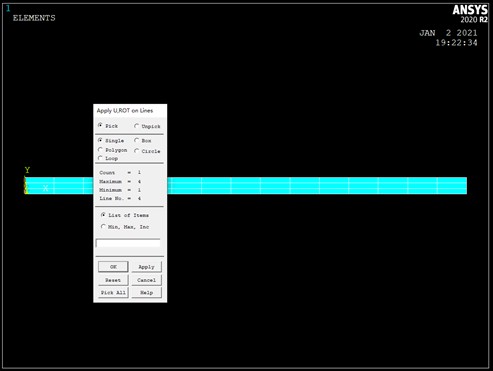

- 选择 MainMenu>Solution>DefineLoads>Apply>Structural>
pressure>On Lines,拾取上端线,点击 OK。在弹出的对话框中输入200000。


(七) 求解模型
依次点击Main Menu>Solution>Solve>Current LS进行求解,当提示Solution is Done说明求解完成。
(八) 结果查看
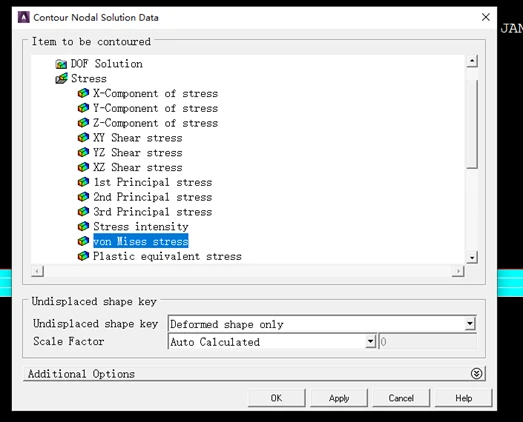
依次单击Main Menu>GeneralPostproc>PlotResults>Contour Plot>Nodal Solu,弹出对话框,在“Item to be Contoured”栏中选择“Stress”,在其右面的栏中,选择“von Mises stress”后,单击“OK”,这时在图形窗口处显示出平面的应力云图,如图所示。
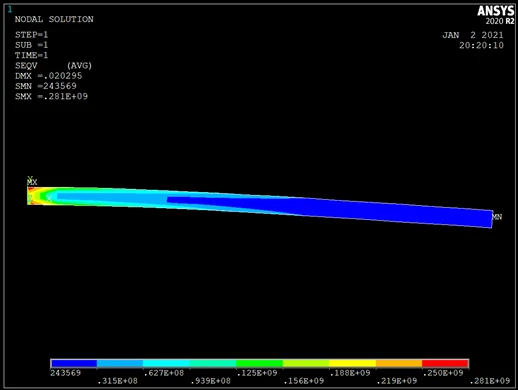
依次单击 Main Menu>GeneralPostproc>Plot Results>Contour Plot>Nodal Solu,弹出对话框,在“Item to be Contoured”栏中选择“DOF Solution”,在其右面的栏中,选择“Displacement vector sum”后,单击“OK”,这时在图形窗口处显示出三维应变图,如图所示。
4.3 梁单元分析
(一) 定义工作文件名
依次单击Utility Menu>File>Change Jobname,在出现的对话框中输入:beam,在“New Log and error files”处选中“yes”,单击“OK”。
(二) 定义单元类型
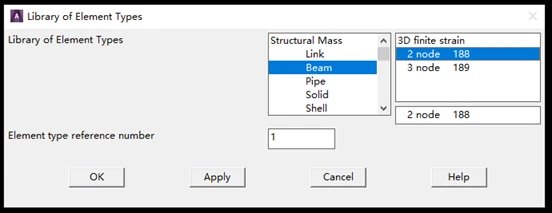
- 依次单击 MainMenu>Preprocessor>Element type>Add/Edit/Delete,出现对话框,单击“Add”,出现一个 “Library of Element Type”对话框。在“Library of Element Type”左面的列表栏中选择“Beam”,在右面的列表栏中选择“2 node 188”,单击“OK”。
(三) 设置材料属性
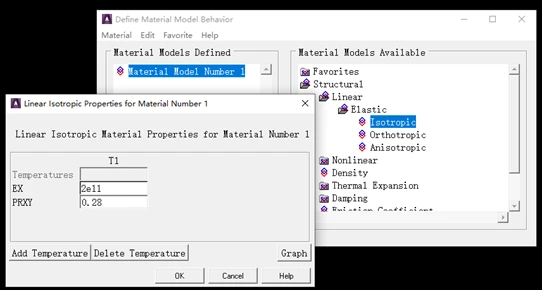
依次单击Main Menu>Preprocessor>Material Props>Material Models,出现“Define Material Model Behavior”对话框,在“Material Model Available”下面的对话框中,双击打开“Structural>Linear>Elastic>Isotropic”,出现对话框,输入弹性模量EX=2e11,泊松比PRXY=0.28,单击“OK”,单击“Material>Exit”。
(四) 建立几何模型
- 创建直线
创建关键点1(0,0,0)和关键点2(1.6,0,0),再创建关键点 10(0,1, 0),这是截面的方向点。然后连接点 1 和 2 形成直线。

- 定义截面属性
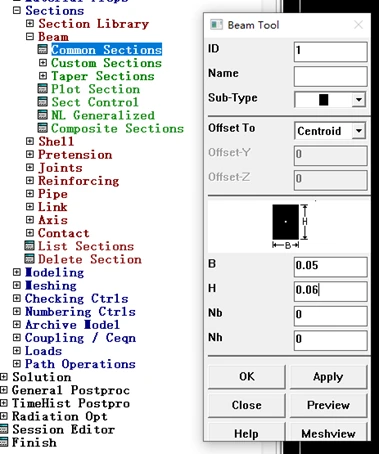
(五) 划分单元
- 打开 Mesh tool,在上面的 set 中选 line;选择关键点 10 为截面方向点,选好之后点击中间 line 后的 set,划分成15份,然后点击最底下的 mesh,选择直线,点击 OK。
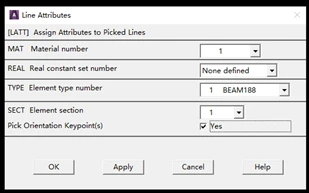

(六) 施加载荷和边界条件
- 对左端点施加全约束载荷。
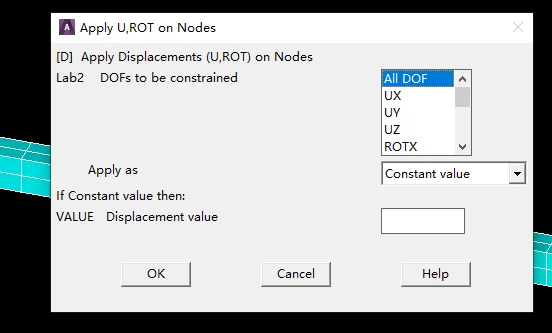

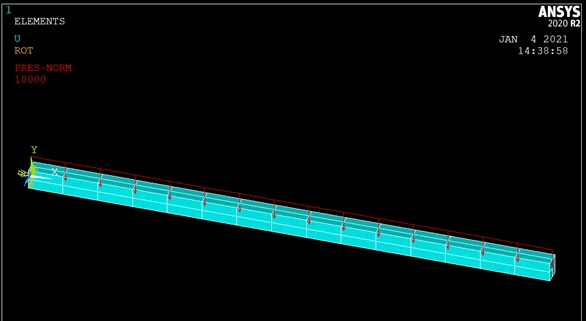
- 选择 MainMenu>Solution>DefineLoads>Apply>Structural>pressure>On Beams,框选整根梁。

由于载荷作用在y轴负方向,因此在弹出窗口的第一个空中输入1,由于需要将题目中的均布在面上的载荷转换为均布在线上的载荷,因此第二个以及第三个空中输入10000(200000*0.05)。
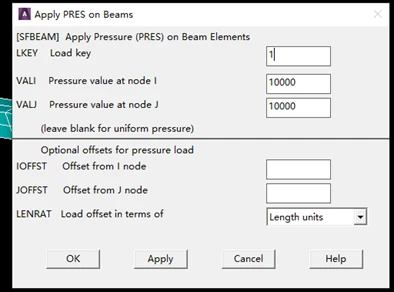
(七) 求解模型
依次点击Main Menu>Solution>Solve>Current LS进行求解,当提示Solution is Done说明求解完成。
(八) 结果查看
依次单击Main Menu>GeneralPostproc>PlotResults>Contour Plot>Nodal Solu,弹出对话框,在“Item to be Contoured”栏中选择“Stress”,在其右面的栏中,选择“von Mises stress”后,单击“OK”,这时在图形窗口处显示出平面的应力云图,如图所示。
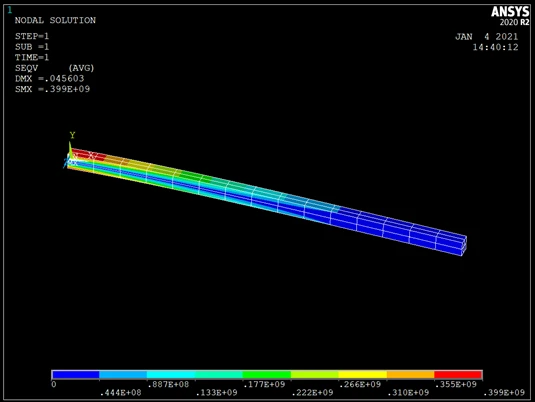
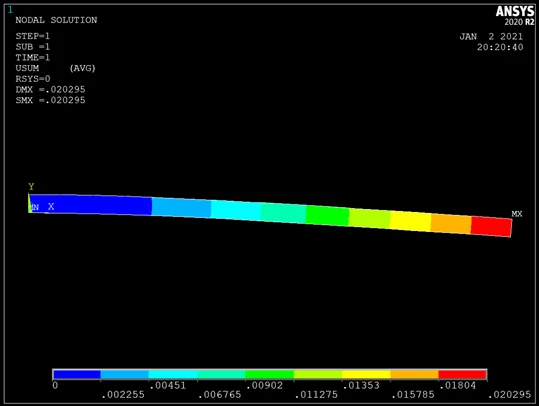
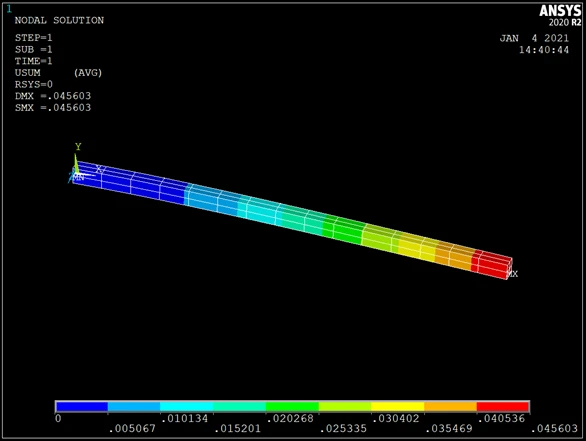
依次单击 Main Menu>GeneralPostproc>Plot Results>Contour Plot>Nodal Solu,弹出对话框,在“Item to be Contoured”栏中选择“DOF Solution”,在其右面的栏中,选择“Displacement vector sum”后,单击“OK”,这时在图形窗口处显示出三维应变图,如图所示。
5. 结果和讨论
有限元计算结果与理论计算值的对比如下表所示。
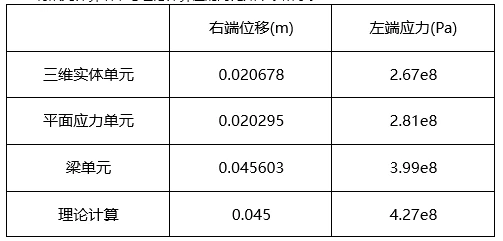
由表可以看出,采用三维实体单元与平面应力单元进行分析,得到的结果与理论计算结果相差较大,采用梁单元分析得到的结果与理论计算结果相差较小。产生的误差可能是由于模型误差导致的。
因此可得出结论,采用梁单元进行分析,与理论计算结果的差异更小。
附:理论计算过程