假设一个集合包含n个元素,要求计算该集合的子集个数。
该集合的所有子集,也叫该集合的幂集,比如集合{1,2,3}的所有子集为 空集,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}数一数,一共8个,由此推测为2的三次方,即2的三次幂。那么这个结论是否正确呢?
方法1:
一共集合有n个元素,它的子集的个数就是对这n个元素做组合,一共有n个位置可以组合,每个位置上该元素可以出现也可以不出现,所以最后总的个数为2的n次方。
方法2:
具有n个元素的集合的子集其实就是空集,含有一个元素的集合,含有两个元素的集合...含有n个元素集合,这集合的和就是,如图1所示。
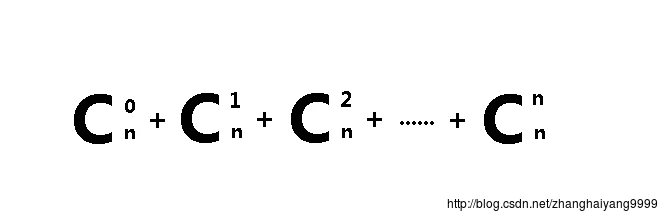
根据多项式的公式和定理知道,上面式子之和为2的n次方。
