目录
6-1 分类
6-2 假设陈述
6-3 决策界限
6-4 代价函数
6-5 简化代价函数与梯度下降
6-6 高级优化
6-7 多元分类
6-1 分类
主要考虑离散系统,如分类问题:
例1:垃圾邮件分类
例2:欺诈网站判断
例3:肿瘤良/恶性分类
设y∈{0,1} (其中0表示正面分类,1表示负面分类)
例:肿瘤分类问题,1表示恶性,0表示良性

用直线h_Θ(x)=Θ^T*x对数据进行拟合
设置阈值为0.5,若h_Θ(x)≥0.5,预测y=1;若h_Θ(x)≤0.5,预测y=0。
但若延长横轴,并在训练集内增加一个位于横轴较右端的元素,此时阈值仍设0.5,得到的拟合曲线如图
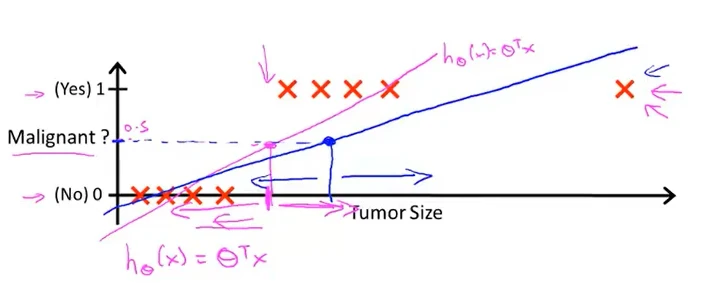
此时得到的结果并不理想,因为拟合直线左边的恶性肿瘤被认为是良性的。因此,线性回归并不适用于分类问题,因此使用logistic回归。
6-2 假设陈述
我们需要0≤h_Θ(x)≤1,即使用logistic回归模型
logistic回归:h_Θ(x)=g(Θ^T*x)
z=Θ^T*x
g(Z)=1/(1+e^-z) (logistic函数)
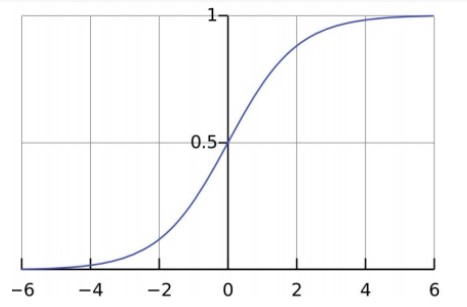
可以使用概率论描述可能得到的结果:
hθ(x)=P(y=1|x;θ)=1−P(y=0|x;θ)
P(y=0|x;θ)+P(y=1|x;θ)=1
6-3 决策界限
若:
hθ(x)≥0.5→y=1
hθ(x)<0.5→y=0

由图像及函数可得:当z≥0时,g(z)≥0.5。因此只需满足Θ^T*x≥0,就求得hθ(x)≥0.5
1.线性决策边界
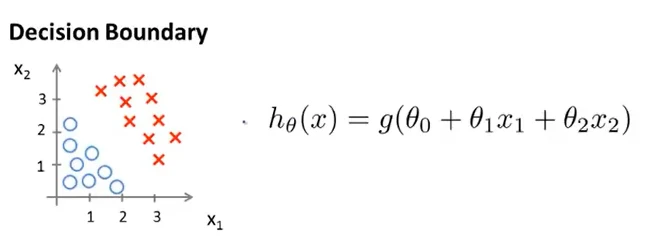
设Θ=[-3;1;1],当-3+x1+x2≥0时,y=1。
-3+x1+x2≥0曲线将左图上分为两部分,该曲线称为决策边界。
2.非线性决策边界
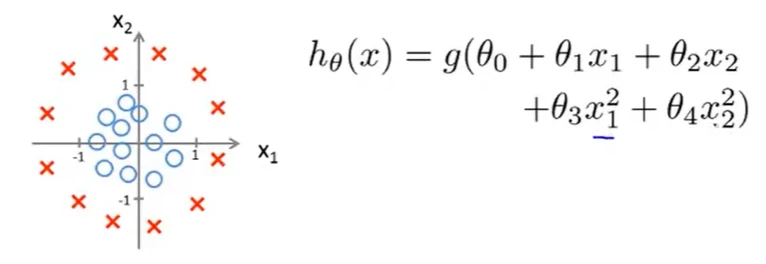
θ=[-1;0;0;1;1],当-1+(x_1)^2+(x_2)^2≥0时,y=1
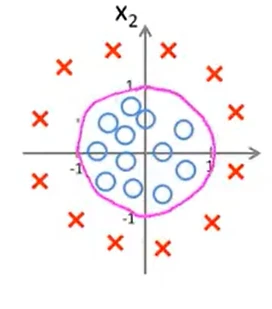
决策边界如上图所示
6-4 代价函数
下面讨论监督学习中的分类问题:
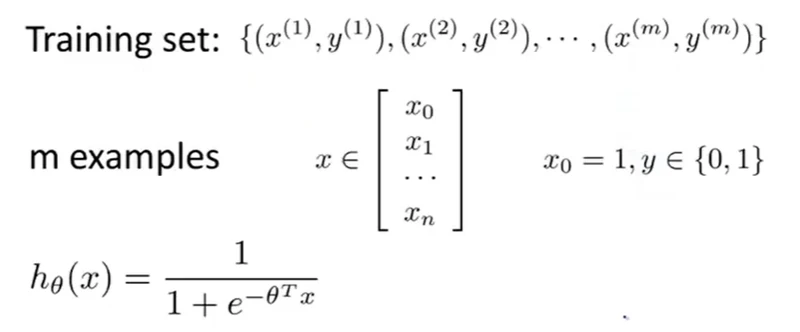
如何选择Θ?
代价函数:
![]()
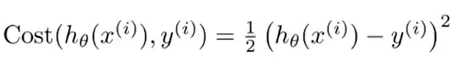
但如果应用这个代价函数,生成的目标函数图像为非凸曲线,该曲线上有很多局部最优点,因此无法使梯度下降法很好的工作。
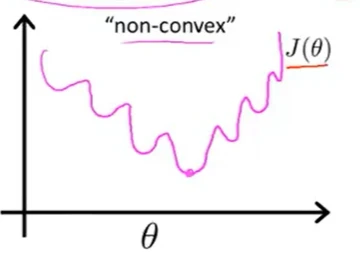
因此使用logistic回归代价函数:
Cost(hθ(x),y)=−log(hθ(x))) if y = 1
Cost(hθ(x),y)=−log(1−hθ(x)) if y = 0
得到图如下:
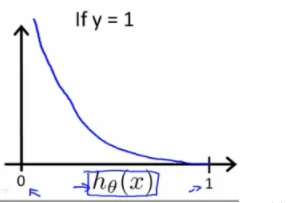
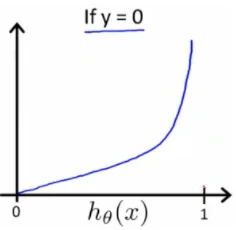
性质:
Cost(hθ(x),y)=0 if hθ(x)=y
Cost(hθ(x),y)→∞ if y=0andhθ(x)→1
Cost(hθ(x),y)→∞ if y=1andhθ(x)→0
6-5 简化代价函数与梯度下降
将上一节的logistic代价函数简化
Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
代价函数如下:
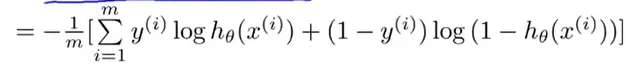
使用梯度下降法,最小化代价函数J(θ)

6-6 高级优化
在计算代价函数及其偏导数后可以选用梯度下降法计算θ,但梯度下降法并非唯一的算法,一些高级优化算法包括:共轭梯度法、BFGS(拟牛顿法 )、L-BFGS。这些高级优化算法不需要手动寻找学习率且通常快于梯度下降法。
举例:
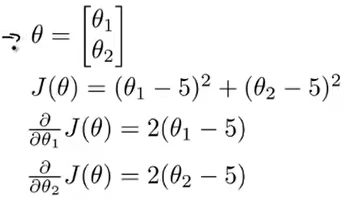
利用高级优化算法
function [jVal,gradient]=costFunction(theta) %jVal代价函数,gradient梯度变量
jVal=(theta(1)-5)^2+(theta(2)-5)^2;
gradient=zeros(2,1);
gradient(1)=2*(theta(1)-5);
gradient(2)=2*(theta(2)-5);>> options=optimset('GradObj','on','MaxIter',100); % 设置梯度目标打开,设置迭代次数
>> initialTheta=zeros(2,1) % θ猜测值
>> [optTheta,functionVal,exitFlag]=fminunc(@costFunction,initialTheta,options)
optTheta =
5
5
functionVal =
0
exitFlag = %收敛标志
1在使用时,initialTheta值必须是d维的(d≥2)
将其应用于logistic回归中:

6-7 多元分类
当我们需要将一组数据按照不特征进行分类,即多元分类。例如下图所示的数据集;

我们可以将这一问题转化为二元分类问题,即首先将“三角形”作为独立的一类,剩下所有数据作为一类,进行分类。如图所示:
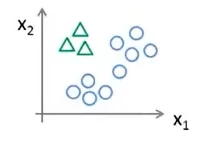
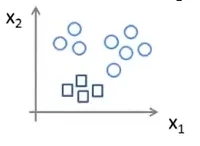
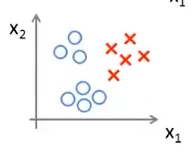
可以得到三个拟合曲线,最后我们输入一个新的x,选择分类器最大的那个输出即是y
