一:什么是MRO
所谓的MRO,就是方法解析顺序(Method Resolution Order)。在调用方法时,会对当前类以及所有的基类进行一个搜索,确定要调用的方法具体在哪。不管用哪种方式去确定MRO列表,必须满足 本地优先级和单调性。
本地优先级:指声明时父类的顺序,比如C(A,B),如果访问C类对象属性时,应该根据声明顺序,优先查找A类,然后再查找B类
单调性:如果在C的解析顺序中,A排在B的前面,那么在C的所有子类里,也必须满足这个顺序
二:常见的mro算法
1:mro=深度优先遍历的(DFS)
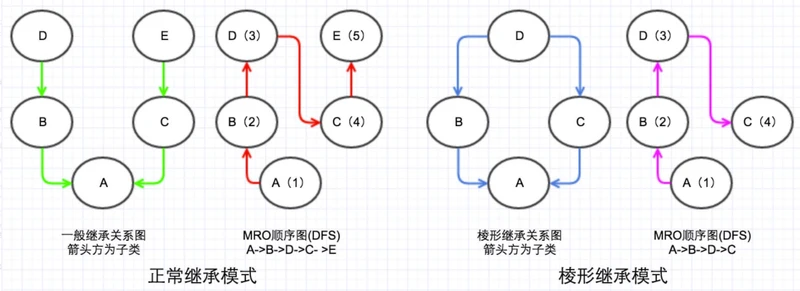
正常继承模式 没有任何问题。。。
菱形继承模式 就有问题啦。。
比如说C重写了D中的test()方法,A在调用test()时,按照MRO顺序调用的是D中的test,此时C中重写的test()方法将永远访问不到,导致了C只能继承不能重写D中的方法(即使C重写了test()方法也不会访问到),这就是DFS的缺陷。
2:mro=广度优先遍历的(BFS)
既然采用DFS存在问题,采用BFS会不会就没有上边的问题尼?
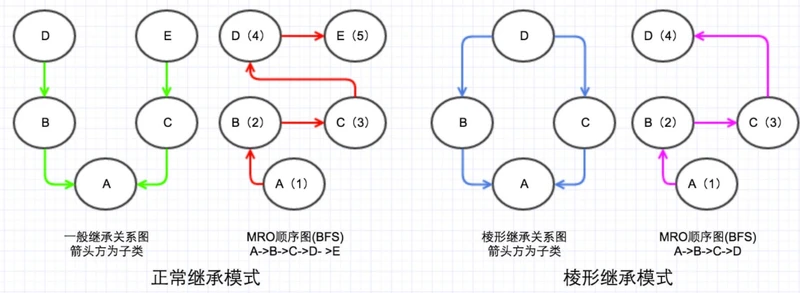
正常继承模式 有问题啦
比如说 C D中都有test()方法,A中调用test()按照MRO顺序 调用到了C中的test(),这显然是不正确的,因为先从B开始搜索 B中虽然没有 但是B的父类D中有,正常应该调用D中的test()。所以如果采用BFS时,正常继承模式 不满足前边说的单调性。。
菱形继承模式 没有问题,解决了DFS菱形继承带来的问题
3:mro=C3算法
既然DFS和BFS都存在问题,那么只能才用其他方式了,这就是C3啦。。。
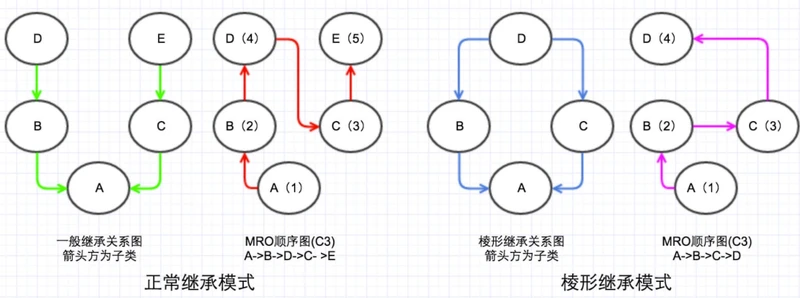
正常继承模式和菱形继承模式 都没有问题,DFS和BFS存在的问题都给解决了,哈哈 是不是很棒
正常继承
class D(object):
def __init__(self):
super(D,self).__init__()
print('D')
def fun(self):
print('D fun()')
class E(object):
def __init__(self):
super(E,self).__init__()
print('E')
class C(E):
def __init__(self):
super(C,self).__init__()
print('C')
def fun(self):
print('C fun()')
class B(D):
def __init__(self):
super(B,self).__init__()
print('B')
class A(B,C):
def __init__(self):
super(A,self).__init__()
print('A')
if __name__ == '__main__':
a = A()
print(A.__mro__)
a.fun()菱形继承
class D(object):
def __init__(self):
super(D,self).__init__()
print('D')
def fun(self):
print('D fun()')
class C(D):
def __init__(self):
super(C,self).__init__()
print('C')
def fun(self):
print('C fun()')
class B(D):
def __init__(self):
super(B,self).__init__()
print('B')
class A(B,C):
def __init__(self):
super(A,self).__init__()
print('A')
if __name__ == '__main__':
a = A()
print(A.__mro__)
a.fun()

| 算法 | 正常继承 mro顺序 | 菱形继承 mro顺序 |
|---|---|---|
| DFS | A,B,D,C,E | A,B,D,C (只能继承,不能重写问题) |
| BFS | A,B,C,D,E(不满足单调性原则) | A,B,C,D |
| C3 | A,B,D,C,E | A,B,C,D |
三:C3算法
C3算法的核心就是merge
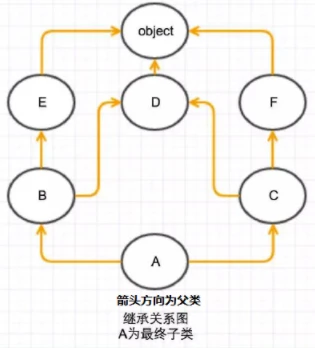
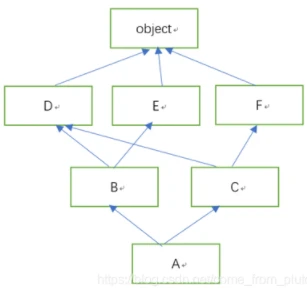
利用merge计算A的mro (O代表object类)
mro(E) = [E,O]
mro(D) = [D,O]
mro(F) = [F,O]
mro(B) = [B] + merge(mro(E),mro(D),[E,D])
= [B] + merge([E,O],[D,O],[E,D]) E符合merge条件
= [B,E] + merge([O],[D,O],[D]) D符合merge条件
= [B,E,D] + merge([O],[O],[]) O符合merge条件
= [B,E,D,O]
mro(C) = [C] + merge(mro(D),mro(F),[D,F])
= [C] + merge([D,O],[F,O],[D,F]) D符合merge条件
= [C,D] + merge([O],[F,O],[F]) F符合merge条件
= [C,D,F] + merge([O],[O],[]) O符合merge条件
= [C,D,F,O]
mro(A) = [A] + merge(mro(B),mro(C),[B,C])
= [A] + merge([B,E,D,O] ,[C,D,F,O] ,[B,C]) B符合merge条件
= [A,B] + merge([E,D,O] ,[C,D,F,O] ,[C]) E符合merge条件
= [A,B,E] + merge([D,O] ,[C,D,F,O] ,[C]) C符合merge条件
= [A,B,E,C] + merge([D,O] ,[D,F,O] ,[]) D符合merge条件
= [A,B,E,C,D] + merge([O] ,[F,O] ,[]) F符合merge条件
= [A,B,E,C,D,F] + merge([O] ,[O] ,[]) O符合merge条件
= [A,B,E,C,D,F,O] 与程序结果一致利用拓扑排序计算mro
根据继承关系图,(简单来说就是不停找入度为0的点,然后减去相连的边,不停重复,直至只剩下一个点)
找到入度为0的点,只有A,将A加入mro顺序列表中,剪掉与A相连的边;
再找入度为0的点,有两个点B和C,取最左,so将B加入mro顺序列表中,剪掉与B相连的边;
再找入度为0的点,有两个点E和C,取最左,so将E加入mro顺序列表中,剪掉与E相连的边;
再找入度为0的点,只有C,so将C加入mro顺序列表中,剪掉与C相连的边;
再找入度为0的点,有两个点D和F,取最左,so将D加入mro顺序列表中,剪掉与D相连的边;
再找入度为0的点,只有F,so将F加入mro顺序列表中,剪掉与F相连的边;
只剩下object,将object加入mro顺序列表中;
此时得出mro = [A,B,E,C,D,F,O],与程序结果一致.class D(object):
pass
class E(object):
pass
class F(object):
pass
class B(E,D):
pass
class C(D,F):
pass
class A(B,C):
pass
print(A.__mro__)![]()
打印A的__mro__ 结果是ABECDFO 根上边分析计算的一样
变换一下 就是D和E的位置交换一下,也就是B的父类由B(E,D)--->B(D,E)
class D(object):
pass
class E(object):
pass
class F(object):
pass
class B(E,D):
pass
class C(D,F):
pass
class A(B,C):
pass
print(A.__mro__)
打印A的__mro__ 结果是ABCDEFO
变换前:A B 相连的边都剪掉后,此时入度为0的节点有C和E,这里先选的是E
变换后:A B 相连的边都剪掉后,此时入度为0的节点有C和E,这里先选的是C
四:经典类、新式类中MRO
1:经典类 mro=深度优先遍历的(DFS)
经典类没有__mro__属性
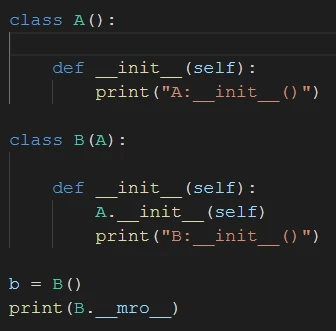
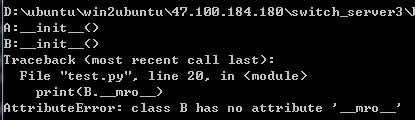
2:新式类 mro=C3算法
新式类有__mro__属性


