日历的算法

日历算法学习总结——公历

学习了日历算法，做些记录，方便以后复习。

1 历法：

公元1582年10月15日起使用格里历。

公元1582年10月4日之前到公元前45年1月1日使用儒略历。

公元前45年1月1日，历史学家、历法学者等都推荐使用儒略历法。因此计算公历时，1582年10月4日之前都使用儒略历。

历史上没有公元0年，也没有公元1582年10月5日~1582年10月14日这10天。即公元前1年（-1年）之后直接是公元1年（1年），公元1582年10月4日之后直接是公元1582年10月15日。

不管是格里历还是儒略历，1到12月份每月的天数是相同的：
平年：31、28、31、30、31、30、31、31、30、31、30、31；
闰年：31、29、31、30、31、30、31、31、30、31、30、31。
（注：儒略历在发布不久，在每月设置天数还是挺乱的，真实的并非是上面的天数。包括置闰年也是搞错一段时间。直到公元3年后才走上正轨。）

2 闰年计算：

2.1 格里历：
（1）如果年份是4的倍数，且不是100的倍数，则是闰年；
（2）如果年份是400的倍数，且不是3200的倍数，则是闰年；
（3）如果年份是86400的倍数，则是闰年；
（4）不满足（1）、（2）、（3）条件的就是平常年。

2.2 儒略历：
每4年置一闰年。
从公元1年开始算起：……-7年、-5年、-1年、4年、8年、12年、16年……即：
（1）公元前年份（用负数表示）+1是4的倍数，则是闰年；
（2）公元后年份是4的倍数，则是闰年；
（3）不满足（1）、（2）条件的就是平常年。

2.3 闰年计算函数：

/*判断是否是闰年*/
bool IsLeapYear(int year)
{
    if(year > 1582)
        /*格里历：能被4整除且不能被100整除；或者能被400整除且不能被3200整除；或者能被86400整除的年份是闰年。*/
        return((year % 4 == 0) && (year % 100 != 0) || (year % 400 == 0) && (year % 3200 != 0) || (year % 86400 == 0));

    else if((year > 0) && (year <= 1582))
        /*儒略历:1年至1582年每4年一闰*/
        return(year % 4 == 0);

    else
        /*儒略历:公元前每4年一闰*/
        return((year + 1) % 4 == 0);
}

3 获得每月天数：

平年：31、28、31、30、31、30、31、31、30、31、30、31；
闰年：31、29、31、30、31、30、31、31、30、31、30、31。

/*获得公历月天数*/
int GetDaysOfMonth(int year, int month)
{
    int daysoOfMonth[12] = {31,28,31,30,31,30,31,31,30,31,30,31};
    if((month < 1) || (month > 12))
        return 0;

    int days = daysoOfMonth[month -1];

    if ((month == 2) && IsLeapYear(year))  //如果是闰年，2月份加1天
        days++;

    return days;
}

4 计算某日是星期几：

4.1 1582年10月15日之后的计算和原理：
（1）已知某日是星期几a，求其它日是星期几w等于这两日的天数差除以7的余数b加上a ，w=b+a，如果w大于7则再一次除以7取余数（取7的模数）。
星期一到星期日用序号：1、2、3、4、5、6、0表示。

（2）两日期天数差D的计算：
为方便计算把已知的日期定为某个特定的日期。

以0年2月29日为基准，0年2月29日为星期二（按格里历反推出来的基准，并非是按儒略历算出来的真实星期），这样计算某日与0年2月29日的天数差就是某日从0年3月1日算起的天数：
D=某日期之前的年的总天数D_y+某日期在当年本月之前月的总天数D_m+某日期在本月的天数D_d。
D=D_y+D_m+D_d

因为2月有平年和闰年之分，月的天数相加比较麻烦。为了消除2月份平闰天数的影响，把1月份、2月份当作上一年的13月份、14月份，每年以3份开始14月份（2月份）结束。
即当月份month <= 2时：
month = month +2
year取上一年，year = year - 1。以下同。
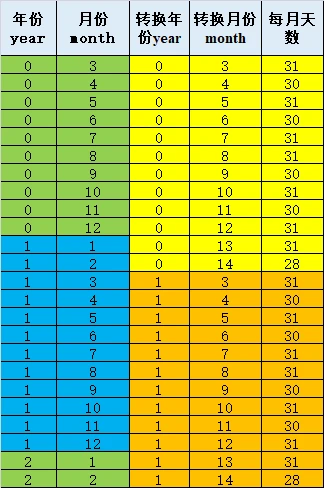
在这里插入图片描述
根据上面的方法折算，得：
某日期之前年的总天数D_y：
D_y=年数×365+闰年次数L=年份year×365+闰年次数L
D_y=year×365+L
L=[year/4]-[year/100]+[year/400]-[year/3200]+[year/86400]
（注：[ ]表示仅仅取整数部份，如 [-12.89] = -12，[0.98] = 0）
D_y=year×365+[year/4]-[year/100]+[year/400]-[year/3200]+[year/86400]

某日期在当年本月之前月的总天数D_m：
转换后每月天数：
在这里插入图片描述
D_m=31(3月)+30(4月)+31(5月)+……+某日期的上月天数
14月份（2月份）是最后的月份，在统计月份的天数时它就不会被计算在内，它只能参与计算某日期在本月的天数D_d。所以月份这样转换后消除了闰月的影响。

计算某日期在当年本月之前月的总天数D_m看下面的推算表：
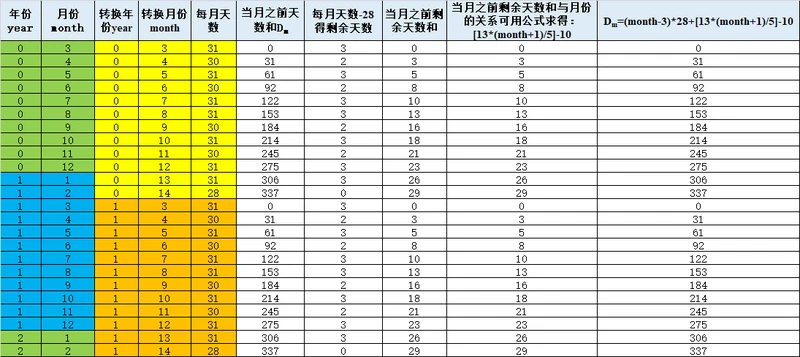
在这里插入图片描述
D_m=(month-3)×28+[13×(month+1)/5]-10

某日期在本月的天数D_d：
某日期在本月的天数D_d等于其日期day。
D_d=day

总天数D：
D=D_y+D_m+D_d
=year×365+[year/4]-[year/100]+[year/400]-[year/3200]+[year/86400]+(month-3)×28+[13×(month+1)/5]-10+day （公式1）

year为某日期的年份，如果是1月、2月，则year为上一年，year=year-1。
month为某日期的月份，如果是1月、2月，则month为13、14。以下相同。

简化公式：
计算某日是星期几w = D % 7 + 2，其中2是0月2月29日的星期二序号。
求模运算有这样的关系：
如果a=bk+c，（k、c是整数），则有a % b = c。c就余数。
如果D可表示为
D=7k+D’
则有
D ≡ D’ (mod 7）
其中，≡是数论中表示同余的符号，mod 7的意思是指在用7作模数（也就是除数）的情
况下≡号两边的数是同余的。
w = D % 7 +2 = (D + 2) % 7 = (7k + D’ + 2) % 7 = (D’ + 2) % 7
即把式子中是7的倍数去除再求7的余数，结果不变。

把公式1写成
D=year×(7×52+1)+[year/4]-[year/100]+[year/400]-[year/3200]+[year/86400]+(month-3)×(7×4)+[13×(month+1)/5]-(7+3)+day+2

把是7的倍数项去除，余数结果不变：
D=year+[year/4]-[year/100]+[year/400]-[year/3200]+[year/86400]+[13×(month+1)/5]-3+day+2

此时上面的D就不是原来的总天数了。
整理后得：
D=year+[year/4]-[year/100]+[year/400]-[year/3200]+[year/86400]+[13×(month+1)/5]+day-1 （公式2）

继续简化：
令c = [year / 100] ，如1989年，c=19
令y = year % 100，如1989年，y=89
year = 100c+y = (7×14+2)c+y = 7×14c+2c+y
year ≡ 2c+y (mod 7）

公式2简化为
D=2c+y+[(100c+y)/4]-[(100c+y)/100]+[(100c+y)/400]-[(100c+y)/3200]+[(100c+y)/86400]+[13×(month+1)/5]+day-1
=2c+y+[(25c+y/4]-[c+y/100]+[(c/4+y/400]-[c/32+y/3200]+[c/864+y/86400]+[13×(month+1)/5]+day-1

因为c>0，y>0，所以
D=2c+y+[25c]+[y/4]-[c]-[y/100]+[c/4]+[y/400]-[c/32]-[y/3200]+[c/864]+[y/86400]+[13×(month+1)/5]+day-4

因为 0<y<=99，所以
[y/100]=0
[y/400]=0
[y/3200]=0
[y/86400]=0

因为c是正整数，所以
[25c]=25c
[c]=c

D=2c+y+25c+[y/4]-c-0+[c/4]+0-[c/32]-0+[c/864]+0+[13×(month+1)/5]+day-1
=26c+y+[y/4]+[c/4]-[c/32]+[c/864]+[13×(month+1)/5]+day-1
=(28-2)c+y+[y/4]+[c/4]-[c/32]+[c/864]+[13×(month+1)/5]+day-1
=y-2c+[y/4]+[c/4]-[c/32]+[c/864]+[13×(month+1)/5]+day-1

w = D % 7 = (y-2c+[y/4]+[c/4]-[c/32]+[c/864]+[13×(month+1)/5]+day-1) % 7

w = (y-2c+[y/4]+[c/4]-[c/32]+[c/864]+[13(m+1)/5]+d-1) % 7 （公式3）

公式3就是著名的蔡勒公式，公式3只适用于计算1582年10月15日之后的星期。其中：
c：世纪数 - 1的值，如 21世纪，则 c = 20。可以理解为年份数字十位之前的数，如2019年，c = 20。
y：年份，取年份的后两位，如2019年，y = 19。如果是1月份和2月份，则看作上一年，即y=18。
m：月份，如果是1月和2月，则看作上一年的13月和14月。
d：日数，如2019年12月8日，d=8。

year年month月day日计算顺序：
if(month <= 2)
{
year–;
m=month+2;
}
y = year % 100;
c = [year / 100];
d = day;

4.2 公元1年1月1日到1582年10月4日计算：
蔡勒有另外的公式：
w = (y-c+[y/4]+[13(m+1)/5]+d+4) % 7 （公式4）

4.3 公元前计算：
我不知道蔡勒有没有计算公元前的公式，但根据上面推算原理，我也推算出了公元前的计算公式：
w = (y-c-[(2-y)/4]+[13(m+1)/5]+d-2) % 7 （公式5）

推算过程：
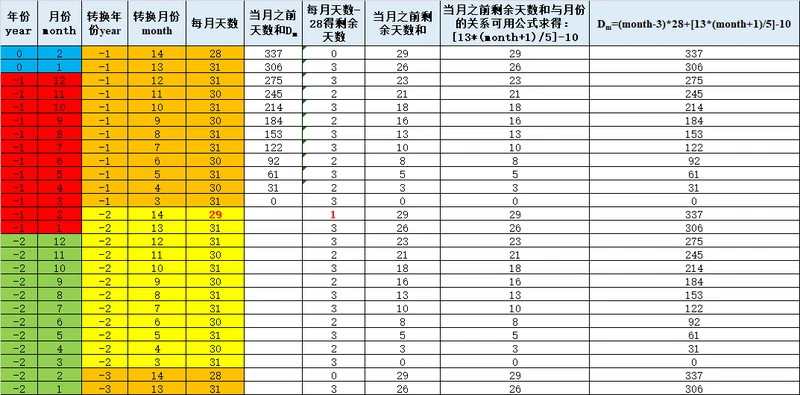
在这里插入图片描述
以0年3月1日为基准，0年3月1日为星期二（序号2）。
计算某日期与基准的天数原理是：（下面所讲的年份月份是转换后的年份月份）
总天数D=-1年到某日期的年的年数总天数×365 + 闰年的次数 - 某日期在当年本月之前月的总天数D_m - 某日期在本月的天数D_d + 1。 (注：这里要+1，与公元后不同）
D=-year×365 + L - D_m - D_d +1

year：年份，公元前年份取负数，如-1年。如果是1月、2月，则year为上一年，year=year-1。
L：闰年次数，L = [-(year-2)/4]
D_m：某日期在本月之前月的总天数，
D_m = (month-3)×28+[13×(month+1)/5]-10
month：月份，当month <= 2时，month = month +2
D_d：某日期在本月的天数，D_d = day

D = -year×365 + [-(year-2)/4] - (month-3)×28 - [13×(month+1)/5] + 10 - day + 1
w = 2 - D % 7 = (2 - D) % 7

(2 - D) 简化后的结果：
2 - D ≡ (y-c-[(2-y)/4]+[13(m+1)/5]+d-2) (mod 7）
所以：
w = (y-c-[(2-y)/4]+[13(m+1)/5]+d-2) % 7

公式3~5的计算过程和顺序相同。当w为负数时，需要加7使其变化正数。
if(w < 0)
w += 7;

4.4 计算代码：

/*计算某日是星期几：*/
int Week(int year, int month, int day)
{
    int y1 = year;
    int m = month;
    int d = day;

    if (month <= 2) //对小于3的月份按上一年的第13、14个月计算
    {
        y1--;
        m = month +12;
    }

    int y = y1 % 100;
    int c = y1 / 100;
    int w;

    if(year < 0) //公元前使用儒略历
        w = (y - c - (2 - y) / 4 + 13 * (m + 1) / 5 + d -2) % 7;  //公元前公式。注意：没有0年。公元前用负数表示，从-1开始。

    else if( ((year > 0 ) && (year < 1582)) || ((year == 1582) && (month < 10)) || ((year == 1582) && (month == 10) && (day < 5)) )  //1582年10月4日之前使用儒略历
        w = (y - c + y / 4 + 13 * (m + 1) / 5 + d + 4) % 7;  //公元1年1月1日至1582年10月4日公式

    else if( (year > 1582) || ((year == 1582) && (month > 10)) || ((year == 1582) && (month == 10) && (day >= 15)) )   //1582年10月15日后使用格里历
        w = (y - 2 * c + y / 4 + c / 4 -c/32 + c/864 + 13 * (m + 1) / 5 + d - 1) % 7;

    else  //没有0年，1582-10-5至1582-10-14之间的日期
        w = 8; //输入的日期不存在则反回8作为标记。请输入非0年或1582-10-5至1582-10-14之外的日期。

    if (w < 0) //如果小于0，则要修正
        w += 7;

    return w;
}

5 打印一个月的日历:

/*打印每月日历*/
void PrintMonthCalendar(int year, int month, int order)
{
    string weekDay[7] = {"日","一","二","三","四","五","六"};
    int days = GetDaysOfMonth(year, month); //获得这个月的天数
    int firstDayWeek = Week(year, month, 1);

    if(firstDayWeek == 8)
    {
        cout << "你输入的日期不存在。请输入非0年或1582-10-5至1582-10-14之外的日期。" << endl;
        exit(0);
    }

    cout << '\n' << endl;
    cout << year << "年" << month << "月" << endl;

    /*打印表头:*/
    int i = 0;
    int k;
    while(i <= 6)
    {
        k = (i + order) % 7;  //按某星期为每周的第一天排序
        cout << weekDay[k] << '\t';
        i++;
    }

    cout << '\n' << endl;

    /*插入1日前的空格（制表符）:*/
    int blankNum;  //1日前的空格（制表符）数量
    blankNum = (firstDayWeek - order) % 7;
    blankNum = blankNum < 0 ? blankNum + 7 : blankNum; //如果是负数，还得加7变成正数
    InsertTab(blankNum);  //插入制表符

    i = 1;
    while(i <= days)
    {
        cout << i << '\t';  //接着从前面打印过的制表符后面开始打印日期
        blankNum ++;  //用blankNum继续计录日期所在的列数

        if((blankNum % 7) == 0) //到第7列结束，切换到下一行输出
            cout << '\n' << endl;

        if((year == 1582) && (month == 10) && (i>=4) && (i<=14)) // 1582年10月5日与1582年10月14日的日期不存，需求跳过
            i=14;

        i++;
    }

    cout << '\n' << endl;
}


/*根据每个月第一天的星期序号插入合适的制表符*/
void InsertTab(int number)
{
    while(number >0 )
    {
        cout << '\t' ;
        number--;
    }
}

参数order是表示每周的第一天为星期的序号。
打印原理是：先打表头，然后计算这个月的1日是星期几，把1日对好表头打印，后续的日期按顺序按位置打印就行。无需计算每日的星期。

打印效果：
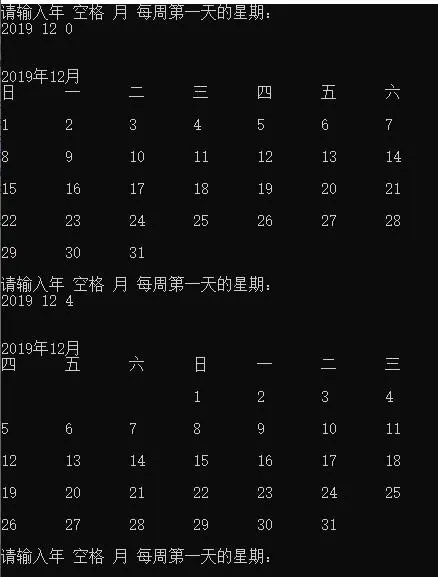
在这里插入图片描述
以上的算法理论上可以计算所有的日期。

感谢吹泡泡的小猫博主的知识。