波函数坍塌

“波函数坍塌”是个量子力学中的概念。不过现在讲的这个算法并不是真正的在算量子力学，他只是借鉴了这样一种概念：
一个东西在“观测”之前拥有无数种状态，而“观测”之后便会固定成为一种状态。而它可能出现的状态越多，就代表其熵越高。而熵越低那他就越容易被“观测”。

当然，我并不学量子力学，上面的概念是算法的思路所体现的。不过就算不理解量子力学，我也能明白算法与实际的量子力学一个最大的出入：状态，在自然界肯定是“连续”的，而在这个算法中状态实际对应一种位图“图案”，是离散的，有一个确定的数目。

不深究“波函数坍塌”在量子力学中的真正含义，只是从眼前这个算法来看，这个名为“波函数坍缩”的算法确实有实用价值，尤其是我关心的——游戏方面。它目前已经用在了一些游戏中，比如《bad north》。
还有《Townscaper》：

GDC上有一篇针对于这个算法的文章：《 Math for Game Developers: Tile-Based Map Generation using Wave Function Collapse in ‘Caves of Qud’》
其中指出，这套算法是 Maxim Gumin 在2016年开发并开源的算法（MIT许可）。
下面，我想先对GitHub上的ReadMe的部分内容翻译一下，然后耐心看一下他的代码。

ReadMe

先从效果上看，这个算法可以生成与输入位图具有局部相似性的结果：


这里 “局部相似性” 的具体含义是：

• 对于结果中任意一个N乘N尺寸的图案，都能在输入中找到。
• N乘N尺寸图案在输入中的分布概率，应该和结果中的N乘N尺寸图案的分布概率是相近的，尽管后者图案的总数更多。换句话说：在“结果”中遇到某一个特定图案的概率，应该趋近于在“输入”中遇到这个图案的概率。

在下面这个例子中，N=3：

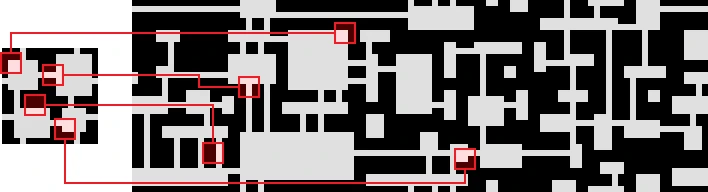
“波函数坍塌” 以一个完全“未观测”的状态来初始化要输出的位图，即每个像素值都是输入位图中颜色的叠加（所以如果输入图是黑与白，那么“未观测状态”将表示为不同程度上的“灰”）。计算中的数值都是“实数”而不是“复数”，所以它实际上并不是量子力学，但这个算法的灵感来自于量子力学。
初始化之后，程序将进入“观测——传播”循环：

• 在每一个“观测”步骤里：从所有未被观测的区域中选择一块拥有最低熵的“N乘N尺寸区域”，随后这个区域就会“坍缩”为一个具体的状态。
• 在每一个“传播”步骤里：新的信息由上一步得到，随后在结果中“传播”。

整体的熵经过每一步都会减小。到最后，就得到了一个完全“已被观测”的状态，也就是说：波函数已经坍缩了。

具体算法

算法可以描述成下面的步骤：

1. 读取输入的位图，得到数个“N乘N尺寸图案”。
   (可选：将原始的图案进行旋转和翻转形成新的图案，来扩充图案的数目）
2. 创建一个列表来容纳结果（这个列表可以称为 “波”），其中的每一个元素都代表了一个“N乘N尺寸图案”的 “状态”。这里的 “状态” 将存储为：与“N乘N尺寸图案”一一对应的布尔类型系数，false表示对应的图案是禁用的，true表示对应的图案还未被禁用。
3. 将列表以一个“未被观测”的状态初始化，例如将列表中所有元素的所有布尔值都设为true。
4. 循环：
   观察：从“波”（指结果列表）中找一个元素，它拥有最小且非零的熵。如果没有找到这样的元素（表示所有的元素的熵都是0，或者熵值无法计算），那么就跳出循环进行第5步。如果找到了这样的元素，就将这个元素根据系数与“N乘N尺寸图案”的分布而坍缩”为一个具体的状态。
   传播：将上一步中得到的信息传播。
5. 到此为止，所有的元素都要么进入一个“已被观测”的状态（即只有一个系数是true，其余都是false），要么进入一个“矛盾”状态（即所有的系数都是false）。前者将会顺利返回结果，后者表示失败了。

代码观察

0）资源

在工程的samples目录中存放着位图资源，其中有“单个的位图”或“文件夹”：

而其中的“文件夹”则存放着一些看似关联性很强的位图以及一个data.xml文件：

而工程中的samples.xml则存放着描述：

<samples>
	<overlapping name="Chess" N="2" periodic="True"/>
	<overlapping name="LessRooms" N="3" periodic="True"/>
	<simpletiled name="Summer" width="15" height="15"/>
	<simpletiled name="Castle" width="20" height="20"/>
	... 
</samples>

1）Main.cs

——程序的入口。

开始，从samples.xml得到数据。

XDocument xdoc = XDocument.Load("samples.xml");

然后，对其中名字为"overlapping"或"simpletiled"的节点进行遍历。

 foreach (XElement xelem in xdoc.Root.Elements("overlapping", "simpletiled"))

之后便是针对于每个节点的操作：

1.创建Model

Model类有两个子类：OverlappingModel和SimpleTiledModel，它根据xml节点的名字是"overlapping"还是"simpletiled"来创建对应的Model，同时也从xml节点中得到参数：

if (xelem.Name == "overlapping") model = new OverlappingModel(name, xelem.Get("N", 2), xelem.Get("width", 48), xelem.Get("height", 48),
    xelem.Get("periodicInput", true), xelem.Get("periodic", false), xelem.Get("symmetry", 8), xelem.Get("ground", 0));
else if (xelem.Name == "simpletiled") model = new SimpleTiledModel(name, xelem.Get<string>("subset"),
    xelem.Get("width", 10), xelem.Get("height", 10), xelem.Get("periodic", false), xelem.Get("black", false));
else continue;

2.运行Model

随后，调用Model类的接口Run，如果成功便调用接口Graphics来保存结果，否则就再试一次（最多试10次）

for (int k = 0; k < 10; k++)
{
    int seed = random.Next();
    bool finished = model.Run(seed, xelem.Get("limit", 0));
    if (finished)
    {
        model.Graphics().Save($"{counter} {name} {i}.png");
        break;
    }
    else Console.WriteLine("CONTRADICTION");
}

2）Model.cs

——其中存着Model这个基类的定义。在Main.cs中，构造函数、Run、Graphics这个三个接口被调用，因此下面要着重留意它们。

首先，Model是一个抽象类

abstract class Model

它的构造函数很简单，只是得到尺寸参数，子类的构造函数将复杂得多。

protected Model(int width, int height)
{
    FMX = width;
    FMY = height;
}

而Graphics是个纯虚函数，期望子类实现细节。

public abstract System.Drawing.Bitmap Graphics();

因此重点是Run，它执行的步骤如下：

1. 当wave不是空的时候，调用Init。
2. 调用Clear
3. 在有限的次数内循环：先调用Observe，如果结果非空，则直接返回结果；否则调用Propagate

public bool Run(int seed, int limit)
{
    if (wave == null) Init();

    Clear();
    random = new Random(seed);

    for (int l = 0; l < limit || limit == 0; l++)
    {
        bool? result = Observe();
        if (result != null) return (bool)result;
        Propagate();
    }

    return true;
}

值得一提的是，Run、Init、Observe、Propagate搜没有被子类覆写，也就是说，其中的逻辑在子类中是一样的。至于Clear，它在其中一个子类中被扩充了一些操作，随后细看。
下面仔细看下Init、Observe、Propagate、Clear中的内容。

1. Init()

——对一些变量进行初始化，数组变量也会在此指定它们各自的尺寸。

首先是wave（ 波），他表示了FMX * FMY个元素的T个状态。例如：wave[i][t]表示波中第i个元素的第t个状态有没有被禁用。

wave = new bool[FMX * FMY][];
for (int i = 0; i < wave.Length; i++)
    wave[i] = new bool[T];

其中FMX和FMY由xml节点上的属性指定，表示输出结果的尺寸，缺省都是48。而T表示状态的个数，其值则由子类各自的方式计算。

---

compatible将表示波中一个元素在一个状态上与4个方向上的邻居元素有多少个兼容的状态。例如：compatible[i][t][d]=n表示波中第i个元素在处于第t个状态时，d所对应的方向上会允许邻居有n个状态。

compatible = new int[wave.Length][][];
for (int i = 0; i < wave.Length; i++)
{
    compatible[i] = new int[T][];
    for (int t = 0; t < T; t++) compatible[i][t] = new int[4];
}

其中4是代表左、上、右、下 四个方向。同时代码里提供了一些static数组变量来使相关的算法更方便，如DX[d]表示第d个方向上的X坐标偏移，opposite[d]表示第d个方向对面是第几个方向。

protected static int[] DX = { -1, 0, 1, 0 };
protected static int[] DY = { 0, 1, 0, -1 };
static int[] opposite = { 2, 3, 0, 1 };

---

Model有个成员weights表示T个状态各自的概率，或者叫 “权重”，由子类各自的方式计算。在Init中，一些与它直接关联的变量被计算，包括：

• weightLogWeights：权重乘Log权重。和weights一样也有T个元素，只不过其中每个元素的值都是对应weights中的元素计算得到，公式为$weightLogWeights[t]=weights[t]\times {\log }_{e}weights[t]$
• sumOfWeights：weights中所有元素相加的总和。
• sumOfWeightLogWeights：weightLogWeights中所有元素相加的总和。

weightLogWeights = new double[T];
sumOfWeights = 0;
sumOfWeightLogWeights = 0;
for (int t = 0; t < T; t++)
{
    weightLogWeights[t] = weights[t] * Math.Log(weights[t]);
    sumOfWeights += weights[t];
    sumOfWeightLogWeights += weightLogWeights[t];
}

---

熵在此算法中的公式为：
$${\log }_e权重总和-\frac{权重乘Log权重的总和}{权重总和}$$

因此初始的熵（startingEntropy）为：

startingEntropy = Math.Log(sumOfWeights) - sumOfWeightLogWeights / sumOfWeights;

---

sumsOfOnes表示波中每个元素还有几个状态可用

sumsOfOnes = new int[FMX * FMY];

---

上面的sumOfWeights、sumOfWeightLogWeights都是由所有权重值计算的，然而在运行时，波中的元素由于一些状态被“禁止”了，因此那些状态的权重值需要移除。下面由sumsOfWeights和sumsOfWeightLogWeights来表示波中每个元素在运行时实时的权重层总和、权重乘Log权重的总和。

sumsOfWeights = new double[FMX * FMY];
sumsOfWeightLogWeights = new double[FMX * FMY];

---

波中每个元素在运行时的熵值

entropies = new double[FMX * FMY];

---

stack是一个栈的结构，元素类型为(int,int)。例如：(i,t)对应波中第i个元素的t状态。
唯一的入栈操作是在Ban(int i, int t)函数中，可以认为这个栈中存储了被禁用掉的“元素的状态”。
而唯一的出栈操作是在Propagate()函数中，可以认为传播函数将传播“一个元素的状态被禁掉”这个信息。

stack = new (int, int)[wave.Length * T];
stacksize = 0;

---

此外，Model类还有一个成员，虽然没有出现在Init中，但很重要，是int[][][] propagator。它的内容是在子类的构造函数中完成的，算是子类间最大的区别了。
propagator指明了状态之间兼容（或者说连接）的关系。例如：propagator[d][t1][c] = t2表示t1状态在第d个方向上可以与t2连接，其中c取值0~n，这里的n指的是t1状态在第d个方向上会与多少个状态有这样的连接关系。

2. Clear()

——负责在正式运行之前初始化一些数据，这些数据会在正式运行之时发生变化。

整个Clear函数都在一个循环内，针对于每一个元素进行操作

for (int i = 0; i < wave.Length; i++)

初始，所有状态都是true，表示一切皆有可能，即处于完全未观测的状态。

for (int t = 0; t < T; t++)
    wave[i][t] = true;

compatible的初始值由propagator中的数据得到，不过值得注意的是，这里compatible[i][t][d]指的是i号元素第t个状态的d方向所对面的方向所存在的可兼容（或者说连接）的状态的数目。之所以要存储对面是和之后传播函数中的用法有关，一会儿可以留意。

for (int t = 0; t < T; t++)
    for (int d = 0; d < 4; d++) 
        compatible[i][t][d] = propagator[opposite[d]][t].Length;

每个元素的sumsOfOnes在一开始都是weights的长度（也就是T的值，状态的总数目）。

sumsOfOnes[i] = weights.Length;

每个元素的权重总和、权重乘Log权重的总和、熵也都是在Init中用所有状态的权重计算的结果。

sumsOfWeights[i] = sumOfWeights;
sumsOfWeightLogWeights[i] = sumOfWeightLogWeights;
entropies[i] = startingEntropy;

3. Observe()

——“观察”阶段

局部变量min表示这次观察到所发现最低的 “熵” 。

double min = 1E+3;

局部变量argmin是上面最低的熵所对应的波里元素的索引。

int argmin = -1;

随后，遍历波中所有的元素，来找最低的熵，步骤如下：

1. 先看sumsOfOnes[i]，他表示当前还没有被禁用的状态的数目，记为amount。
   amount是0：表示这个元素不存在任何可用的状态了，这意味着出现了 矛盾，于是观察阶段直接返回false，这也意味着这次运行失败了。
   amount是1：表示这个元素“已被观察”了，因此不需要计算了，跳过此元素。
   amount大于1：表示还有多个可能的状态，要开始计算熵了，那么继续执行。
2. 接下来看entropies[i]，他表示这个元素由公式计算出来的熵，记为entropy
3. 然而，由于我们的状态实际上是 “离散” 的（即有一个具体的数目），所以实际可能会计算出很多相同值的元素，他们都是最小值，如果就这样使用公式计算出来的值作为熵的话，那么“寻求最小值”的这一操作最后会得到它们中的“第一个”或者“最后一个”（取决于比较时用的是<还是<=）。因此给entropy加一个无规律的随机较小的数（称之为噪声）可以使这些原本具有相同值的元素产生细微的差别，这样那些原本具有相同值的元素都有可能成为“最小值”，entropy加上细小噪声之后记为entropy'
4. 使用entropy'与min比较，如果更小则更新min和argmin。

for (int i = 0; i < wave.Length; i++)
{
    int amount = sumsOfOnes[i];
    if (amount == 0) return false;

    double entropy = entropies[i];
    if (amount > 1 && entropy <= min)
    {
        double noise = 1E-6 * random.NextDouble();
        if (entropy + noise < min)
        {
            min = entropy + noise;
            argmin = i;
        }
    }
}

之后，看argmin是否等于初始值-1，如果是，则表明上述遍历的所有元素的状态数目都是1，即整个波被“完全观测”到了。那么就把波中的结果存到observed这个成员中，它会用来在Graphics函数中生成结果位图。

if (argmin == -1)
{
    observed = new int[FMX * FMY];
    for (int i = 0; i < wave.Length; i++) for (int t = 0; t < T; t++) if (wave[i][t]) { observed[i] = t; break; }
    return true;
}

如果走到这里还没有返回，则说明是大多数的情况：既没有进入“矛盾”状态，也没有进入“完全观测”的状态。
那么，就“观测”一下拥有最低“熵”的元素：从所剩可用的状态中带权重地随机出一个。

double[] distribution = new double[T];
for (int t = 0; t < T; t++) distribution[t] = wave[argmin][t] ? weights[t] : 0;
int r = distribution.Random(random.NextDouble());

最后决定的状态记为了r，这样，对于这个元素，除了r之外的所有状态都应该是false。那么遍历这个元素的所有状态，对其中应该是false但却不是false的状态执行Ban操作。

bool[] w = wave[argmin];
for (int t = 0; t < T; t++) if (w[t] != (t == r)) Ban(argmin, t);

返回null，表示还在观测之中。

return null;

4. Ban(int i, int t)

——表示要禁用掉一个元素的一个状态。例如Ban(i,t)表示禁用掉i号元素的t号状态。

首先，顾名思义将wave[i][t]写为false，表示此状态被禁掉。

wave[i][t] = false;

但除此之外还需要更新相关的数据，并做些操作。

将此元素的这个状态 入栈，这个栈随后会在传播函数中进行操作。

stack[stacksize] = (i, t);
stacksize++;

此元素可用的状态数目减一

sumsOfOnes[i] -= 1;

更新权重值相关的数据

sumsOfWeights[i] -= weights[t];
sumsOfWeightLogWeights[i] -= weightLogWeights[t];

最后用公式更新此元素的熵值

double sum = sumsOfWeights[i];
entropies[i] = Math.Log(sum) - sumsOfWeightLogWeights[i] / sum;

5. Propagate()

——传播栈里“一个元素的一个状态被禁掉”这一信息

它要针对于当前栈内所有的元素做操作，因此整个函数都是在一个循环中的

while (stacksize > 0)

首先，拿到这个元素，记为e1。

var e1 = stack[stacksize - 1];
stacksize--;

栈中元素的第一个int数据就是波中元素的索引号，记为i1

int i1 = e1.Item1;

那么这个元素的位置也可以计算得到

int x1 = i1 % FMX, y1 = i1 / FMX;

下面的所有操作都是针对于四个方向进行

for (int d = 0; d < 4; d++)

d方向上的邻居的位置，也可以计算得到

int dx = DX[d], dy = DY[d];
int x2 = x1 + dx, y2 = y1 + dy;

通过邻居的位置，可以算出邻居元素的索引号，记为i2

int i2 = x2 + y2 * FMX;

之后，便是传播函数中真正要做的核心任务：判断波中邻居元素的一个状态是否要禁掉。这主要是通过compatible来判断的：
由于compatible[i][t][d]存储了波中第i个元素的t状态在d方向上有几个状态可以与其兼容。如果其值为0，则表示这个元素的t状态在d方向上已经没有与之兼容的状态了，那么不管d是几，i元素的t状态都需要被禁掉。
此部分的代码如下：

int[] p = propagator[d][e1.Item2];
for (int l = 0; l < p.Length; l++)
{
    int t2 = p[l];
    compatible[i2][t2][d]--;
    if (compatible[i2][t2][d] == 0) Ban(i2, t2);
}

此部分较为抽象，因此假定d=0来理解一下这段代码：
e1.Item2是要传播的这个元素的状态，记为t1。
propagator[d][t1]值的类型是int[]，存放着t1状态在左方向上所有与之兼容的状态，下面就遍历这些状态：

• 记兼容的状态为t2。（说明t1状态在左方向上与t2兼容）。
• 由于i2是要传播的元素i1在左方向上的邻居，compatible[i2][t2][d]的值就是i2的t2状态在右方向上有多少状态与之兼容。（注意是右而不是左，因为在Clear()函数中存的都是d方向上对面的方向上的数据）
• compatible[i2][t2][d]需要减一，因为它左边的i1的t1状态已经被禁掉了
• 看看compatible[i2][t2][d]是不是已经减为0了，如果是的话，i2的t2状态就要被禁掉了。

3）OverlappingModel.cs

OverlappingModel是Model类的子类，主要是在propagator的生成上有很大的特化。它的“图案”来源是从“输入位图”中提取的更小尺寸的单元。而对于状态之间是否兼容，它是看“图案”是否有重叠的部分，这大概也是其名字Overlapping的来源。

这些操作是放在其构造函数中的。构造函数有多个参数，可以在Main.cs中看到：这些参数都是从xml节点中得到的（如果没有则是缺省值）

public OverlappingModel(string name, int N, int width, int height, bool periodicInput, bool periodicOutput, int symmetry, int ground)
        : base(width, height)

N是OverlappingModel这个子类的成员，表示最开始讨论时一个“图案”的尺寸。由xml节点中属性指定，默认是3。

this.N = N;

---

通过name找到“输入位图”，记为bitmap，而它的尺寸记为SMX和SMY

var bitmap = new Bitmap($"samples/{name}.png");
int SMX = bitmap.Width, SMY = bitmap.Height;

接下来，统计所有出现的颜色，放到colors列表中。而sample则存储了“输入位图”对应像素的颜色的“索引号”。之后关于像素颜色的数据都是由“颜色索引号”表示的。

byte[,] sample = new byte[SMX, SMY];
colors = new List<Color>();

for (int y = 0; y < SMY; y++) 
	for (int x = 0; x < SMX; x++)
	{
	    Color color = bitmap.GetPixel(x, y);
	
	    int i = 0;
	    foreach (var c in colors)
	    {
	        if (c == color) break;
	        i++;
	    }
	
	    if (i == colors.Count) colors.Add(color);
	    sample[x, y] = (byte)i;
	}

此处需要讨论的是：“颜色索引号”是byte类型的，是8位，也就是说只能表示256种颜色。那么这里一个隐含的条件就是——“输入位图”中出现的颜色数目不能超过256。不过，考虑到“输入位图”的尺寸都比较小，大概16*16左右，在最极端的情况下，16*16中出现的颜色也不会超过256。此外，考虑到为了让“图案”能更自然拼接，“输入位图”中的颜色不能太过分散，否则会使一个状态所能兼容的邻居的状态太少，甚至为零。综上，256这个颜色的数目以目前的资源看来是比较宽裕的。

---

接下来，声明一个局部函数pattern，它之后会嵌入其他的局部函数。

byte[] pattern(Func<int, int, byte> f)
{
    byte[] result = new byte[N * N];
    for (int y = 0; y < N; y++) for (int x = 0; x < N; x++) result[x + y * N] = f(x, y);
    return result;
};

pattern的参数是一个(int,int)=>byte类型的函数。pattern将用参数中的函数来返回一个N乘N尺寸的位图。

---

patternFromSample表示直接从“输入位图”中得到一个“图案”

byte[] patternFromSample(int x, int y) => pattern((dx, dy) => sample[(x + dx) % SMX, (y + dy) % SMY]);

需要注意的是，这里采样时用了取余操作，这意味着超过边界的位置将被“传送”到另一侧，也就是说将“输入位图”看成了“左与右连接”、“上与下连接”的状态。

---

rotate表示对输入的图案旋转90°

byte[] rotate(byte[] p) => pattern((x, y) => p[N - 1 - y + x * N]);

---

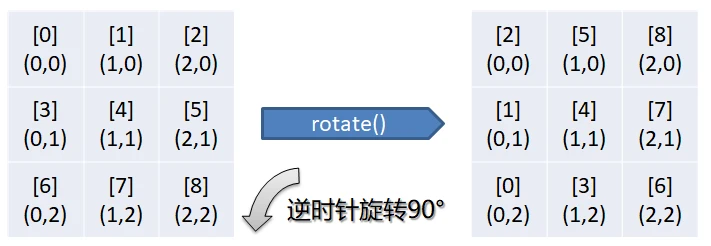
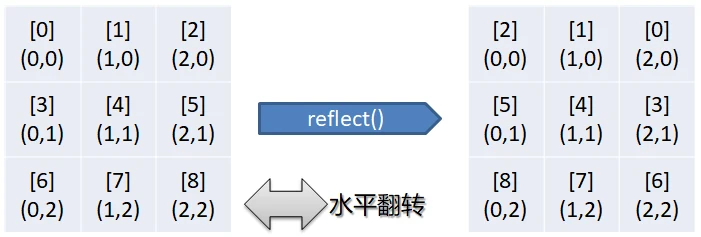
reflect表示对输入的图案

byte[] reflect(byte[] p) => pattern((x, y) => p[N - 1 - x + y * N]);

---

接下来，想要实现一种“图案”与“索引号”之间的转换，“索引号”的类型是long，接下来有关“图案”的操作也都以“图案索引号”来表示。我想这么做的目的应该是能快速比较两个“图案”是否相同，类似于“哈希”。

不过在此之前，为了便于计算先记两个局部变量：
C为颜色的数目。而W是C的N*N次方。

int C = colors.Count;
long W = C.ToPower(N * N);

“图案”转换为“索引号”的公式。“索引号”相当于一个C进制的数字，位数是位图中的像素数。

long index(byte[] p)
{
    long result = 0, power = 1;
    for (int i = 0; i < p.Length; i++)
    {
        result += p[p.Length - 1 - i] * power;
        power *= C;
    }
    return result;
};

“图案索引号”转回“图案”的过程就是上面的逆运算：

byte[] patternFromIndex(long ind)
{
    long residue = ind, power = W;
    byte[] result = new byte[N * N];

    for (int i = 0; i < result.Length; i++)
    {
        power /= C;
        int count = 0;

        while (residue >= power)
        {
            residue -= power;
            count++;
        }

        result[i] = (byte)count;
    }

    return result;
};

值得讨论的是，“图案索引号”的类型是long，64位，也就是说最多能存储2^64种图案。这里需要思考它有没有超界的情况。考虑一下，输入位图如果尺寸是16*16，那么颜色的种类在极端情况下有256个，而一个“图案”是3*3尺寸的话，“图案”最极端情况下有256^(3*3)个，其实超过了2^64一点（2^64=256^8）。但是正如之前讨论的，输入位图中的颜色数目应该是远小于256。因此2^64可以说是很充足了。

---

下面，开始统计“图案”的信息了。

weights将记录每种图案出现的个数。（注意这是局部变量，基类有一个同名的成员）

Dictionary<long, int> weights = new Dictionary<long, int>();

ordering将有序地存储“图案索引号”

List<long> ordering = new List<long>();

随后就是得到”图案“数据了，需要注意的是：

• “图案”并不是由输入位图“分割”的，换句话说，“图案”是有重叠的。例如，在“图案”是3乘3，“输入位图”是9*9的情况下，“图案”数目应该有7*7个。当然，如果将输入的位图看作是“左右连续且上下连续”的，那么“图案”数目就是9*9个了，是否这么做取决于periodicInput参数。
• “图案”可以经过旋转或反转形成新的“图案”来扩充数目，具体多少个这样的新图案由symmetry参数指定

for (int y = 0; y < (periodicInput ? SMY : SMY - N + 1); y++) 
    for (int x = 0; x < (periodicInput ? SMX : SMX - N + 1); x++)
    {
        byte[][] ps = new byte[8][];

        ps[0] = patternFromSample(x, y);
        ps[1] = reflect(ps[0]);
        ps[2] = rotate(ps[0]);
        ps[3] = reflect(ps[2]);
        ps[4] = rotate(ps[2]);
        ps[5] = reflect(ps[4]);
        ps[6] = rotate(ps[4]);
        ps[7] = reflect(ps[6]);

        for (int k = 0; k < symmetry; k++)
        {
            long ind = index(ps[k]);
            if (weights.ContainsKey(ind)) weights[ind]++;
            else
            {
                weights.Add(ind, 1);
                ordering.Add(ind);
            }
        }
    }

可以看到，原始的“图案”经过“旋转”或”翻转“形成了7个新的图案：

序号	图案
1	原图水平翻转
2	原图逆时针旋转90°
3	[2]图水平翻转
4	原图逆时针旋转180°
5	[4]图水平翻转
6	原图逆时针旋转270°
7	[6]图水平翻转

这几个图案都计算出了“索引号”，随后添加到weights和ordering中或是增加weights中对应的数目。

基类成员状态数目T就是图案的个数

T = weights.Count;

子类成员patterns将记录图案的“颜色索引号”数组

patterns = new byte[T][];

随后，patterns和基类的weights都由刚才统计出的数据得到

base.weights = new double[T];

int counter = 0;
foreach (long w in ordering)
{
    patterns[counter] = patternFromIndex(w);
    base.weights[counter] = weights[w];
    counter++;
}

---

最后，计算propagator这个在传播函数中扮演核心地位的数据，

首先，创建一个局部函数agrees用来计算两个图案在基于一个“偏移”的部分上是否有重叠

bool agrees(byte[] p1, byte[] p2, int dx, int dy)
{
    int xmin = dx < 0 ? 0 : dx, xmax = dx < 0 ? dx + N : N, ymin = dy < 0 ? 0 : dy, ymax = dy < 0 ? dy + N : N;
    for (int y = ymin; y < ymax; y++) for (int x = xmin; x < xmax; x++) if (p1[x + N * y] != p2[x - dx + N * (y - dy)]) return false;
    return true;
};

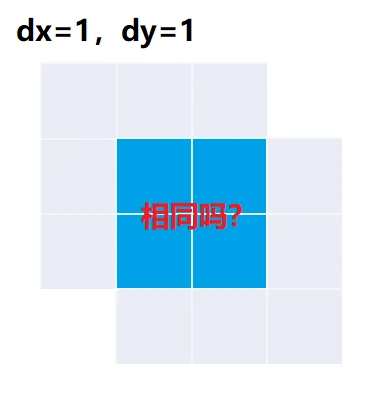
随后，使用这个函数来计算状态之间的兼容关系：

propagator = new int[4][][];
for (int d = 0; d < 4; d++)
{
    propagator[d] = new int[T][];
    for (int t = 0; t < T; t++)
    {
        List<int> list = new List<int>();
        for (int t2 = 0; t2 < T; t2++)
            if (agrees(patterns[t], patterns[t2], DX[d], DY[d]))
                list.Add(t2);
        propagator[d][t] = new int[list.Count];
        for (int c = 0; c < list.Count; c++)
            propagator[d][t][c] = list[c];
    }
}

4）SimpleTiledModel.cs

SimpleTiledModel是Model的一个子类。和OverlappingModel不同的是：OverlappingModel从一个单一的“输入位图”中得到数个“图案”，而SimpleTiledModel的图案是预先已经知道了，且他们之间的“兼容”关系也已在data.xml文件中写好：

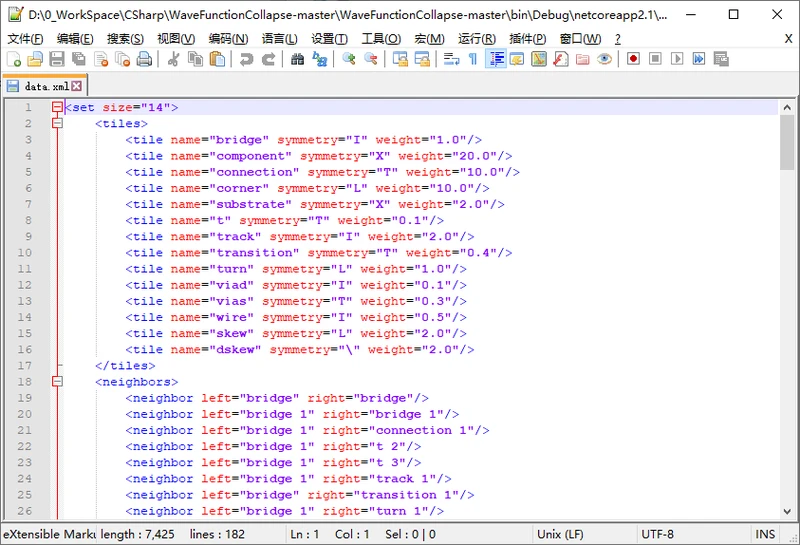
对输入数据的处理以及propagator的设计，和上一个子类一样也是在它的构造函数中的，下面对其研究：

tile是一个局部函数，和上一个子类的pattern职责类似。

Color[] tile(Func<int, int, Color> f)
{
    Color[] result = new Color[tilesize * tilesize];
    for (int y = 0; y < tilesize; y++) for (int x = 0; x < tilesize; x++) result[x + y * tilesize] = f(x, y);
    return result;
};

tile函数被rotate使用，效果是使输入的图像逆时针旋转90°。

Color[] rotate(Color[] array) => tile((x, y) => array[tilesize - 1 - y + x * tilesize]);

tiles将要存储所有的“图案”，而tilenames则存储对应的名字。

tiles = new List<Color[]>();
tilenames = new List<string>();

tempStationary是个变长数组，数据最终将进入weights中。

var tempStationary = new List<double>();

firstOccurrence记录了一个 “原图案” 第一次出现的位置。这里是“原图案”而不是“图案”，是因为“图案本身”有可能变种成为新的“图案”。随后创建“图案”的代码可以看到更多细节。

Dictionary<string, int> firstOccurrence = new Dictionary<string, int>();

下面的action列表就比较抽象了，它指的是一个图案经过一个 “操作” 将会变成哪一个图案。例如：action[i][a] = j表示第i个图案经过a号操作将会变成第j个图案。这一信息将会在之后制作propagator的时候使用，因此在随后创建“图案”时要得到这一信息。此外，action的数目也就是状态的数目T。

List<int[]> action = new List<int[]>();

关于 “操作” ，总共有8个，在最后综合代码的表现后可以明白其意义：

序号	操作
0	原图
1	原图逆时针旋转90°
2	原图逆时针旋转180°
3	原图逆时针旋转270°
4	原图水平翻转
5	原图逆时针旋转90°再水平翻转
6	原图逆时针旋转180°再水平翻转
7	原图逆时针旋转270°再水平翻转

下面，就进入创建图案的步骤。

从xml文件中得到图案的信息

这一部分都在一个循环中，它在遍历xml节点

foreach (XElement xtile in xroot.Element("tiles").Elements("tile"))

“原图案”的名字在xml节点的属性中

string tilename = xtile.Get<string>("name");

随后，T被临时的赋值。由于action的数目在执行完这次循环后会变，但是需要记录一个执行前的数目，于是就临时给了T。（当然，T的值在所有都执行完之后还是会被赋值为action最后的数目）

T = action.Count;

“原图案”第一次出现的位置

firstOccurrence.Add(tilename, T);

sym表示对称模式，在xml文件中指定。

char sym = xtile.Get("symmetry", 'X');

cardinality是包含“变种图案”的数目。例如2就表示原图案+原图案逆时针旋转90°。例如4就表示原图案+原图案逆时针旋转90°+原图案逆时针旋转180°+原图案逆时针旋转270°。至于其值具体是多少，是根据sym的值决定的。

int cardinality;

而a和b是两个局部函数。a用来表示“逆时针旋转90°”，b用来表示“水平翻转”。这样，通过组合a和b就能获得8个 “操作”。至于具体的内容，也是根据sym的值决定的。

Func<int, int> a, b;

cardinality、a、b 都是由具体的对称模式决定的，但因为数据比较抽象，因此直接列出对应的结果更容易理解。现在，先看得到他们之后的逻辑。

然后，就是将每一个“变种图案”及其对应“操作”的映射存入action。值得一提的是：使用a和b局部函数所计算得到的结果是相对于“原图案”的偏移值，因此最后的结果需要加上“原图案”的位置（现在是T的值）。

for (int t = 0; t < cardinality; t++)
{
    int[] map = new int[8];

    map[0] = t;
    map[1] = a(t);
    map[2] = a(a(t));
    map[3] = a(a(a(t)));
    map[4] = b(t);
    map[5] = b(a(t));
    map[6] = b(a(a(t)));
    map[7] = b(a(a(a(t))));

    for (int s = 0; s < 8; s++)
        map[s] += T;

    action.Add(map);
}

然后，读取位图文件，并旋转得到变种的位图数据

Bitmap bitmap = new Bitmap($"samples/{name}/{tilename}.png");
tiles.Add(tile((x, y) => bitmap.GetPixel(x, y)));
tilenames.Add($"{tilename} 0");

for (int t = 1; t < cardinality; t++)
{
    tiles.Add(rotate(tiles[T + t - 1]));
    tilenames.Add($"{tilename} {t}");
}

tempStationary将记录权重值，默认这个图案的权重值是1.0，不过xml中也可以指定其他的值。

for (int t = 0; t < cardinality; t++)
	tempStationary.Add(xtile.Get("weight", 1.0f));

至此，所有“图案”信息便都被加入了。

下面，看下刚才没讨论的各种对称模式所对应的变种数目cardinality以及各种 “操作” 所映射的“图案”是第几个（“第几个”指相对于“原图案”的偏移）。

---

X：
就像字母X的形状一样，在四个方向上都对称，这意味着如何旋转和翻转都不会产生新的图案。例子是：

cardinality = 1;
a = i => i;
b = i => i;

cardinality:	0
map[0] = t	0
map[1] = a(t)	0
map[2] = a(a(t))	0
map[3] = a(a(a(t)))	0
map[4] = b(t)	0
map[5] = b(a(t))	0
map[6] = b(a(a(t)))	0
map[7] = b(a(a(a(t))))	0

\：
就像斜杠一样，在斜45°方向，以及与之垂直的方向上都是对称的。例子如：

通过旋转90°可以得到变种：

cardinality = 2;
a = i => 1 - i;
b = i => 1 - i;

cardinality:	0	1
map[t][0] = t	0	1
map[t][1] = a(t)	1	0
map[t][2] = a(a(t))	0	1
map[t][3] = a(a(a(t)))	1	0
map[t][4] = b(t)	1	0
map[t][5] = b(a(t))	0	1
map[t][6] = b(a(a(t)))	1	0
map[t][7] = b(a(a(a(t))))	0	1

I：
就像字母I的形状一样，在竖直与水平方向上都是对称的。例如：

通过旋转90°可以得到变种：

cardinality = 2;
a = i => 1 - i;
b = i => i;

cardinality:	0	1
map[t][0] = t	0	1
map[t][1] = a(t)	1	0
map[t][2] = a(a(t))	0	1
map[t][3] = a(a(a(t)))	1	0
map[t][4] = b(t)	0	1
map[t][5] = b(a(t))	1	0
map[t][6] = b(a(a(t)))	0	1
map[t][7] = b(a(a(a(t))))	1	0

T：
就像字母T一样，只在竖直方向上对称。例如：

通过旋转，可以得到3个变种：

cardinality = 4;
a = i => (i + 1) % 4;
b = i => i % 2 == 0 ? i : 4 - i;

cardinality:	0	1	2	3
map[t][0] = t	0	1	2	3
map[t][1] = a(t)	1	2	3	0
map[t][2] = a(a(t))	2	3	0	1
map[t][3] = a(a(a(t)))	3	0	1	2
map[t][4] = b(t)	0	3	2	1
map[t][5] = b(a(t))	3	2	1	0
map[t][6] = b(a(a(t)))	2	1	0	3
map[t][7] = b(a(a(a(t))))	1	0	3	2

L：
就像字母L一样，仅在斜45°方向上对称。例如：

通过旋转可以得到3个变种：

cardinality = 4;
a = i => (i + 1) % 4;
b = i => i % 2 == 0 ? i + 1 : i - 1;

cardinality:	0	1	2	3
map[t][0] = t	0	1	2	3
map[t][1] = a(t)	1	2	3	0
map[t][2] = a(a(t))	2	3	0	1
map[t][3] = a(a(a(t)))	3	0	1	2
map[t][4] = b(t)	1	0	3	2
map[t][5] = b(a(t))	0	3	2	1
map[t][6] = b(a(a(t)))	3	2	1	0
map[t][7] = b(a(a(a(t))))	2	1	0	3

制作propagator

除了propagator外，再创建一个临时的tempPropagator同样也来存储状态之间的兼容情况。所不同的是：tempPropagator的类型是bool[][][]，它存储了所有状态之间的兼容情况是true还是false，例如：tempPropagator[d][t1][t2] = true表示t1状态在d方向上可以与t2兼容。由于它存储了所有状态两两之间的兼容情况，而实际上很多状态在一个方向上能兼容的状态数目是较少的，所以可想而知其中很多元素都是false，这意味着浪费了很多空间，导致它会比propagator占用更大的空间。因此算法的思路是用tempPropagator做计算，信息最后还是会转换到propagator中。

propagator = new int[4][][];
var tempPropagator = new bool[4][][];
for (int d = 0; d < 4; d++)
{
    tempPropagator[d] = new bool[T][];
    propagator[d] = new int[T][];
    for (int t = 0; t < T; t++) tempPropagator[d][t] = new bool[T];
}

---

接下来是一个循环，遍历了所有名为“neighbor”的xml节点。

foreach (XElement xneighbor in xroot.Element("neighbors").Elements("neighbor"))

其中每一个xml节点都存了两个“图案”：左边的、和右边的，代表左边的图案放在左边可以兼容右边的图案放右边。
首先从xml节点上读取left属性和right属性：

string[] left = xneighbor.Get<string>("left").Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);
string[] right = xneighbor.Get<string>("right").Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);

需要注意的是，left/right属性上的字符串是 “原图案”+变种编号 的形式。用Split分开后，left[0]就是指“原图案”，而left[1]就是变种编号，缺省是0。

接下来，代码上就变得比较抽象了：

首先要求得“左边的图案”的索引号，记为L，那么计算的步骤就是：

1. [left[0]]指“原图案”字符串
2. firstOccurrence[left[0]]指“原图案”第一次出现的位置。
3. action[firstOccurrence[left[0]]]指这个“原图案”所对应的操作映射表。
4. left.Length == 1 ? 0 : int.Parse(left[1])是变种的编号，缺省是0。
5. 因此action[firstOccurrence[left[0]]][left.Length == 1 ? 0 : int.Parse(left[1])]就是“左边的图案”的索引号。

int L = action[firstOccurrence[left[0]]][left.Length == 1 ? 0 : int.Parse(left[1])];

然后，自然

tempPropagator[0][R][L] = true;

但比较麻烦的是，“变种”图案和“原图案”存在着关系。这个意思是：假设“左边的图案”放左边和“右边的图案”放右边可以兼容，那么必定存在——“左边的图案”在旋转180°然后水平翻转之后，放在左边，也和“右边的图案”旋转180°然后水平翻转之后，放右边，可以兼容。即：

tempPropagator[0][action[R][6]][action[L][6]] = true;

类似的假设还有：

tempPropagator[0][action[L][4]][action[R][4]] = true;
tempPropagator[0][action[L][2]][action[R][2]] = true;

然而这只是在d=0即左方向上的兼容关系，只要旋转图像90°，就可以得到一组新的兼容关系。

int D = action[L][1];
int U = action[R][1];
tempPropagator[1][U][D] = true;
tempPropagator[1][action[D][6]][action[U][6]] = true;
tempPropagator[1][action[U][4]][action[D][4]] = true;
tempPropagator[1][action[D][2]][action[U][2]] = true;

---

跳出了这个循环，但是tempPropagator还有操作需要处理：兼容关系存在着一种“对称”：即如果t1在左边和t2在右边兼容，那么t2在右边也一定和t1在左边兼容。这听起来是一句废话，但是由于tempPropagator存储了 状态两两之间的关系，因此这种关系实际上重复存放了两次。

for (int t2 = 0; t2 < T; t2++)
    for (int t1 = 0; t1 < T; t1++)
    {
        tempPropagator[2][t2][t1] = tempPropagator[0][t1][t2];
        tempPropagator[3][t2][t1] = tempPropagator[1][t1][t2];
    }

接下来就比较容易理解了。
首先创建一个稀疏表示Propagator的结构：

List<int>[][] sparsePropagator = new List<int>[4][];
for (int d = 0; d < 4; d++)
{
    sparsePropagator[d] = new List<int>[T];
    for (int t = 0; t < T; t++) sparsePropagator[d][t] = new List<int>();
}

然后对tempPropagator进行统计，存放到sparsePropagator，最后转换到propagator中。

for (int d = 0; d < 4; d++)
    for (int t1 = 0; t1 < T; t1++)
    {
        List<int> sp = sparsePropagator[d][t1];
        bool[] tp = tempPropagator[d][t1];

        for (int t2 = 0; t2 < T; t2++) if (tp[t2]) sp.Add(t2);

        int ST = sp.Count;
        propagator[d][t1] = new int[ST];
        for (int st = 0; st < ST; st++) propagator[d][t1][st] = sp[st];
    }

总结与讨论

虽然 “波函数坍塌” 这个概念很深奥，但是在这个——“生成与输入有相似性的位图”的问题里，或者说就这个算法而言，这个深奥的问题其实已经退变成了一种“按照自然的方式拼接给定图片单元”的问题了（尤其是SimpleTiledModel，其实就是拼接图片单元）。
这样看的话，波就是结果位图，而状态用来表示一个位图的局部的多个可能性，而传播用来在一个状态确定下来后禁掉邻居的状态（由于某些图片单元做连接会产生视觉上的接缝断层）

---

虽然这么看来它的目的很简单，但是算法上还是比较晦涩难懂，主要是由于：

• 大概是为了效率原因，并没有使用面向对象的思想产生多个“类”，而是用了大量的维度不同的数组。
• 为了代码上的“优雅简洁”，用了一些晦涩难懂的写法（例如SimpleTiledModel中处理对称Tile时的a和b局部函数，很抽象）

未来可以尝试用面向对象的思想重构一下代码（但效率会低）。

---

算法是针对于二维的，但作者指出，对于三维是完全一样的思路。未来可以尝试探索三维的版本。

---

另外有一个很重要的问题没有讨论的是：
“资源”要如何生产？他们应该是有要求的：要拼接的“图片单元”必须有可以连接的部分，否则无法拼接。那么具体按照什么样的流程或者方法来生产呢？这是个重要的问题，待后续研究。