
微课视频
课堂辅导视频
课堂辅导视频(二)
知识点讲解
17.2 勾股定理的逆定理
第1课时 勾股定理的逆定理
1.能利用勾股定理的逆定理判定一个三角形是否为直角三角形;(重点)
2.灵活运用勾股定理及其逆定理解决问题;(难点)
3.理解原命题、逆命题、逆定理的概念及关系.(重点)
一、情境导入
古埃及人曾经用下面的方法画直角:将一根长绳打上等距离的13个结,然后用桩钉成一个三角形(如图),他们认为其中一个角便是直角.
你知道这是什么道理吗?
二、合作探究
探究点一:勾股定理的逆定理
【类型一】判断三角形的形状
如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
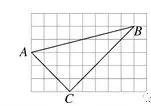
A.直角三角形 B.锐角三角形
C.钝角三角形 D.以上答案都不对

方法总结:要判断一个角是不是直角,可构造出三角形,然后求出三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
【类型二】利用勾股定理的逆定理证明垂直关系
如图,已知在正方形ABCD中,AE=EB,AF=AD.求证:CE⊥EF.
解析:根据题设提供的信息,可将需证明垂直关系的两条线段转化到同一直角三角形中,运用勾股定理的逆定理进行证明.
方法总结:利用勾股定理的逆定理可以判断一个三角形是否为直角三角形,所以此定理也是判定垂直关系的一个主要的方法.
【类型三】勾股数
方法总结:勾股数必须满足:①三个数必须是正整数,例如:2.5、6、6.5满足a2+b2=c2,但是它们不是正整数,所以它们不是勾股数;②一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.
【类型四】运用勾股定理的逆定理解决面积问题

方法总结:将求四边形面积的问题可转化为求两个直角三角形面积和的问题,解题时要利用题目信息构造出直角三角形,如角度,三边长度等.
探究点二:互逆命题与互逆定理
写出下列各命题的逆命题,并判断其逆命题是真命题还是假命题.
(1)两直线平行,同旁内角互补;
(2)在同一平面内,垂直于同一条直线的两直线平行;
(3)相等的角是内错角;
(4)有一个角是60°的三角形是等边三角形.
解析:求一个命题的逆命题时,分别找出各命题的题设和结论将其互换即可得原命题的逆命题.
解:(1)同旁内角互补,两直线平行,真命题;
(2)如果两条直线平行,那么这两条直线垂直于同一条直线(在同一平面内),真命题;
(3)内错角相等,假命题;
(4)等边三角形有一个角是60°,真命题.
方法总结:判断一个命题是真命题需要进行逻辑推理,判断一个命题是假命题只需要举出反例即可.
三、板书设计
1.勾股定理的逆定理及勾股数
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
2.互逆命题与互逆定理
在本课时教学过程中,应以师生共同探讨为主.激励学生回答问题,激发学生的求知欲.课堂上师生互动频繁,既保证课堂教学进度,又提高课堂学习效率.学生在探讨过程中也加深了对知识的理解和记忆.







课时练习
勾股定理的逆定理习题
1.请完成以下未完成的勾股数:
(1)8,15,______;(2)10,26,_____.
2.△ABC中,a2+b2=25,a2-b2=7,又c=5,则最大边上的高是______.
3.以下各组数为三边的三角形中,不是直角三角形的是( ).
A.+1,-1,2 B.7,24,25
C.4,7.5,8.5 D.3.5,4.5,5.5
4.一个三角形的三边长分别为15,20,25,那么它的最长边上的高是( ).
A.12.5 B.12 C. D.9
5.已知:如图,∠ABD=∠C=90°,AD=12,AC=BC,∠DAB=30°,求BC的长.
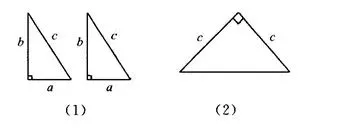
9.如图3中的(1)是用硬纸板做成的形状大小完全相同的直角三角形,两直角边的长分别为a和b,斜边长为c;如图3中(2)是以c为直角边的等腰直角三角形,请你开动脑筋,将它们拼成一个能证明出勾股定理的图形.
(1)画出拼成的这个图形的示意图,写出它是什么图形.
(2)用这个图形推出a2+b2=c2.(勾股定理)
(3)假设图中的(1)中的直角三角形有若干个,你能运用图中的(1)所给的直角三角形拼出另一种能推出a2+b2=c2的图形吗?请画出拼后的示意图.(无需证明)
参考答案
1.17,24 2.略 3.D 4.B 5.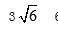
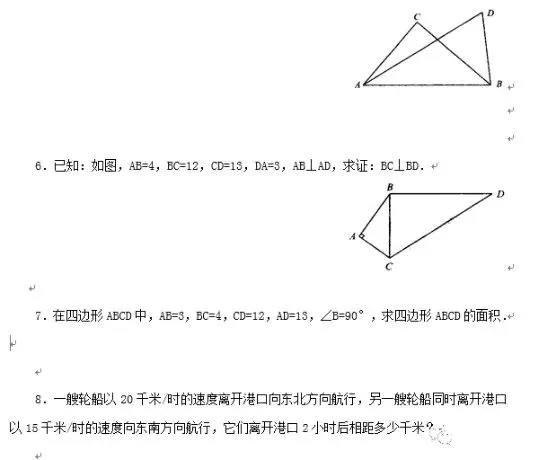
6.提示:∵AB⊥AC,AB=4,DA=3,∴BD=5,又BC=12,CD=13,∴CD2=BC2+BD2,∴∠DBC=90°,∴BC⊥BD 7.36,提示:连结AC得两个直角三角形 8.50千米

▍免责声明:所有素材均来源于网络,仅供学习交流使用,版权归原作者所有,如有侵权请告知,我们会立即删除。

