2024年数据结构串的算法

一：串的概述

串是由零个或多个字符组成的线性表，又称为字符串。串用双引号括起来，但是双引号不属于串的内容。""称为空串，" "称为空格串。例如"ABC"就是一个串，是由A、B、C这三个字符组成的串
定义说串是一种线性表，它其实是一种特殊的线性表，它是由字符组成的

二：串的比较（字符编码概述）

串是通过字符编码进行比较的，计算机中的常用字符使用的是标准的ASCII编码，由7位二进制数表示一个字符，总共128个字符，后来一些特殊字符的出现，128个字符不够用了，于是扩展ASCII编码由8位二进制数表示，总共256个字符。但是世界上有那么多的语言和文字，256个字符显然是不够的，后来就有了Unicode编码，常用的是由16位二进制数表示一个字符，总共可以表示2的16次方个字符，Unicode的前256个字符与ASCII编码完全相同

三：串的顺序存储结构

串与线性表、栈、队列不同，它的操作不在于插入、删除元素，而是各种查找，替换的操作
用一段地址连续的存储单元依次存储串中的字符数据元素

串的顺序存储结构相对来说已经很方便了

四：串的链式存储结构

串的链式存储结构中，一个结点可以存放放个字符(数据)，要根据实际情况定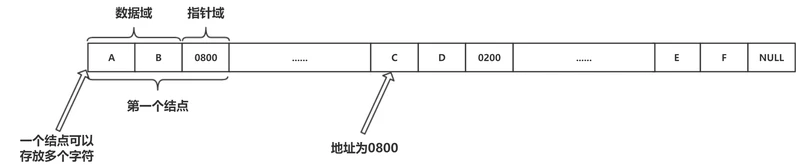

但是串中的字符都是连续存储的，而且串的操作不是插入、删除，所以字符串一经创建就是不变的，所以一般不用去考虑串的链式存储结构

五：关于串的匹配算法

例如我们需要从"ABCDEFG"这个主串中找到"EFG"这个子串的位置

 //比较好理解的写法，但是时间复杂度较大 static int IndexOf(string s1, string s2, int index = 0) { for (int i = index; i <= s1.Length - s2.Length; i++) { bool isEqual = true; for (int j = i; j < i + s2.Length; j++) { //注意要匹配的串每次都要从下标0开始比较（s2[j-i]） if (s1[j] != s2[j - i]) { isEqual = false; break; } } if (isEqual) { return i; } } return -1; }

 //朴素的模式匹配算法的另一种写法 static int IndexOf(string s1, string s2, int index = 0) { int i = index; int j = 0; while (i <= s1.Length - 1 && j <= s2.Length - 1) { if (s1[i] == s2[j]) { i++; j++; } else { i = i - j + 1; j = 0; } } if (j == s2.Length) { return i - s2.Length; } else { return -1; } }

引言：对于以上的算法，假如我们的主串为"00000.....000001"(前面有49个0)，要匹配的串为"0000000001"，那么每次都要循环到最后一位才发现这次查找是不匹配的，直到第41次循环才找到正确的匹配项，若使用朴素的模式匹配算法则需要执行40*10+10=410次，使用这个算法简直太低效了！而且对于计算机中，处理的都是0和1的串，万一出现以上的情况，还是得说一遍，这个算法太低效了！！！！！

有三位前人无法忍受朴素的模式匹配算法的低效，所以发明了一个新的模式匹配算法，我们把它称为克努特—莫里斯—普拉特算法，简称KMP模式匹配算法

六：实现串的顺序存储结构

using System; public class StringDS { //存储串中字符的字符数组 private char[] charArray; //串的长度 public int Length { get { return charArray.Length; } } //构造器初始化 public StringDS() { charArray = null; } public StringDS(char[] charArray) { this.charArray = new char[charArray.Length]; for (int i = 0; i < charArray.Length; i++) { this.charArray[i] = charArray[i]; } } public StringDS(string s) { this.charArray = new char[s.Length]; for (int i = 0; i < charArray.Length; i++) { this.charArray[i] = s[i]; } } //判断是否为空串 public bool IsNull() { return Length == 0; } //得到元素（通过索引器） public char this[int index] { get { if (index >= 0 && index <= Length - 1) { return charArray[index]; } else { throw new Exception("索引超出范围"); } } } //字符串连接 public static string Concat(StringDS s1, StringDS s2) { string str = ""; int len = s1.Length + s1.Length; for (int i = 0; i < len; i++) { if (i <= s1.Length - 1) { str += s1[i]; } else { str += s2[i - s1.Length]; } } return str; } //比较两个字符串大小 public int Compare(StringDS s) { int len1 = this.Length; int len2 = s.Length; int len = len1 > len2 ? len2 : len1; int index = -1; for (int i = 0; i < len; i++) { if (this[i] != s[i]) { index = i; break; } } if (index == -1) { if (len1 == len2) { return 0; } else { return len1 > len2 ? 1 : -1; } } else { return this[index] > s[index] ? 1 : -1; } } //找到一个字符串的子串 public string FindSubString(int index, int length) { string str = ""; if (index + length >= 0 && index + length <= this.Length - 1) { for (int i = index; i < index + length; i++) { str += charArray[i]; } return str; } else { throw new Exception("索引超出范围"); } } //将字符数组变为字符串输出 public string ToString_() { string str = ""; for (int i = 0; i < charArray.Length; i++) { str += charArray[i]; } return str; } //匹配字符串位置 public int IndexOf(StringDS s, int index = 0) { int i = index; int j = 0; while (i <= this.Length - 1 && j <= s.Length - 1) { if (this[i] == s[j]) { i++; j++; } else { i = i - j + 1; j = 0; } } if (j == s.Length) { return i - s.Length; } else { return -1; } } //反向输出字符串 public string Reverse() { string str = ""; for (int i = charArray.Length - 1; i >= 0; i--) { str += charArray[i]; } return str; } //替换字符串 public string Replace(string oldStr, string newStr) { if (oldStr.Length == newStr.Length) { char[] temp = charArray; int index = IndexOf(new StringDS(oldStr)) == -1 ? -1 : IndexOf(new StringDS(oldStr)); if (index != -1) { for (int i = index; i < index + oldStr.Length; i++) { temp[i] = newStr[i - index]; } StringDS s = new StringDS(temp); return s.ToString_(); } else { throw new Exception("原字符串中找不到要替换的字符串"); } } else { throw new Exception("替换的字符串长度不符"); } } } class Program { //*进行测试* public static void Main(string[] args) { StringDS s = new StringDS("abcdefg"); StringDS.Concat(new StringDS("abc"), new StringDS("def")); s.Compare(new StringDS("abcp")); s.IndexOf(new StringDS("ef"), 3); s.FindSubString(0, 5); s.Reverse(); s.Replace("ab", "ss"); } }