作差法的基本步骤

编程笔记 • 2024-11-13 10:36 • 阅读 0

随机事件的概率是对大量的重复试验中随机事件的频率具有稳定性这一客观规律抽象的结果。实际上，不仅仅是随机事件的频率具有稳定性，大量随机现象的平均结果一般也具有稳定性，即不论个别随机现象的结果以及它们在进行过程中的个体特征如何，大量随机现象的平均结果与各个随机现象的特征无关。概率论中用来阐述大量随机现象平均结果的稳定性的理论称为大数定律。

1、伯努利大数定律

2、常用的几个大数定律

2.1、大数定律的一般形式

2.2、切比雪夫大数定律

注意，切比雪夫大数定律只要求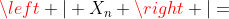 $\left | X_{n} \right |$ 互不相关（相互独立或互不相关），并不要求它们是同分布的。因此，很容易推出：如果 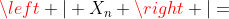$\left | X_{n} \right |$ 是独立同分布的随机变量序列，且方差有限，则 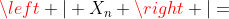$\left | X_{n} \right |$ 必定服从大数定律。伯努利大数定律是切比雪夫大数定律的特例。

2.3、马尔可夫大数定律

马尔可夫大数定律的重要性在于：对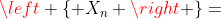 $\left \{ X_{n} \right \}$ 已经没有任何同分布、独立性、不相关的假定。切比雪夫大数定律显然可由马尔可夫大数定律推出。

2.4、辛钦大数定律

我们已经知道，一个随机变量的方差存在，则其数学期望必定存在；但反之不成立，即一个随机变量但数学期望存在，其方差不一定存在。以上几个大数定律均假设随机变量序列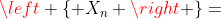 $\left \{ X_{n} \right \}$ 的方差存在，以下的辛钦大数定律去掉了这一假设，仅设每个 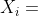$X_{i}$ 的数学期望存在，但同时要求 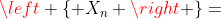$\left \{ X_{n} \right \}$ 为独立同分布但随机变量序列。伯努利大数定律也是辛钦大数定律但特例。

定理（辛钦大数定律）设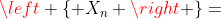 $\left \{ X_{n} \right \}$ 为一独立同分布但随机变量序列，若 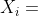$X_{i}$ 的数学期望存在，则 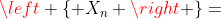$\left \{ X_{n} \right \}$ 服从大数定律，即对于任意的 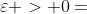$\varepsilon > 0$ ，下式成立：

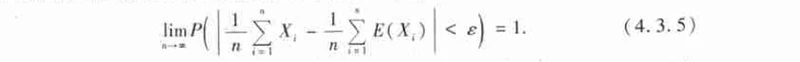
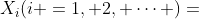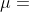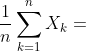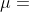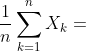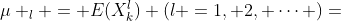由辛钦定理可知，如果随机变量 $X_{i}(i =1, 2, \cdots )$ 相互独立，服从同一分布且具有数学期望 $\mu$ ，则前n个随机变量的算术平均值 $\frac{1}{n}\sum_{k=1}^{n}X_{k}$ 依概率收敛于它们的数学期望 $\mu$ 。如果 $E(X_{k}^{l})=\mu _{l} (k =1, 2, \cdots )$ 存在，则 $\frac{1}{n}\sum_{k=1}^{n}X_{k}$ 依概率收敛于 $\mu _{l} = E(X_{k}^{l}) (l =1, 2, \cdots )$ 。这是在数理统计中求参数点估计的矩估计法的理论基础。