一、“根”的作用
“根”与系统中的“极点”相同。
拿一阶系统为例：
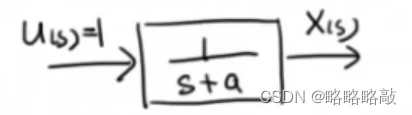
则：
令：
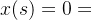
即，得根为：
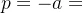
对x(s)进行Laplace逆变换，可得时间函数为：
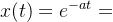,其中-a就是函数的“根”。
若a>0，则函数图像为指数衰减的形式：
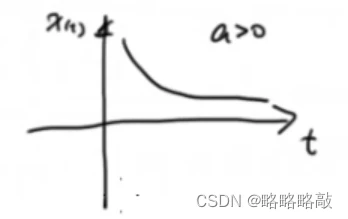
对于一般的一阶系统而言，若用复平面表示其系统的根，那一定落在实数轴上。
一阶系统中很多指标与“根”都息息相关，如时间常数、稳态时间等。
再拿二阶系统为例：
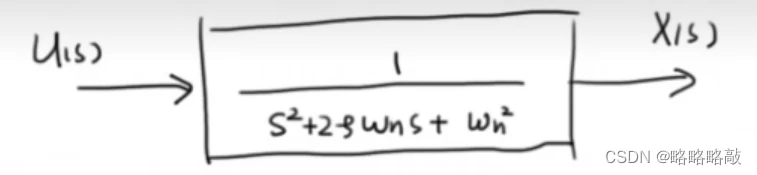
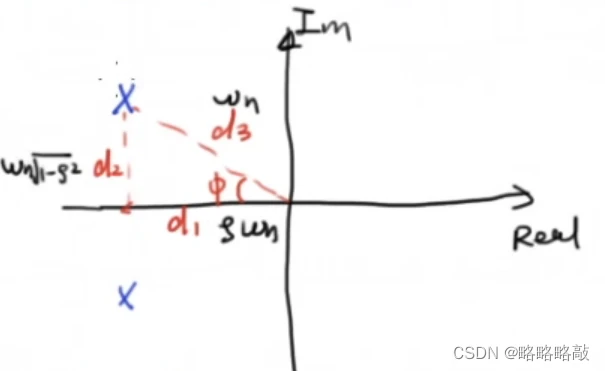
其中：固有频率：
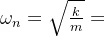
阻尼比：
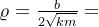
x(s)输出为
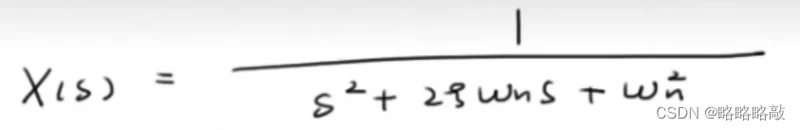
令分母为0，则：
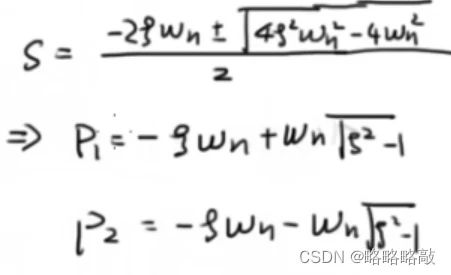
分类讨论：
i.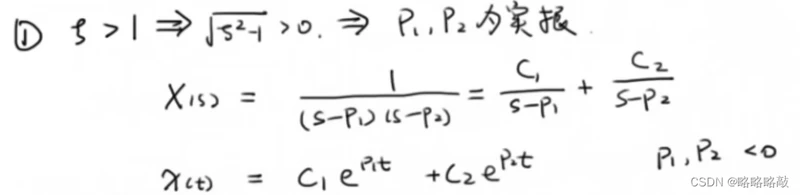
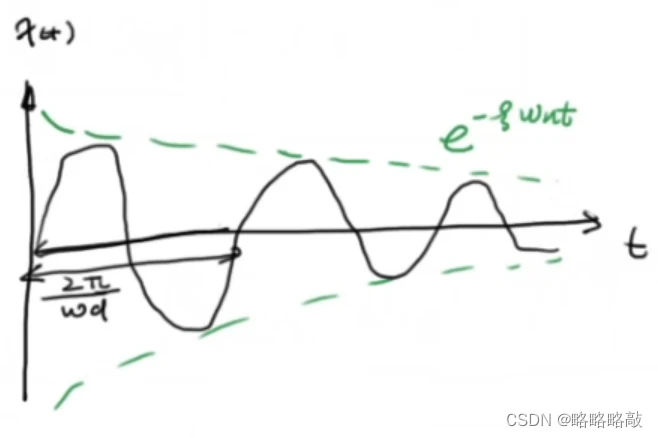
其系统图像：可看作两个一阶系统相加，有收敛程度缓的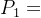
决定最终图像。
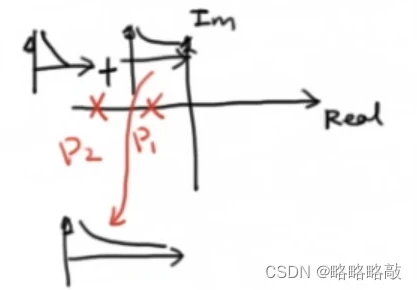
ii.
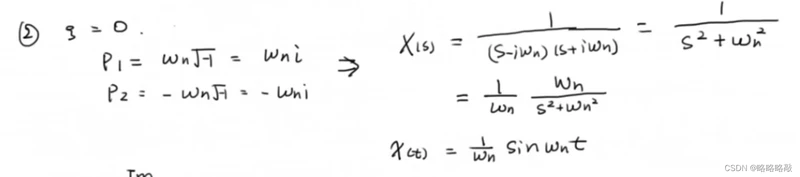
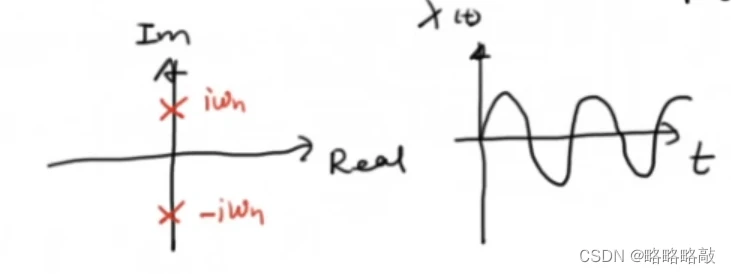
其系统图象：以
为频率的振荡图像
iii.
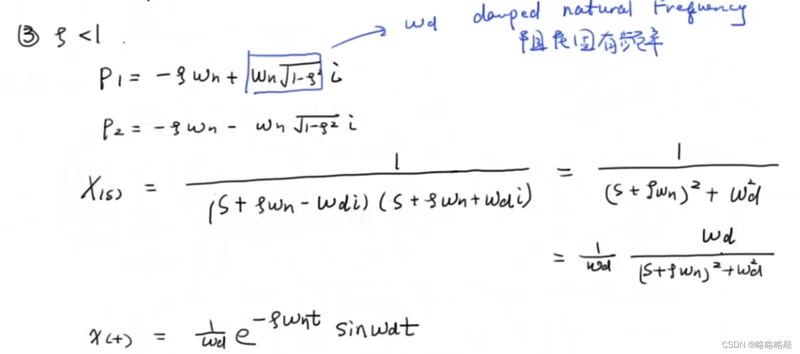
其系统图像：以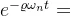
为渐近线的振荡图像
复平面图像：
二、“根”的手绘技巧
重点：
根轨迹的基本形式：
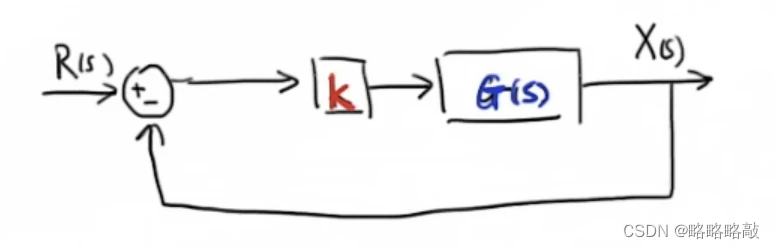
其传递函数表示为：其中我们研究的便是传递函数中的分母“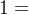
”时的根,当k从0到+
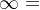时，闭环系统根位置变化的规律。
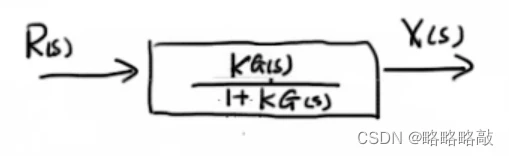
其中，我们是通过研究G(s)开环函数来对 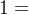的根进行分析。
对以下：
规则一：若m>n，则有m条根轨迹，
若n>m，则有n条根轨迹。
Eg：
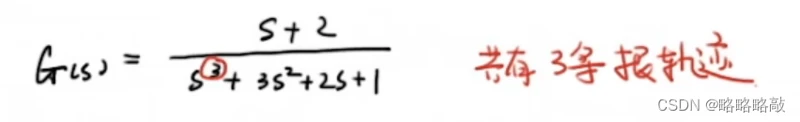
规则二：当m=n时，随着k从0到+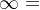，根轨迹从G(s)的极点向零点移动。即：
Eg：
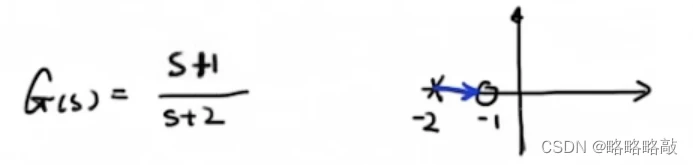
规则三：实轴上的根轨迹存在于从右向左数第奇数个极点/零点的左边
Eg：
规则四：若复数根存在，则一定是共轭的，所以根轨迹通过实轴对称。
规则五：若n>m，则有n-m个极点指向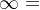
若n<m，则有m-n条根轨迹从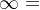指向零点
Eg：
规则六：根轨迹沿渐近线移动，渐进性与实轴的交点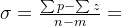
渐近线与实轴的夹角，其中
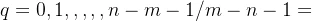
Eg:
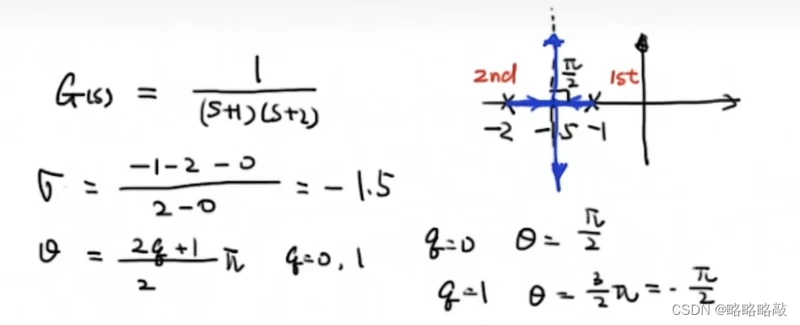
用MATLAB绘制根轨迹：
成功列出关于g的函数后，用rlocus()语句进行根轨迹的绘制，如：
则，根轨迹绘制图像：
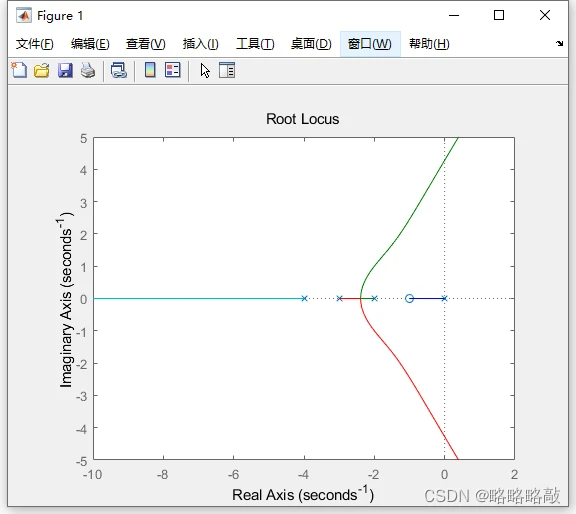
三、分离点/汇合点&根轨迹的几何性质
分离点/汇合点
定义：根轨迹在实轴上的汇合/分离的点则为汇合/分离点。
可通过求得系统中的极值来求得汇合点/分离点，其中最大值对应的是分离点，最小值对应的是汇合点。
根轨迹的几何性质
看以下例子：
其中：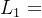
为零点长度，
、
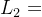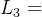为极点长度，
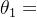为零点幅角，
、
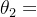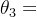为极点幅角（复数图像与x轴正方向形成的角度）。
G(s)的模为：
r=（所有零点长度的积）/（所有极点长度的积）
G(s)的幅角为：
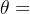=所有零点幅角的和 - 所有极点幅角的和
如以上的例子中：
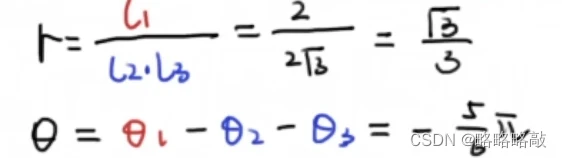
以上就是根轨迹的几何性质，可用于一个根轨迹中，判断一个根在根轨迹上，亦可以设定一个根加到这个根轨迹上。
