计算机常用进制及进制之间的转换
进制的由来
- 进制：进位计数制
- 原始的计数方式有：结绳计数、书契计数、算盘、正字记数法
生活中的常用进制
- 十进制
- 七进制：0~6
- 十二进制：0~11
- 百进制
- 千进制
计算机中的二进制
- 二数制：”莱布尼兹“发明
- 为什么采用二进制：电路简单，开代表“1”，关代表“0”。
- 将10个电路开关组合在一起，就是1024。
*
四种进制说明
- 常用进制：十进制、二进制、八进制、十六进制。
- 十进制：0~9，满10进1位，
- 二进制：0 1 ； 补码的形式保存，0b开头：例如 0b0100101
- 八进制：0~7 ，满8进1位，0开头 例如023
- 十六进制：0~9 ，A【10】 B【11】 C【12】 D【13】 E【14】 F【15】 0x开头 例如0x12AC
八进制和十六进制
-
为什么使用八进制和十六进制：为了二进制写法上的简便，将原来二进制的每三位放到一起组成一个八进制；将原来二进制的每四位放到一起组成十六进制。
-
-
在计算机中实际存储时，依然采用二进制进行存储
进制之间的转换
-
将其他进制转换为十进制
-
方法采用位权展开法：
-
将二进制转换十进制：
将对应位数上的数字和每一位的权重相乘，然后相加；底数为2
-
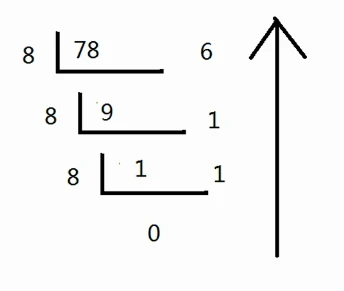
将八进制转换为十进制
-
将对应位数上的数字和每一位的权重相乘，然后相加。底数为8
-
-
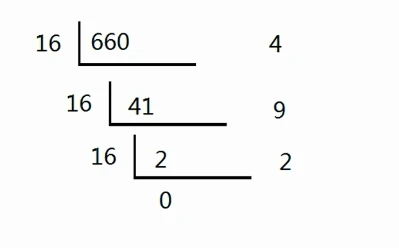
将十六进制转换为十进制
*
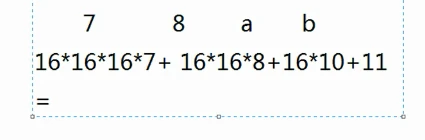将对应位数上的数字和每一位的权重相乘，然后相加。底数为16
-
-
-
将十进制转换为其他进制
-
方法1：短除法/除K逆取余法（K代表进制数 例如二进制就是2，八进制就是8。以此类推）
-
方法2：可以将十进制转换为二进制进而转换为八进制或十六进制（将原来二进制的每三位放到一起组成一个八进制；将原来二进制的每四位放到一起组成十六进制。）
-
将十进制转换为二进制
*
-
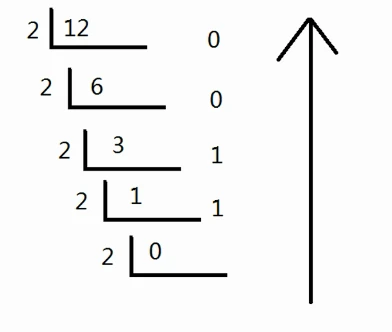
将十进制转换八进制
-
将十进制转十六进制
-
-
