六进制
一.进制转换
- 我们先看看十进制与二进制
(1)进制转换本质
我们使用短除法将十进制转换成二进制。
“数制”只是一套符号系统来表示指称“量”的多少。我们用“1”这个符号来表示一个这一“量”的概念。自然界的“量”是无穷的,我们不可能为每一个“量”都造一个符号,这样的系统没人记得住。所以必须用有限的符号按一定的规律进行排列组合来表示这无限的“量”。符号是有限的,这些符号按照某种规则进行排列组合的个数是无限的。十进制是10个符号的排列组合,二进制是2个符号的排列组合。
在进行进制转换时有一基本原则:转换后表达的“量”的多少不能发生改变。二进制中的111个苹果和十进制中的7个苹果是一样多的。
可以看出相邻的数位间相差进制的一次方。
进制这事儿,说到底就是位值原理,即:同一个数字,放在不同的数位上,代表不同大小的“量”。例如:十进制中,百位上的1表示100,十位上的1表示10。
任何进制中,每个数都可以按位权展开成各个数位上的数字乘以对应数位的位权,再相加的形式,如:
十进制的123=1×100+2×10+3×1
十进制的9876=9×1000+8×100+7×10+6×1
问:为啥相应的数位是1000、100、10、1?为啥不是4、3、2、1?
答:十进制,满十进一,再满十再进一,因此要想进到第三位,得有10×10;第4位得有10×10×10
这样我们就知道了:
对10进制,从低位到高位,依次要乘以10^0,10^1,10^2,10^3……,也就是1、10、100、1000
对2进制,从低位到高位,依次要乘以2^0,2^1,2^2,2^3……,也就是1、2、4、8、……
下面我们开始转换进制(以十进制换成二进制为例):
原来十进制咱们的数位叫 千位、百位、十位……
现在二进制数位变成了八位、四位、二位……
模仿上面十进制按位权展开的方式,把二进制数1011按权展开: 1011=1×2^3+0×2^2+1×2^1+1×2^0=1×8+0×4+1×2+1×1=8+2+1=11
接下来我们进行十进制往二进制的转换:
比较小的数,直接通过拆分就可以转换回去
比如13,我们把数位摆好八位、四位、二位,不能写十六了,因为一旦“十六”那个数位上的符号是“1”,那就表示有1个16,即便后面数位上的符号全部是“0”,把这个二进制数按权位展开后,在按照十进制的运算规律计算,得到的数也大于13了。那最多就只能包含“八”这个数位。 13-8=5,5当中有4,5-4=1
好啦,我们知道13=1*8+1*4+0*2+1*1 把“1”、“1”、“0”“1”这几个符号放到数位上去:
八位、四位、二位、一位
1 1 0 1
于是十进制数13=二进制数1101
想要知道其中的道理的话,请仔细品味以下的递归原理(不知道递归没关系):
一个十进制数321的末尾是1,意味着一定是……+1,省略号部分一定是10的倍数,所以一个十进制数末尾是1意味着十进制数除以进制10一定余1。所以第一次除以10之后的余数,应该放在十进制的最后一个数位“个位”,也就是说个位上的符号是1。
类比,一个二进制数111(注意,数值不等于上面十进制的111)末尾是1,意味着一定是……+1,前面的省略号部分都是2的倍数。所以一个二进制数末尾是1,意味着它对应的十进制数除以进制2一定余1。所以第一次除以2之后的余数,应该放在二进制的最后一个数位“一位”,也就是说一位上的符号是1。
如果一个十进制数321“十位”是2,我们希望把它转换为(1)的情况。那么我们把这个十进制数的末尾抹掉,也就是减去“个位”上的1,再除以进制10,得到32。这样原来“十位”上的“2”就掉到了“个位”上。再把32做(1)的处理。
类比,如果一个二进制数111“二位”是1,我们希望把它转换为(1)的情况,那么我们把这个二进制数的末尾抹掉,也就是减去“一位”上的1,再除以进制2,得到11。这样原来“二位”上的“1”就掉到了“一位”上。再把11做(1)的处理。
总结:其实这个过程就是把各个数位上的符号求出来的过程。
现在你应该可以回答以下问题了:为什么短除法可以实现进制的转换呢?为什么每次要除以进制呢?为什么要把余数倒着排列呢?
R进制转换成十进制就是按权位展开,把展开式放到十进制下,再按照“十进制”的运算规律计算。因为是十进制,所以就允许使用2、3、4、5、6、7、8、9了。所以2的n次方就不用写成指数,而可以用另外的八个符号来表示了。
(2)十进制--->二进制
对于整数部分,用被除数反复除以2,除第一次外,每次除以2均取前一次商的整数部分作被除数并依次记下每次的余数。另外,所得到的商的最后一位余数是所求二进制数的最高位。
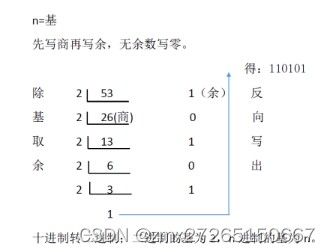
十进制转二进制
对于小数部分,采用连续乘以基数2,并依次取出的整数部分,直至结果的小数部分为0为止。故该法称“乘基取整法”。
给你一个十进制,比如:6,如果将它转换成二进制数呢?
10进制数转换成二进制数,这是一个连续除以2的过程:
把要转换的数,除以2,得到商和余数,
将商继续除以2,直到商为0。最后将所有余数倒序排列,得到数就是转换结果。
听起来有些糊涂?结合例子来说明。比如要转换6为二进制数。
“把要转换的数,除以2,得到商和余数”。

十转二示意图
那么:要转换的数是6, 6 ÷ 2,得到商是3,余数是0。
“将商继续除以2,直到商为0……”
现在商是3,还不是0,所以继续除以2。
那就: 3 ÷ 2, 得到商是1,余数是1。
“将商继续除以2,直到商为0……”
现在商是1,还不是0,所以继续除以2。
那就: 1 ÷ 2, 得到商是0,余数是1
“将商继续除以2,直到商为0……最后将所有余数倒序排列”
好极!现在商已经是0。
我们三次计算依次得到余数分别是:0、1、1,将所有余数倒序排列,那就是:110了!
6转换成二进制,结果是110。
把上面的一段改成用表格来表示,则为:
| 被除数 | 计算过程 | 商 | 余数 |
| 6 | 6/2 | 3 | 0 |
| 3 | 3/2 | 1 | 1 |
| 1 | 1/2 | 0 | 1 |
(在计算机中,÷用 / 来表示)
(3)二进制--->十进制
二进制数转换为十进制数
二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……
所以,设有一个二进制数:0110 0100,转换为10进制为:
下面是竖式:
0110 0100 换算成十进制
从右往左开始换算
第0位 0 * 2^0 = 0
第1位 0 * 2^1 = 0
第2位 1 * 2^2 = 4
第3位 0 * 2^3 = 0
第4位 0 * 2^4 = 0
第5位 1 * 2^5 = 32
第6位 1 * 2^6 = 64
第7位 0 * 2^7 = 0
公式:第N位2(N)
---------------------------
100
用横式计算为:
0 * 2^0 + 0 * 2^1 + 1 * 2^2 + 0 * 2^3 +0 * 2^4 +1 * 2^5 + 1 * 2^6+0 * 2^7 = 100
除0以外的数字0次方都是1,但0乘以多少都是0,所以我们也可以直接跳过值为0的位:
1 * 2^2 + 1 * 2^5 +1 * 2^6= 100
2.下面我们来讨论十进制与六进制的关系
(1)十进制--->六进制
十进制数转换成六进制的方法,和转换为二进制的方法类似,唯一变化:除数由2变成6。
来看一个例子,如何将十进制数120转换成六进制数。
用表格表示:
| 被除数
| 计算过程
| 商
| 余数
|
| 120 | 120/6 | 20 | 0 |
| 20 | 20/6 | 3 | 2 |
| 2 | 2/6 | 0 | 2 |
120转换为8进制,结果为:320。
(2)六进制--->十进制
六进制就是逢6进1。
六进制数采用 0~5这六数来表达一个数。
六进制数第0位的权值为6的0次方,第1位权值为6的1次方,第2位权值为6的2次方……
所以,设有一个八进制数:1505,转换为十进制为:401
用竖式表示:
1507换算成十进制。
第0位 5* 6^0 = 5
第1位 0 * 6^1 = 0
第2位 5 * 6^2 = 180
第3位 1 * 6^3 = 216
二.算法实现
1.输入十进制n的值:
n=int(input())2.利用函数求六进制
(1)定义了一个名为 a 的函数,该函数接受一个整数参数 n。
(2)在函数内部,定义了一个字符串 m,它包含了六进制数的字符表示:'012345',这是六进制数字0到5的字符表示。
(3)初始化一个空字符串 i 用于存储六进制表示。
(4)检查如果 n 等于0,就返回字符串 '0',因为六进制中0表示为0。
(5)使用一个 while 循环,不断执行以下步骤,直到 n 变为0: a. 计算 n 对6取余,将余数存储在变量 liu 中。 b. 将 liu 对应的六进制字符从字符串 m 中取出,并将它附加到字符串 i 的前面。 c. 将 n 除以6并取整数部分,更新 n 的值。
(6)最终,当 n 变为0时,i 中包含了 n 的六进制表示。
代码如下:
def a(n):
m = '012345'
i = ''
if n==0:
return '0'
while n:
liu=n%6
i=m[liu]+i
n=n//6
return i3.打印六进制的值
print(a(n))4.全部代码如下:
n=int(input())
def a(n):
m = '012345'
i = ''
if n==0:
return '0'
while n:
liu=n%6
i=m[liu]+i
n=n//6
return i
print(a(n))