在之后的项目中有编写复数函数的要求，所以先总结资料以备用。同时也发布在这里以供大家参考。
复数的加法运算
(a+bi)+(c+di)=(a+c)+(b+d)i
复数的减法运算
(a+bi)-(c+di)=(a-c)+(b-d)i
复数的乘法运算
(a+bi)(c+di)=(ac-bd)+(bc+ad)i
复数的除法运算
(a+bi)/(c+di)
=(ac + bd)/(c^2 + d ^2) +((bc - ad)/(c ^2 + d ^2)) i
复数的指数运算
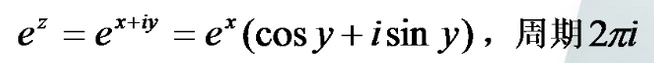
复数的log运算
θ = carg(z) = atan2(y, x),
log(z) = log(r exp(θi)) = log® + θi.
对于以其它数为底的对数，可以使用换底公式：
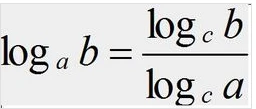
复数的幂运算
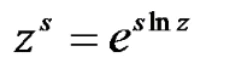复数的幂运算单独进行，比较复杂。可以在指数运算和对数运算的基础上进一步进行。
求复数的cos函数值
由 cos(a+b) = cosacosb - sinasinb 得
cos(a+bi) = cosacos(bi) - sinasin(bi)
又
sinh x = -i sin(i * x)
cosh x = cos(i * x)
tanh x = -i tan(ix)
coth x = i cot(i * x)
sech x = sec(i * x)
csch x = i csc(i * x)
所以
cos(a+bi)
= cosacos(bi) - sinasin(bi)
= cosacoshb + [sina*sinhb] i
求复数的sin函数值
由 sin(a+b) = sinacosb + cosasinb 得
sin(a+bi) = sinacos(bi) + cosasin(bi)
又
sinh x = -i sin(i * x)
cosh x = cos(i * x)
tanh x = -i tan(ix)
coth x = i cot(i * x)
sech x = sec(i * x)
csch x = i csc(i * x)
所以
sin(a+bi)
= sinacos(bi) + cosasin(bi)
= sinacoshb - [cosa*sinhb] i
也可以使用此公式，在指数运算的基础上进行。
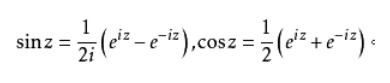
复数的n次开方运算
任意复数表示成 z = a + bi
若 a = ρcosθ, b = ρsinθ, 即可将复数在一个平面上表示成一个向量, ρ为向量长度（复数中称为模）,θ为向量角度（复数中称为辐角）
即 z = ρcosθ + ρsinθ, 由欧拉公式得 z = ρe^(iθ)
注意到向量角度, cos(2kπ+θ) = cosθ, sin(2kπ+θ) = sinθ
所以 z = ρe^ (iθ) = ρe^[i(2kπ+θ)
开n次方,z^ (1/n )= ρ^ (1/n) * e^ [i(2kπ+θ)/n]
k=0,1,2,3……n-1,n,n+1……
k=n时,易知和k=0时取值相同
k=n+1时,易知和k=1时取值相同
故总共n个根,复数开n次方有n个根
故复数开方公式
先把复数转化成下面形式
z = ρcosθ + ρsinθ = ρe^[i(2kπ+θ)
z^ (1/n) = ρ^ (1/n) * e^ [i(2kπ + θ)/n]
k取0到n-1。
然后再通过指数运算求值。
复数的反三角函数运算
复数的双曲函数运算
根据转换，转换成复数的指数运算。
初次撰写博客，多有瑕疵敬请指教。
