中心性(Centrality)是社交网络分析(Social network analysis, SNA)中用以衡量网络中一个点或者一个人在整个网络中接近中心程度的一个概念,这个程度用数字来表示就被称作为中心度。也就是说,通过了解一个节点的中心性,从而判断这个节点在网络中所占据的重要性。
在图论和网络分析中,中心性指标可确定图中的最重要节点。 其应用包括识别社交网络中最有影响力的人,互联网或城市网络中的关键基础设施节点以及疾病的超级传播者。
中心性算法主要用于识别图中特定节点的角色及其对网络的影响。对于节点重要性的解释有很多种,不同的解释下判定中心性的度量指标也有所不同,但当前最主要的度量指标为点度中心性(Degree Centrality)、接近中心性(Closeness Centrality)、中介中心性(Between Centrality) 、特征向量中心性(Eigenvector Centrality)四种。
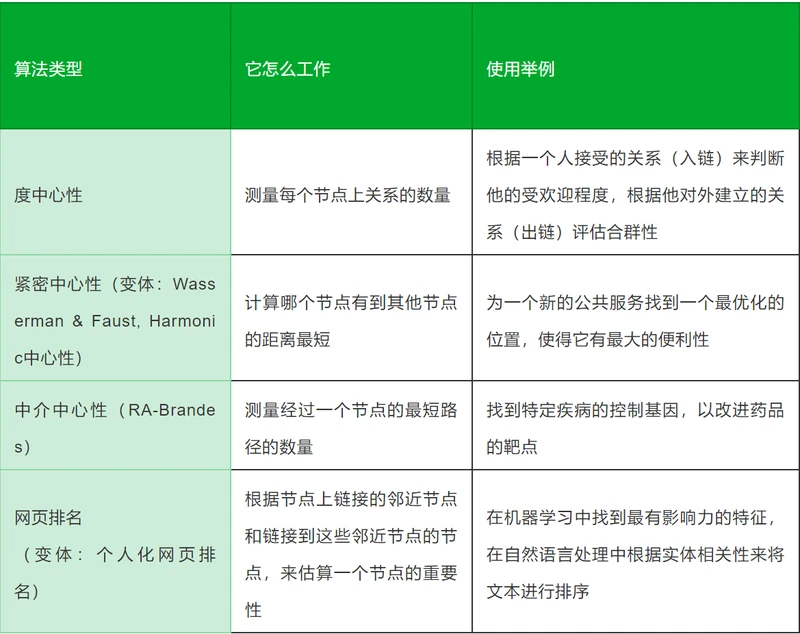
(1)度中心性(Degree Centrality):度中心性测量网络中一个节点与所有其它节点相联系的程度。
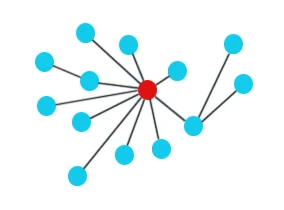
在无向图(Undirected Graph)中,度中心性测量网络中一个节点与所有其它节点直接相连的程度。对于一个拥有g个节点的无向图,节点i的度中心性是i与其它g-1个节点的直接联系总数(如果是有向图,则需要考虑的出度和入度的问题):
C
D
(
N
i
)
=
∑
j
=
1
g
x
i
j
(
i
≠
j
)
C_D(N_i)=\sum_{j=1}^{g}x_{ij} (i≠j)
CD(Ni)=j=1∑gxij(i=j)
由上述公式可见,网络规模越大,度中心性的最大可能值就越高。为了消除网络规模变化对度中心性的影响,需要进行标准化:
C
D
’
(
N
i
)
=
C
D
(
N
i
)
g
−
1
C_D’(N_i)=\frac{C_D(N_i)}{g-1}
CD’(Ni)=g−1CD(Ni)
在这个标准化度中心性测量公式中,使用节点i的度中心性值除以其它g-1个节点最大可能的连接数,得到与节点i有直接联系的网络节点的比例。这个比例越大,则表明其中心性越高。
【示例】在一场有50人的派对里,A与其中的30人相识,而B只与其中的10人相识。在派对人数规模一样的情况下,根据相识的人数。可以看得出来A的社交圈子要比B更加广,也就是说A的度中心性高于B,即
C
D
(
A
)
=
30
50
=
0.6
>
C
D
(
B
)
=
10
50
=
0.2
C_D(A)=\frac{30}{50}=0.6>C_D(B)=\frac{10}{50}=0.2
CD(A)=5030=0.6>CD(B)=5010=0.2
(2)接近中心性(Closeness Centrality):接近中心性反映在网络中某一节点与其他节点之间的接近程度。不同于度中心性考虑直接相连的情况,接近中心性需要考量每个结点到其它结点的最短路径的平均长度。也就是说,对于一个结点而言,它距离其它结点越近,那么它的中心度越高。
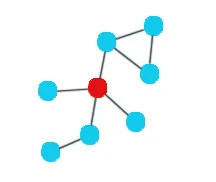
计算方式如下:
C
C
(
N
i
)
=
1
∑
j
=
1
g
d
i
s
(
i
,
j
)
C_C(N_i)=\frac{1}{\sum_{j=1}^{g}dis(i,j)}
CC(Ni)=∑j=1gdis(i,j)1
其中dis(i,j)表示节点i到节点j的距离。
之所以对距离和取倒数,是为了方便表示,因为这样就可以直观地表示为:
C
C
C_C
CC值越大,其接近中心性越高。
在刚刚我们说到要考量最短路径的平均长度,更常见的表示方法是将此分数标准化,使其表示最短路径的平均长度,而不是它们的和。标准化的接近中心性计算公式如下:
C
C
′
(
N
i
)
=
g
−
1
∑
j
=
1
g
d
i
s
(
i
,
j
)
C_C'(N_i)=\frac{g-1}{\sum_{j=1}^{g}dis(i,j)}
CC′(Ni)=∑j=1gdis(i,j)g−1
由上述公式可见,如果节点到图中其它节点的最短距离都很小,那么我们可以认为该节点的接近中心性较高。显然,这个定义比度中心性在几何上更符合中心性的概念,因为到其它节点的平均最短距离最小,意味着这个节点从几何角度看是位于图的中心位置。
【示例】在建立商业活动中心的时候,往往需要考虑选址问题,我们希望四面八方的顾客到商业中心来的路程都较短,那么利用接近中心性这一度量,可以很好地找到一个距离其他地点都较近的建址。
(3)中介中心性(Between Centrality) :中介中心性用于衡量一个顶点出现在其他任意两个顶点对之间的最短路径的次数,从而来刻画节点重要性。中介中心性测量了某个节点在多大程度上能够成为“中介”,即在多大程度上控制他人。如果一个节点处于多个节点之间,则可以认为该节点起到重要的“中介”作用,处于该位置的人可以控制信息的传递而影响群体。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lfdOWUgr-1615800849105)(https://imgkr2.cn-bj.ufileos.com/74d70fbf-3b78-45d9-9c7a-912494feb6df.png?UCloudPublicKey=TOKEN_8d8b72be-579a-4e83-bfd0-5f6ce1546f13&Signature=28PPVCDAF5SbenxLQ4H4wAbe9DQ%253D&Expires=1615884674)]](https://yyzqsoft.com/uploads/202407/04/9a52744a53e9d4a7.webp)
计算方式如下:
C
B
(
N
i
)
=
∑
j
,
k
=
1
g
s
d
(
j
,
i
,
k
)
,
(
j
≠
k
)
C_B(N_i)=\sum_{j,k=1}^{g}sd(j,i,k),(j≠k)
CB(Ni)=j,k=1∑gsd(j,i,k),(j=k)
其中sd(j,i,k)表示j到k的最短路径经过了i,即i处于j到k的最短路径上。
同样地,可以对
C
B
(
N
i
)
C_B(N_i)
CB(Ni)进行标准化:
C
B
′
(
N
i
)
=
C
B
(
N
i
)
∑
j
,
k
=
1
g
(
j
,
k
)
,
(
j
≠
k
)
C_B'(N_i)=\frac{C_B(N_i)}{\sum_{j,k=1}^{g}(j,k)},(j≠k)
CB′(Ni)=∑j,k=1g(j,k)CB(Ni),(j=k)
其中分母表示图中两点间路径的条数,即所有路径的数量。
【示例】主要用于衡量一个顶点在图或网络中承担“桥梁”角色的程度,该中心性经常用于反欺诈场景里中介实体的识别。例如,婚介所的媒人,同样可以视为“桥梁”。社交圈子里的社交达人,也是如此。
(4)特征向量中心性(Eigenvector Centrality):一个节点的重要性既取决于其邻居节点的数量(即该节点的度),也取决于其邻居节点的重要性。
假设
x
i
x_i
xi表示节点i的重要性,则特征向量中心性计算如下:
C
E
(
N
i
)
=
x
i
=
c
∑
j
=
1
g
a
i
j
x
j
C_E(N_i)=x_i=c\sum_{j=1}^{g}a_{ij}x_j
CE(Ni)=xi=cj=1∑gaijxj
其中
c
c
c为一个比例常数,
a
i
j
=
1
a_{ij}=1
aij=1当且仅当i与j相连,否则为0。
PageRank算法是特征向量中心性的一个变种,关于PageRank的详情可以参考我的文章浅谈PageRank算法。
参考文献:
https://blog.csdn.net/myy3075/article/details/87948777
https://mp.weixin.qq.com/s/mydBp18Shm5K5EujOFNrvw
