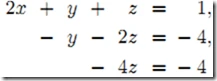高斯消元法，是线性代数中的一个算法，可用来求解线性方程组，并可以求出矩阵的秩，以及求出可逆方阵的逆矩阵。
高斯消元法的原理是：
若用初等行变换将增广矩阵 化为 ，则AX = B与CX = D是同解方程组。
所以我们可以用初等行变换把增广矩阵转换为行阶梯阵，然后回代求出方程的解。
1、线性方程组
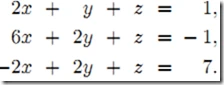
1）构造增广矩阵，即系数矩阵A增加上常数向量b（A|b）
2）通过以交换行、某行乘以非负常数和两行相加这三种初等变化将原系统转化为更简单的三角形式（triangular form）
注：这里的初等变化可以通过系数矩阵A乘上初等矩阵E来实现
3）从而得到简化的三角方阵组，注意它更容易解
4）这时可以使用向后替换算法（Algorithm for Back Substitution）求解得
z=-4/-4=1, y=4-2z=4-2=2, x= (1-y-z)/2=(1-2-1)/2=-1
总结上面过程，高斯消元法其实就是下面非常简单的过程
原线性方程组 ——> 高斯消元法 ——> 下三角或上三角形式的线性方程组 ——> 前向替换算法求解（对于上三角形式，采用后向替换算法）
补充1：
高斯－若尔当消元法（Gauss-Jordan Elimination）
相对于高斯消元法，高斯－若尔当消元法最后的得到线性方程组更容易求解，它得到的是简化行列式。其转化后的增高矩阵形式如下，因此它可以直接求出方程的解，而无需使用替换算法。但是，此算法的效率较低。
例子如下：
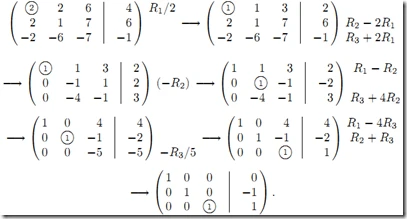解为
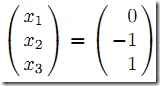
个人感觉区别就是对每行进行了归一化处理
补充2：
介绍了最基本的高斯消元法，现在看看应用于实际问题的实用算法
因为实际应用中，我们总是利用计算机来分析线性系统，而计算机中以有限的数来近似无限的实数，因此产生舍入误差（roundoff error），进而对解线性系统产生很多影响。
一个t位（即精度为t）以
为基的浮点数的表达形式为：
，
。对于一个实数x，其浮点近似值
为最接近x的浮点数，必要时进行近似
