一、柯西不等式
1、基本介绍
设 ,
,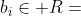 ,其中
,其中 ,则
,则 ,取等时,
,取等时,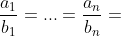 ,即
,即 。
。
2、证明
取向量 ,
, 。
。
因为 ,
,
 ,
, 。
。
所以 成立,取等时
成立,取等时 ,此时
,此时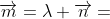 ,
, 。
。
根据以上的证明所得 ,我们可以将柯西不等式理解为:两个向量的内积的模长的平方,小于等于两者模长的平方的积。
,我们可以将柯西不等式理解为:两个向量的内积的模长的平方,小于等于两者模长的平方的积。
3、向量的柯西不等式
以上的柯西不等式,其实是向量柯西不等式在代数上的推广,向量的柯西不等式有: 。
。
证明:根据余弦函数的性质,对任意的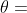 ,有
,有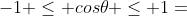 ,两边同时乘以
,两边同时乘以 ,有
,有 。
。
两个向量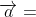 、
、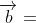 的大小固定时,有下图(1)、(2)、(3) 的 3 种关系。
的大小固定时,有下图(1)、(2)、(3) 的 3 种关系。
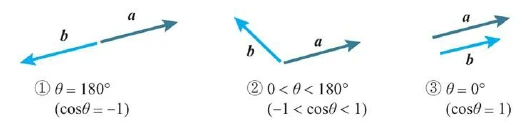
根据柯西 - 施瓦茨不等式 (3),可以得出以下性质:
-
当两个向量方向相反时,内积取得最小值。
-
当两个向量不平行时,内积取平行时的中间值。
-
当两个向量方向相同时,内积取得最大值。
性质①就是梯度下降法的基本原理。
另外,可以认为内积表示两个向量在多大程度上指向相同方向。如果将方向相似判定为“相似”,则两个向量相似时内积变大。我们考察卷积神经网络时,这个观点就变得十分重要。

