VSO:Visual Semantic Odometry（ECCV 2018）

推荐另外三篇视觉语义里程计论文：

. 《Probabilistic Data Association for Semantic SLAM》 ICRA 2017 宾夕法尼亚大学
. 《Stereo Vision-based Semantic 3D Object and Ego-motion Tracking for Autonomous Driving》 ECCV 2018 港科大
. 《Long-term Visual Localization using Semantically Segmented Images》ICRA 2018
vso- 苏黎世联邦理工；svo-苏黎世大学；slam++， SemanticFusion-英国帝国理工学院。
摘要
    该篇论文提出了一种用语义信息实现中期连续点跟踪的方法。可以被简单地融合进已有的直接或间接视觉里程计框架中。在自动驾驶下应用该方法实现了巨大改善。

1. Introduction
        为了减小积累的误差，相关观测图像之间的关联用于联合估计姿态和地图。有两种正交方法：
        第一种使用图像之间的短期关联来获得暂时的漂移校正，通过过渡性地建立连续相机帧之间的约束。这种方法在车辆长期在直线公路上前进时非常有效。
    第二种通过回环检测在远帧之间建立长距离约束。这种情况适用于相机重复访问之前的位置，或者基于建立好的地图定位的情况。
         本文提出利用语义信息来改善第一种漂移校正策略，建立点的中期连续跟踪。目前自动驾驶领域的一流方案中都缺少不变量的呈现：无论是基于特征的ORB-SLAM还是直接法的LSD-SLAM或者DSO，不能连续跟踪一个点持续很长距离。因为它们的呈现对视角和光照变化并不鲁棒。

Fig.1. 追上前面的车辆过程中，跟踪的Patch由于尺度变化后跟踪失效，但语义信息一直保持一致。

        由于图1中的问题，该场景下的沿着路走的车辆无法实现中期跟踪。
        论文的主要思想为使用语义作为不变的场景呈现元素。潜在假设为视角、尺度、光照的变化仅仅影响低等级的物体表观，而不影响它们的语义含义。本文提出独特的visual semantic odometry (VSO) 来整合语义约束到姿态和地图优化中。
        论文的贡献如下：
        1） 推导一种独特的最小化语义投影误差的损耗函数，而且发现可以使用期望最大化（EM）法最小化。可以与任何语义分割算法结合。
        2） 将语义误差项整合到VO算法中显著改善自动驾驶场景的平移漂移问题。
        3） 我们做了实验分析什么条件下有改善，并讨论当前限制。

2. Related Work
        视觉里程计系统可以这样分类：滤波或非滤波优化，稀疏或稠密，直接或间接。论文旨在提出应用语义误差项改善数据关联。因此，论文提出的方法和现有的VO方法不太一样，它们大部分使用语义来做VO或者做图像-模型关联。
        直接法 最小化相邻帧相关像素的光度误差。由于能量函数基于图像梯度，因此很需要好的相机初始化姿态和场景结构来收敛。作者一再强调光度误差度量对小的视角和光照变化不鲁棒。大部分直接法都只能短时间内跟踪，引入语义使得跟踪范围加大。
        间接法 最小化3D地图点到观测图像中的投影误差。间接VO一般使用特征匹配建立稀疏的联系，因此对视角和光照变化更加鲁棒。由于其局部性质，特征检测和描述子对大的变化并不能适应。因此和直接法的局限性差不多。
        语义建图 基于已知姿态从图像中建立语义3D地图。地图通过固定相机位置来联合推断语义和几何信息来建立，论文的方法也建立了语义标注的3D地图作为副产品。但论文专注于联合优化语义、几何和相机姿态。
        语义视觉里程计方法 使用更高等级特征，如线、平面或物体来改善VO鲁棒性或获得更丰富的地图呈现。该部分详细论述了一下，Bowman 的《probabilistic data association for semantic slam》提出概率关联模型来避免硬决策，与之对比，作者的论文不需要离散数据关联，它通过考虑物体边界的连续距离来获得，而不是仅仅是独立的物体检测。(In contrast, our approach does not need a discrete data association by considering continuous distances to object boundaries rather than individual object detections)
        通过聚焦于语义物体边界，我们可以处理很多语义物体。比如，我们既可以利用凸物体，还有不能被矩形框描述的物体，如街道、天空、建筑。
        语义图像-模型匹配 有人分割三维物体，通过将物体投影到2d分割图像中。同时期作品中，有将语义标注的3d点投影到语义分割图像中的。它们需要一个事先建立并标记的3d模型，作为对比，文中是为VO设计。

3. Visual Semantic Odometry
3.1. Visual Semantic Odometry Framework
        一些基本的符号定义：
        . 输入图像

        . 相机姿态

，其中​$T_k\in SE(3)$.
        . 地图点

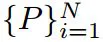
        首先基本的里程计目标函数为：

        其中​$e_b$${}_a$${}_s$${}_e(k,i)$表示在第$k$个相机下看到的第$i$个点的cost。要么被定义为光度差异（直接法）或者几何差异（间接法）。由于作者表示提出的语义方法可以基于原来的方法改善，所以该公式即为原本算法的误差模型。重点在于接下来的语义模型。
        对于输入图像，进行语义分割，得到稠密的，每个点都有类别的分类图像。因而每个地图点除了3d位置，也包含了分类信息。
         定义$w_i^{(}$${}^c$${}^{)}$来表示点$P_i$属于分类$c$的概率，该参数将在后面详细论述。

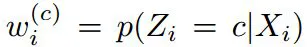
        定义语义cost function，每一项联系了相机姿态Tk和地图点$P_i$：

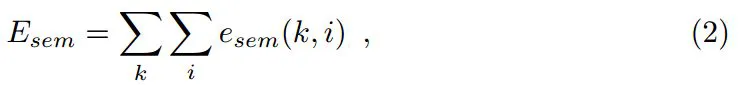
        因此构造了优化对象，结合基础算法的目标函数和新增的语义项目标函数：

        而​$\lambda$则作为权重，与语义的可信度有关。而语义的可信度取决于分类器的效果和场景影响，在后文详细论述。
3.2. Semantic Cost Function
        首先，该部分的核心思想其实很简单，即我们要衡量该姿态的相机观测得到的语义分类和地图的语义关系能多好地匹配。匹配方式则是将地图的点，按照当前相机的姿态，投影到成像平面中（类似BA，只是BA比较的是RGB而已）。对应成像平面的位置如果分类就是地图中点的分类，那就概率取高，那么如果不是呢？便定义一个方法以最近正确分类来表示这个概率，即下文将描述的DT。

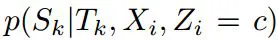
        定义观测似然，该公式表示将地图点投影到图像$S_k$中，对应的位置标签为$c$的概率。投影与最近标记为c的点距离越远则概率越低。这里定义了一个$Distancetransform-DT$.
$D{T}_B(p)$：$R^2——>R$，其中$p$是像素位置，$B$是二值图像。

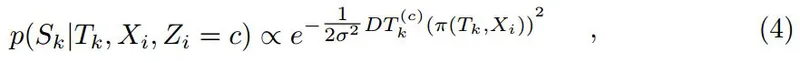
        根据Fig.2. 语义似然推断的阐述。输入语义分割图（a），取出分类为车辆的部分到图（b），语义似然（$\sigma =10$​）和（$\sigma =10$​）的情况分别见图（c），（d）。红色代表1，蓝色代表0.
        即公式用高斯分布的方式来将距离转化成了概率。

    几个细节：1） $\sigma$ ​表示语义图像分类的不确定度。 2） 公式4的详细推导可见附加材料。

        该部分可以参考激光模型中的似然域模型。

        结合Eq.4，我们可以定义语义误差项：

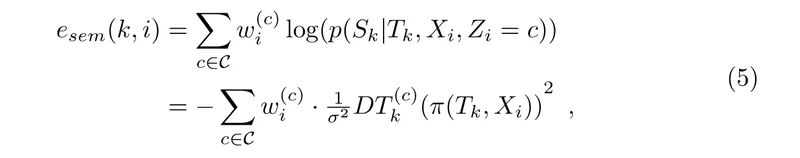
        其中​$\pi (T_k,X_i)$用相机姿态$T_k$将点$P_i$投影到语义分割图像$S_k$中。
        $w_i^{(}$${}^c$${}^{)}$表示​$P_i$是类别$c$的概率，而且会随着观测实时更新。论文中说“直观上该公式是2D距离的权重平均”。2D距离，即到最近正确分类点$P_i$的2D像素距离。又举了个例子说：如果点​$P_i$分类为人行道和马路的概率相同，那么它的误差项将在二者的分界上取得最小值。
        $w_i^{(}$${}^c$${}^{)}$ 的实时随观测更新表现在哪呢。具体来说，点的标签概率向量​$w_i$​联合考虑所有观测来计算。如果点$P_i$被一组观测量观测，那么：

        常量用于确保:

        所以每次能看到$P_i$的观测，得到的其分类为$c$的概率将被乘上去来改变$w_i^{(}$${}^c$${}^{)}$，规则允许通过积累观测数据增量式更新标签向量​$w_i$。而如果大部分观测值们对于同一个分类有最大值，那么该类别$c$整体的乘积也将相对于其他错误分类收敛到一个尖峰值去。
        最后解释一下Eq.5中的参数​$\sigma$非常重要，假设一个地图点投影到了Fig2中car分类的外面，我们假设只有两个分类：car和no_car。这个点在$c$=car的时候的​$w_i^{(}$${}^c$${}^a$${}^r$${}^{)}=1$ 。那么根据公式5，剩余部分将与​的值成反比(怎么不是负反比)。而且如果$\sigma$大的话，Eq.4中分类似然几乎会是单调的（因为是个高斯分布，方差大的时候分布非常宽），于是导致语义项对点分类的影响无效了。比如与物体边界相近？？？
3.3 Optimization
        该部分论述如何求解上述模型。使用expectation maximization (EM) 法，分E、M两步分别求解。
        E-step ： 对每个点P_i计算权重向量，同时保持点位置和相机姿态固定。
        M-step ：反过来优化点的位置和姿态，但固定权重。
        由于E_sem含有稀疏结构，M-step使用Levenberg-Marquardt算法求解
。
        给出的优化框架能够通过将点标签$Z_i$作为潜在变量并最大化似然推导出。
        仅仅使用语义信息会使得约束过少，公式四（DT）在物体内部是均匀分布。

        如左图所示，语义的解有很多。为了避免这种情况，作者提了四点：
        1） 语义优化联合基本视觉里程计功能一起
        2） 使用多个点和语义约束优化单独相机姿态
        3） 仅仅提供语义约束而不提供基本约束的点，如不会再被基本系统优化的点，将被固定并且仅仅相关的相机姿态会被优化来减小漂移。这个过程不光限制了优化变量的数量，并且提供了点之间的结构关联，因而约束了姿态解。如右图。
        4） 通过高频的语义优化，我们减少了将点匹配到错误物体情况的概率，由于优化基于DT的梯度，我们假设点会在正确标记区域附近，所以会把点拉向正确区域。
3.4 Obtaining Semantic Constraints & System Integration
        除了语义系统外还有基本的视觉里程计系统。可选用直接法或间接法。对每帧生成一张可视点V(k)，其中每个点可建立可优化的相机-点约束。每一帧还生成语义可见列表V_sem(k)，如果点i的投影足够接近该点的语义区域，那么将被插入到V_sem(k)中。
        VO方法有active window来用一部分帧优化轨迹，我们也定义了active semantic window存放语义关键帧。一旦一帧离开AW，就将其加入到ASW。ASW中帧的姿态不再被优化，因为它们缺少与当前帧的光照/尺度约束。
        补充材料更加详细地描述了如何从存在的VO框架中获得语义关系，以及整合论文方法到已存在系统中。

4. Experimental Evaluation
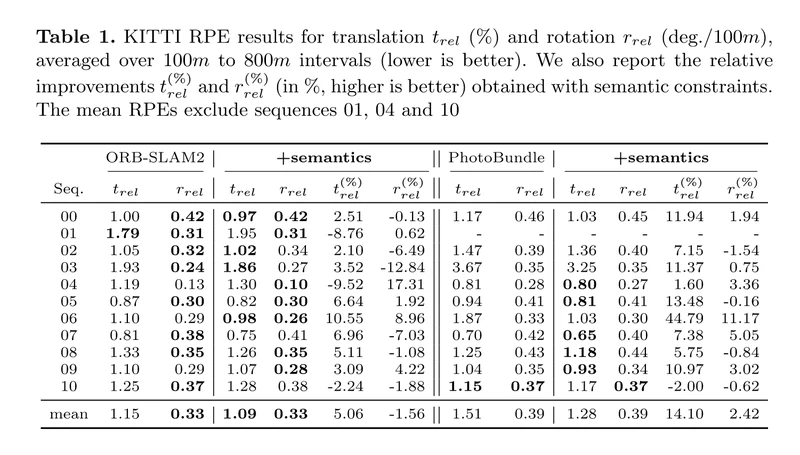
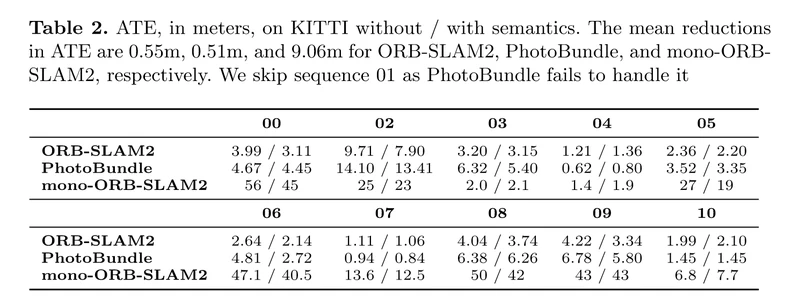
        该部分中，我们实验性地证明了整合语义中期约束到state-of-the-art的VO方法中，显著减少了平移漂移。
4.1. Experimental Setup
        对于segmentation，使用的是现成分类器(Multi-Scale Context Aggregation by Dilated Convolutions)在Cityscapes的预训练集。由于其在KITTI效果不是那么好，如图5。我们将不确定性用​和​来建模。分别代表了语义项的权重和分割的不确定性。

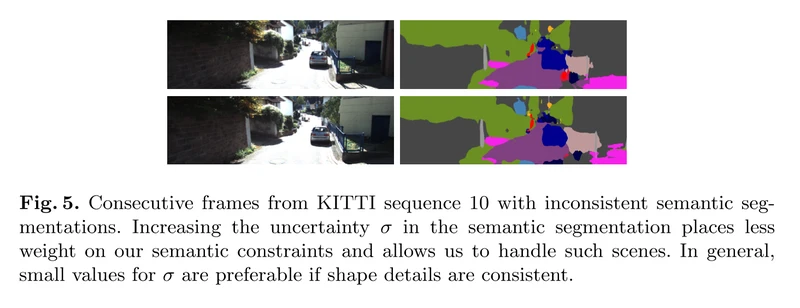
        基于每个数据集序列，我们经验性地挑选值。作者表示如上图所示的极端错误分类也能通过合理调整误差参数来让系统工作正常。
        对于P4B作者使用ground truth语义数据，展现了系统潜力的上限。
ORB-SLAM2 做间接法；PhotoBundle 做直接法。
        评价标准：
        RMSE: 均方根误差
        RPE: 相对姿态误差。测量估计量相对ground truth的固定长度间隔帧内的平均偏差。
        ATE: 绝对轨迹误差。测量两条轨迹之间点的绝对距离差。
        对于立体实验，文中测量 Relative RPE in % 来衡量漂移在语义约束引入后的相对减少。对于平移误差，相对RPE：$t_r$${}_e$${}_l^{(}$${}^{\%}$${}^{)}$定义为：

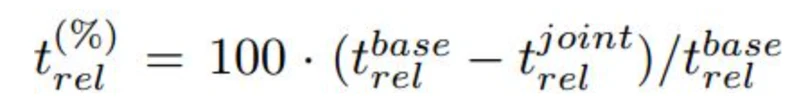
        其中$base$和$joint$分别是没有我们的约束和有我们的约束下的RPE值。(平移量的改善百分比)
4.2. Results

5. 感想

        整体理论并不是非常复杂，将语义当rgb图投影过来做匹配。而匹配过程生成了一个DT变换图。
        文章与另一篇《Long-term Visual Localization using Semantically Segmented Images》很像，区别在于：
        （1）它提出的模型是直接覆盖和原地点的点做比较，这个点的概率来自于建图的时候周围7*7的格子。
        （2）它使用粒子滤波而非优化方法。