欧拉图定义
经过图（无向图或有向图）中每条边一次且仅一次并且行遍图中每个顶点的回路(通路)，称为欧拉回路（欧拉通路）。存在欧拉回路的图，称为欧拉图。
欧拉图判断定理：
引理1：对于边数m > 0的连通图G, 如果G的每个顶点为偶数，则G有环
反证法：
假设G无环 => G是一个无向树 => G中至少包含两个树叶(度数为1的顶点) ，与每个顶点度数为偶数矛盾。
定理1：无向图G是欧拉图的充分必要条件是G 是连通图并且所有顶点度数为偶数。
证明：
平凡图显然成立(n = 1, m = 0)
（1）必要性 ： 设图G是欧拉图，证明G连通且且所有顶点度数为偶数。
G是欧拉图 => G中存在欧拉回路tour （根据欧拉图定义）
回路tour经过图G中每一个顶点 => G连通
对于回路tour上的任一中间顶点v，经过一条边e进入v，经过另一条边f离开v，进入v次数等于离开v次数 => 顶点v度数为偶数。
对于回路tour的起点和终点s，第一次离开，最后一次进入 => s度数为偶数。
充分性：G连通且所有顶点度数为偶数，证明G是欧拉图。（数学归纳法）
（a） 简单情况
n = 1, m = 0
n = 1, m = 1 (自环)
（b）归纳步骤（强归纳法）
设连通图G顶点数为N > 0 , 边数为M > 0。
假设任意顶点数 n < N, 边数m < M，且所有顶点度数为偶数的连通图Gi是欧拉图，证明顶点数 = N,
边数 = M且所有顶点度数为偶数的连通图G是欧拉图。
证明：欧拉图是若干边不相交的回路合并
findCircle(G)算法 //G是连通图, S是一个全局栈
1 根据引理1，G有环，找出一个回路C，将回路C压入栈S //PUSH(S, C)
2 删除回路C上的边, 得到G'= G - E[C]
3 如果G'连通，调用findCircle(G') //继续搜索G'中的回路
4 否则返回G' //算法终止时返回s个连通分量
mergeCircle(G) 算法
1 G' = findCircle(G) //调用findCircle(G), 得到回路集合S和非连通图G'
2 设G' = {G1, G2,...Gs}，其中s > 1
3 根据归纳假设，G'的每个连通分量Gi(1 <= i <= s)有一条欧拉子回路Ci
4 p = POP(S) //取出栈顶的回路p，p是findCircle算法找出的最后一条回路，删除p后，图G变成非连通图G'， 所以回路p与每一个连通分量Gi都有交点。
5 p依次与Gi(1 <= i <= s)的欧拉子回路Ci合并，得到C //此时C包含图G的所有顶点
6 while(S is not empty) //按搜索回路次序的逆序合并
7 p = POP(S)
8 C = p 合并 C //从回路p任一点出发，遇到和回路C的交点v时，先走完回路C回到交点v之后，继续走完p
mergeCircle(G)算法终止时，C包含图G的所有边和顶点，且边不重复，所以C是图G的一条欧拉回路，得证。
Fleury算法（避桥法）
从任意一点开始，沿着没有走过的边向前走
在每个顶点，优先选择剩下的非桥边，除非只有一条边
直到得到欧拉回路或者宣布失败
FLEURY(G)
u = v0; //如果求欧拉通路，则degree[v0]为奇数
while degree[u] > 0 {
FIND-BRIDGES(u) //从顶点u对子图G - {e1, e2, ..., ei-1}深搜，标记所有桥
//找出顶点u关联的一条非桥边或者桥边e
Edge e = null; //选择的边
for(Edge x = adj[u].first; x != null; x = x.next) {
v = x.v;//(u, v)
if(!visited[u][v]){//边(u, v)未访问
if(e == null){//第一条未访问的边e
e = x;
}
if(!isBrige(x) ){//x是非桥边
e = x;//
break;
}
}
}
//标记已访问的无向边e
visited[e.u][e.v] = true;
visited[e.v][e.u] = true;
degree[e.u]--;
degree[e.v]--;
P = P + {e} //将边e添加到欧拉回路或者欧拉通路
u = e.v
}
if(P.length() == M)
return P;//欧拉回路或者欧拉通路的边序列
else
Print("No euler circuit")
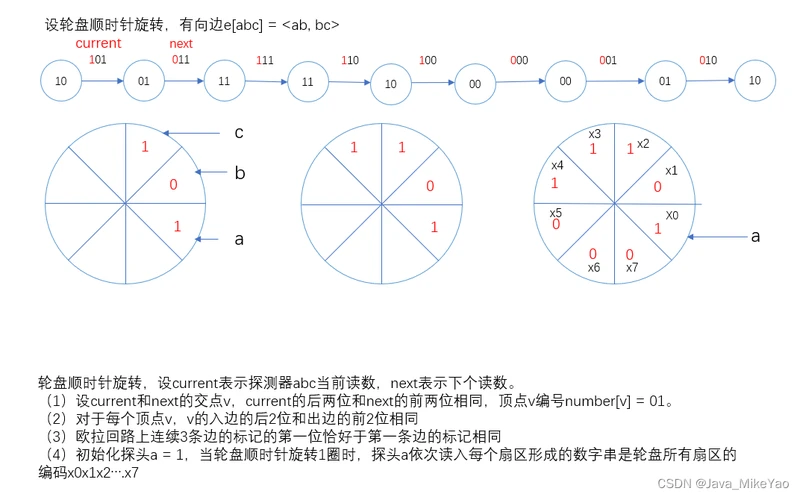
应用（轮盘设计）
设旋转磁鼓分成8个扇区，每个扇区标记一个0和1，有3个探测器能够读出连续的3个扇区的标记。现在的问题是：如何赋给扇区的标记，使得能够根据探测器读书确定磁鼓的问题。
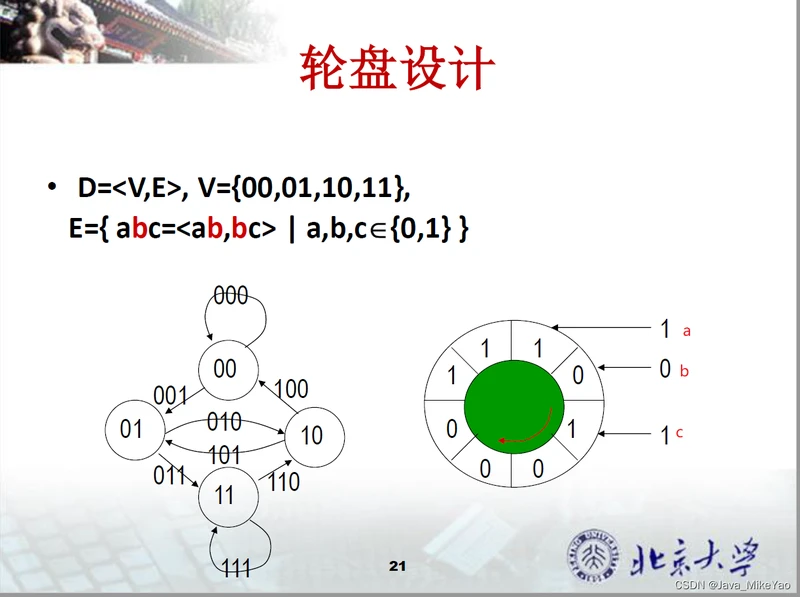
思路：
