复习
有限自动机分为两种:不确定的有限自动机(NFA)和确定的有限自动机(DFA)。我们分别用一个五元组表示。不确定的有限自动机:
- 有限状态集合S.
- 输入符号集合Σ
- 转换函数move:Sx(Σ∪(ε)->p(s))
- 状态S0是唯一的开始状态
- F包含于S是接受状态集合
确定的有限状态自动机1、2、4、5与NFA一样。转换函数move:Sx(Σ)->p(s),两者区别在于:有限自动机任何状态下没有ε转换,一个符号标记离开同一状态只有一条边。
MYT算法
规则如下:
1.st
不添加空串,添加一个状态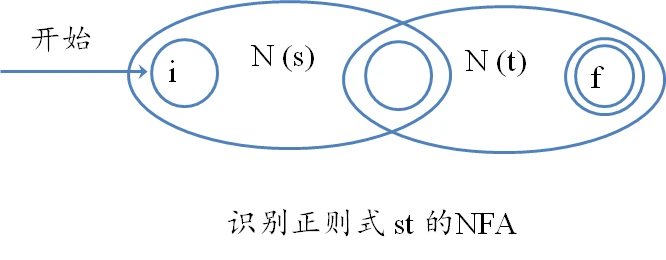
2.一个字符(可以是空字符)
添加一条边,一个状态
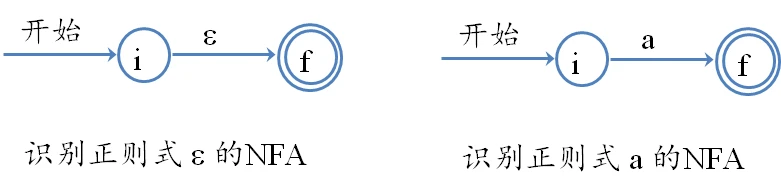
3.s|t
添加四个空串,四个状态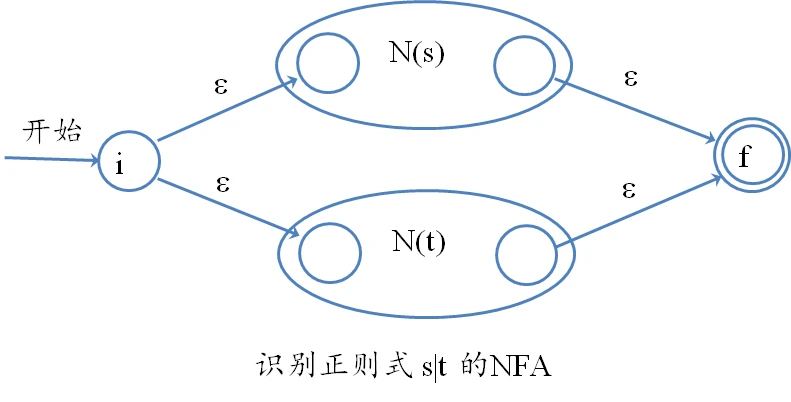
4.s*添加四个空串、四条边、四个状态(图下面一条i到f的边被遮住了)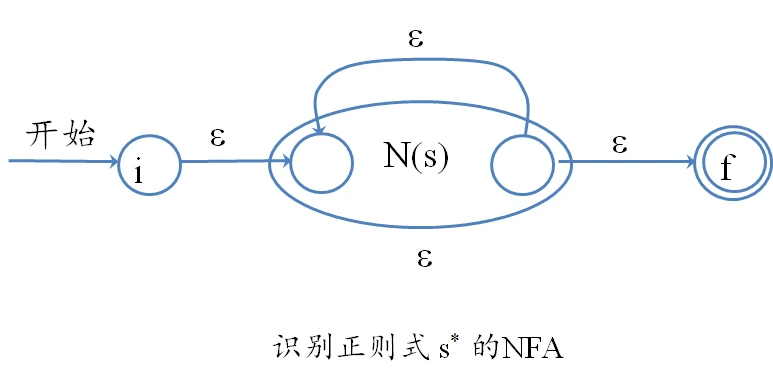
一些似乎不是很重要的性质:
- N(s)的状态数最多是s的状态数的两倍。
- N(s)的每一个状态有一个用Σ里的符号标记的指向其他节点的转换或者最多两个指向其他节点的ε转换。
MYT算法的分析
为了应付考试,我们可以说会手工建NFA就行。比较迅速的方法就是从嵌套多的地方入手,像搭积木一样搭建NFA。为了避免出错,建议时刻记住每个转换的添加的边数和空串数。
MYT算法的好处在于,任何字符串都能通过这个算法转换成NFA,它是沿着正则表达式的语法分析树自底向上递归处理的。不过我们可以发现,要添加的空串和边实在是太多了,这为我们后面继续转换成DFA带来了很多不少麻烦,因此这也是有代价的。
自顶向下算法
规则如下:

1.AB
添加一个状态
2.A|B
添加两条边,不添加空串和状态
3.A*
添加三条边、两个空串
自顶向下算法分析
和MYT算法同样,分块构建NFA。区别在于比较简单,引入空串、新边较少,之后化简就会容易。
