映射集合论

第一章集合及其运算

第二章映射

§1 函数的一般概念

§2 抽屉原理

§3 映射的一般性质

§4 映射的合成

§5 逆映射

§6 置换

§7 二元和n元运算

§8 集合的特征函数

§1 函数的一般概念

映射：

（1）设Ｘ和Ｙ是两个非空集合, 若根据某一法则f，使得"x $\in$ X，都存在唯一的y $\in$ Y与之对应，则称f为一个从Ｘ到Ｙ的映射。

（2）设X和Ｙ是两个非空集合。若Ｘ×Ｙ的子集f满足下列条件："x $\in$ X，都存在唯一的y $\in$ Y，使得(x,y) $\in$ f[或f(x)=y]，则称f是X到Ｙ的映射。

定义域—Ｘ称为f的定义域。x对应元素y称为x在f下的象(或值)，记为f(x)。而x称为y的原象。

值域—集合{f(x)|x $\in$ X}称为f的值域(或象集)，记为Im(f)。即{f(x)|x $\in$ X}=Im(f)⊆Y。

记法—“f是Ｘ到Ｙ的映射”常记为：f:X→Y。

映射关系图（略）

特殊映射：

1.限制与扩张：设f:Ｘ→Y，A⊆X，当把f的定义域限制在Ａ上时，就得到了一个j:A→Y，"x $\in$ A,j(x)=f(x),则称j为f在Ａ上的限制。反过来，f是j在Ｘ上的扩张。

2.部分映射：设f:A→Y ,A⊆X，则称f是X到Y（或Ｘ上）的一个部分映射。假定空集¢到Y有一个唯一映射（空映射），它也是Ｘ到Ｙ的部分映射。

3.映射的相等：设f,g:Ｘ→Y，则

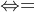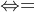
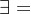f=g $\Leftrightarrow$ "x $\in$ X，有f(x)=g(x) f≠g $\Leftrightarrow$ $\exists$ x $\in$ X，使得f(x)≠g(x)

4.单射：设f:Ｘ→Y，若"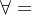 $\forall$ x1，x2 $\in$ X，只要x1≠x2，就有 f(x1)≠f(x2)。

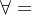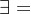5.满射：设f:Ｘ→Y，若" $\forall$ y $\in$ Y， $\exists$ x $\in$ X,使得f(x)=y。

6.双射：设f:Ｘ→Y，若f既是满射又是单射，则称f为双射，或一一对应。这时也称Ｘ与Ｙ对等，记Ｘ～Ｙ。

7.恒等映射：设 f:Ｘ→Ｘ，若"x $\in$ X，f(x)=x，则称f为Ｘ上的恒等映射。Ｘ上的恒等映射常记为Ix或I。

设f:Ｘ→Ｘ为集合X到集合X的一一对应，使得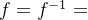 $f=f^{-1}$ ，则f是X到X的恒等映射（错）

重要结论：

定理1 f:A→B，设Ａ,B是有限集合。则

（1）若f是单射，则 |A|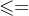 $\leqslant$ |B|；（2）若f是满射，则 |A| 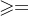$\geqslant$ |B|；（3）若f是双射，则 |A|=|B|。

定理2设f:A→B，Ａ,B是有限集合且|A|=|B|，则f是单射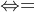 $\Leftrightarrow$ f是满射。

说明:(1)f是单射也是满射，从而f是双射；

(2)定理中Ａ,Ｂ为有限集合是必要条件，若Ａ,Ｂ不是有限集合，则结论不成立。

§2 抽屉原理

抽屉原理：n+1个物体放到n个抽屉里，则一定存在某一抽屉里面至少有两个物体。

抽屉原理强形式:设m1,m2,…,mn都是正整数,若把m1+m2+…+mn-n+1个物体放到n个抽屉里,则或第一个抽屉里至少有m1个物体,或第二个抽屉里至少有m2个物体,…,或第n个抽屉里至少有mn个物体。

说明:当m1=m2=…=mn=2时，m1+m2+…+mn-n+1=n+1。抽屉原理是强形式的一种特殊情况。

推论1：若有m个物体放到n个抽屉里，则一定存在某一个抽屉，它里面至少有[(m-1)/n]+1个物体。

推论2 若把n(m-1)+1个物体放进n个抽屉，则一定存在一个抽屉，里面至少有m个物体

此推论是强形式中，当m1=m2=…=mn=m 时的特殊情况。

推论3 若m1,m2,…,mn是n个正整数，且(m1+m2+…+mn)/n>r-1，则m1,m2,…,mn中至少有一个大于或等于r。

§3 映射的一般性质

象集（象）：设f:X→Y，A⊆X，由f和Ａ可以唯一的确定Ｙ中的一个子集，记为f(A)，f(A)={f(x)|x $\in$ A}。称f(A)为集合Ａ在f下的象集（象）。

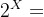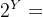说明：利用这种方法，由f可以确定一个从 2^X 到 2^Y 的映射，称为导出映射，仍记为f。则有

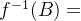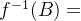原象：设f:X→Y，B⊆Y，则由f和Ｂ可以唯一确定X上的一个子集，记为 $f^{-1}(B)$ ，

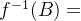$f^{-1}(B)$ ={x|f(x) $\in$ B，x $\in$ X} 称 $f^{-1}(B)$ 为在f下B的原象。 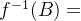$f^{-1}(B)$ 是X中在f下象落到B里的那些元素构成的集合。

性质：

定理1 设 f:X→Y ，C，D⊆Y，则

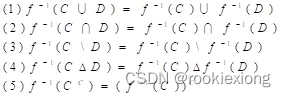
定理2 设 f:X→Y，A，B⊆X，则

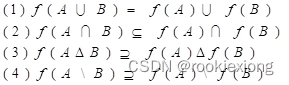
注意，两个集合的交（差、对称差）的象不一定与它们的象的交（差、对称差）相重合。

§4 映射的合成

映射合成的定义：设f:A→B，g:B→C。若存在一个从A到C的映射记为h，并且"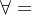 $\forall$ x $\in$ A，h(x)=g(f(x))，则称h为映射f与g的合成。h记为gºf(gf)，即h=gºf=gf

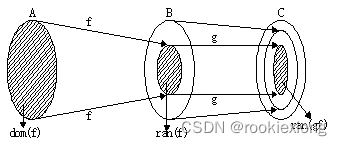
性质：虽然交换律不成立，但却有结合律成立。

定理1 设f:X→Y，g:Y→Z，h:Z→W，则 h(gf)=(hg)f

定理2 设f:X→Y,则fºIX=IYºf=f

定理3 设f:X→Y,g:Y→Z，则

（1）若f与g都是单射，则gf也是单射；

（2）若f与g都是满射，则gf也是满射；

（3）若f与g都是双射，则gf也是双射。

定理4 设f:X→Y，g:Y→Z，则

（1）若gf是单射，则f是单射；

（2）若gf是满射，则g是满射；

（3）若gf是双射，则f是单射，g是满射。

说明：gf是单射时，f是单射，但g不一定是单射；gf是满射时，g是满射，但f不一定是满射。

§5 逆映射

逆映射的定义：设f:X→Y。若存在一个映射g:Y→X,使得gf=IX且fg=IY，则称映射f是可逆的，而g称为f的逆映射。由定义，f可逆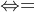 $\Leftrightarrow$ gf=IX与fg=IY同时成立，缺一不可。

左逆与右逆映射：设f:X→Y，则

(1)若存在一个映射g:Y→X,使得gf=IX，则称f是左可逆的，g称为f的左逆映射。

(2)若存在一个映射h:Y→X,使得fh=IY，则称f是右可逆的，而h称为f的右逆映射。

逆映射的性质：

定理1 设f:X→Y，则f是可逆的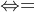 $\Leftrightarrow$ f为双射。

定理2 设f:X→Y，则若f是可逆的，那么f的逆映射是唯一的。f逆记为f-1。

定理3 设f:X→Y，g:Y→Z，若f和g都是可逆的，则gf也是可逆的且(gf)-1=f-1g-1，（f–1)-1=f。公式(gf)-1=f–1g-1称为“穿脱原则”，脱的次序正好与穿的次序相反。

定理4 设f:A→B，A≠ $\o$ ¢，则

（1）f是左可逆的，当且仅当f是单射；

（2）f是右可逆的，当且仅当f是满射；

（3）f既是左可逆的又是右可逆的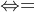 $\Leftrightarrow$ f是双射；

（4）若f是双射，则f的左逆映射等于右逆映射。

§6 置换

置换的定义：有限集合S到自身的一一对应称为S上的一个置换。若|S|=n，则S上的置换称为n次置换。S上的n次置换个数等于n!。

n阶有限群同构于n阶置换群;

n阶置换群之间的代数运算就是置换的乘法运算。

置换的表示：用1，2，…，n表示n元集S的各元素。

设S={1,2,…,n}，s是S上置换，即s:S→S, s是一一对应。

"i $\in$ S ，存在唯一ki $\in$ S对应，即s(i)=ki。由于S只有n个元素，所以可把S的n个元素写在一行上，而把每个元素在s下的象ki写在这个元素的下面，就得到如下的一个表:

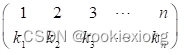
说明：一个n次置换就是S中的元素的一个全排列。

置换的乘积（合成）

乘积的表示方法：a与b的乘积（合成）就可记为ab，并且"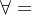 $\forall$ i $\in$ S (i)ab=((i)a)b ，或简记为(i)ab。

几种特殊的置换：

1. S上的恒等置换记为I，即

2. 置换的逆置换：

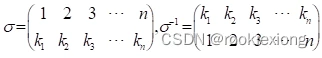
s·s-1=s-1·s=I

即s的逆s-1就是s的表示式的上下两行交换后所得到的表达式。

3.循环置换、对换

定义1 设s是S上的一个n次置换，若i1s=i2,i2s=i3,

…,ik-1s=ik,iks=i1,而"i $\in$ S\{i1,i2,…,ik},is=i，则称s是一个k—循环置换，记为(i1i2…ik)。即

(i1i2…ik)=(i2i3…iki1)=(i3i4…iki1i2)=…=(iki1i2…ik-1)

当k＝2时，2－循环置换也称为对换,简记为(i,j)。如图：

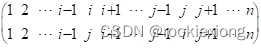
4. 循环置换的逆、对换的逆

循环置换的逆为:

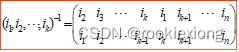
对换的逆就是其本身。

循环置换的性质：

映射的合成运算不满足交换律，故置换的乘积也不满足交换律。即"a,bÎSn ，ab¹ba。但对于两个没有共同数字的循环置换却是可交换的。

定义1 设(i1i2 …ik)与(j1j2…jr)是两个循环置换，若(i1i2…ik)∩(j1j2…jr)= $\o$ ¢，则称这两个循环置换是没有共同数字的循环置换（或称不相交）。

定义2 若一个置换能被分解为偶数个对换的乘积，则称这个置换为偶置换。若一个置换能被分解奇数个对换的乘积，则称这个置换为奇置换。

1个奇置换×1个偶置换＝奇置换；1个奇置换×1个奇置换＝偶置换；

任意偶数个奇置换乘积是偶置换；

任意奇数个偶置换乘积是偶置换；任意奇数个奇置换乘积是奇置换。

定理1 设a=(i1i2 …ik)与b=(j1j2 …jr)是两个没有共同数字的循环置换，则a与b是可交换的，即ab=ba。

定理2 结合律成立。

定理3（置换的循环分解）每个置换都能分解成若干个没有共同数字的循环置换的乘积。

若不计这些循环置换的顺序，则这种分解是唯一的。

定理4 每个循环置换可被分解成若干个对换的乘积。

定理5 每个置换能被分解成若干个对换的乘积。

定理6 若把置换分解成若干个对换的乘积，则对换的个数的奇偶性是不变的。

§7 二元和n元运算

定义1 设X,Y,Z为三个非空集合，j:X×Y→Z。则称j为X与Y到Z的一个二元运算。

当X=Y=Z时，即j:X×X→X，则称j为X上的二元(代数)运算。

定义2 设X,Y是两个非空集合，j:X→Y。称j为X到Y的一个一元运算。

当X=Y,即若j:X→X，则称j为X上的一元运算。也称j为X的一个变换。

定义3 设X1,X2,…,Xn,Y为非空集合，

j:X1×X2×…×Xn →Y。则称j为X1,X2,…,Xn到Y的一个n元运算。

若X1=X2=…=Xn=Y=X，即j:X×X×…×X→X，则称j为X上的n元运算。

§8 集合的特征函数

定义1 设X是一个集合，E⊆X，jE:X→{0,1}。" $\forall$ x $\in$ X，

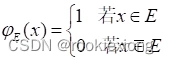
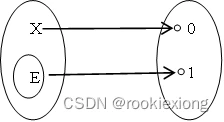
则称j为子集E的特征函数。

说明：

1.如图所示表示了这个映射的特征。

2.特征函数是由E唯一确定的，反过来，对任一特征函数都能唯一地确定一个E。因此，集合E与它的特征函数是一一对应。

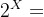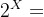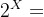3.子集E与它的特征函数jE一一对应，而X共有| 2^X |个子集，若用Ch(X)={jE|jE:X→{0,1},E⊆X}表示时，则Ch(X)也应该有| 2^X |个，即 2^X ~Ch(X)。

4.集合的特征函数是描述集合的另一种方法。

映射 集合论

§1 函数的一般概念

§2 抽屉原理

§3 映射的一般性质

§4 映射的合成

§5 逆映射

§6 置 换

§7 二元和n元运算

§8 集合的特征函数

知秋君

相关推荐

§6 置换