给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1
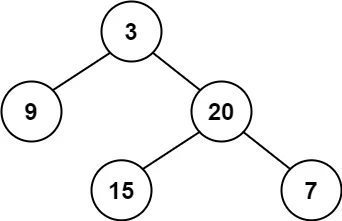
输入:root = [3,9,20,null,null,15,7]
输出:true
思路一: 对每一个节点进行递归处理
如何计算二叉树中任意一个节点的高度?
h
e
i
g
h
t
=
m
a
x
(
h
e
i
g
h
t
(
p
.
l
e
f
t
)
,
h
e
i
g
h
t
(
p
.
r
i
g
h
t
)
)
+
1
;
p
是
非
空
节
点
height=max(height(p.left), height(p.right)) +1;p是非空节点
height=max(height(p.left),height(p.right))+1;p是非空节点
h
e
i
g
h
t
=
0
;
p
是
非
空
节
点
height=0;p是非空节点
height=0;p是非空节点
递归的计算每一个节点
- 遍历到当前节点,并计算左右子树的高度,如果高度差大于1,返回false
- 递归的遍历左子树与右子树
class Solution {
private:
int depthTree(TreeNode* root){
if(root == NULL) {
return 0;
}
return max(depthTree(root->left), depthTree(root->right)) + 1;
}
public:
bool isBalanced(TreeNode* root) {
if(root == NULL){
return true;
}
return abs(depthTree(root->left) - depthTree(root->right)) <= 1
&& isBalanced(root->left)
&& isBalanced(root->right);
}
};
思路二: 从底往上对每一个节点进行递归
感受一下“后序遍历”
- 对于当前遍历到的节点,先递归的判断其左右子树是否平衡
- 再判断当前节点是否平衡
class Solution {
private:
int depthTree(TreeNode* root) {
if(root == NULL){
return 0;
}
int left = depthTree(root->left);
int right = depthTree(root->right);
if(left == -1 || right == -1 || abs(left - right) > 1) {
return -1;
}else {
return max(left, right) + 1;
}
}
public:
bool isBalanced(TreeNode* root) {
return depthTree(root) >= 0;
}
};
