单循环比赛公式推导过程

这是一个算法作业，老师说要用分治思想解决，在网上找了都讲解的不是很明白，比赛对数为奇数时，有点费解。不过最后还是想明白了，顺便把作业放这，有兴趣了解的可以看一下，逃）

问题：

有N个运动员进行单循环赛，即每个运动员要和所有其他运动员进行一次比赛。
1．试用分治法为N个运动员安排比赛日程。
2．要求每个（或队）运动员每天只能进行一场比赛，且当运动员人数(队数)为偶数时，整个比赛在N-1天内结束，为奇数时，在N天内结束；
3．将运动员从1到N编号。

思路：
我们用表格的方式来表示循环赛的日程安排，最左边的一列表示队号，每一行表示相应队比赛每天的对手，即a[i][j]表示第i队第j天的对手。
我们从两个队的比赛开始，并发现其中规律：

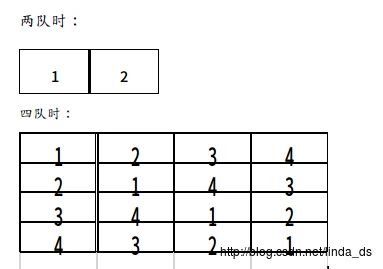
其中，四队的表格可以从两队的表格产生的：

但这只能解决2的幂的队数的循环赛日程。

为了解决更普遍的队数，我们考虑队数为偶数时，它必然可以被2整除，商为偶数或奇数。商为偶数可以用上面的方法得到结果，商为奇数时，就不行了。
我们先来看一个例子，队数为6时，它的一半为3，是奇数，不能用上面的方法，我们先考虑它的子问题：队数为4时，就是上面求出的结果了，我们要从队数4产生6的结果：

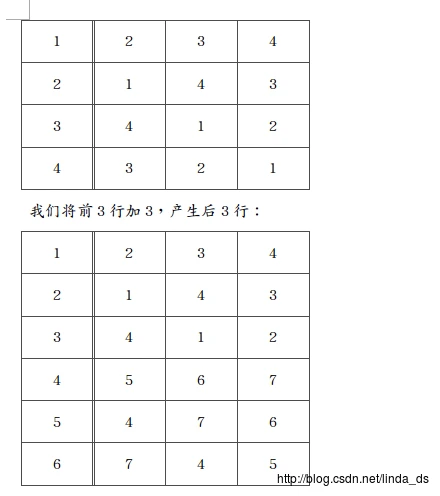
我们可以看到后3行其实和前3行是一样的，只是编号变了而已。为了让编号在6以内，我们要改变编号7的对应情况，可以看出编号7是由编号4产生的，所以我们只要让它们相对的队组成一队就可以了，即3-6,2-5,1-4。

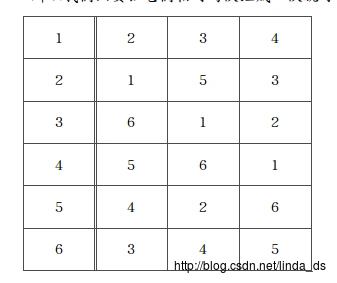
至此，我们只解决了6队的一部分情况，第5、6列还没有产生：
由上面可知，第1行还缺5,6，第2行缺4,6，第3行缺4,5，那么它们该怎么排列才不会冲突呢？我们看到1,2,3行的5,6列在4,5,6中取两个值，可以用循环队列的形式解决，如下：

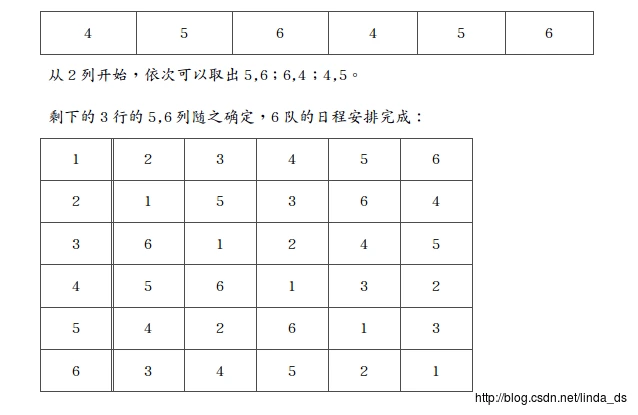
到此，我们来想更普遍的情况，任意一个队数n，是否都可以分解为上面的两种情况？
首先，我们看任意n是否能终止分解？如下伪代码：

 while i != 1 do
    if i % 2 == 0
        i  i/2
    else  i  i+1

对于任何大于2的数除以2再加1或者加1再除以2，它的规模都会缩小，所以这最终是可以终止的。接着我们看是否能分解为上面两种情况：
n为奇数时，用n+1代替计算，即转化为偶数的队数。
n为偶数时，分两种情况，（1）n/2为偶数，（2）n/2为奇数。（1）继续被2除，直到商为1，即转化为第一种情况，n是2的幂，或者商为大于1的奇数（2），转化为（2）。（2）就是第二种情况。所以，任意n是可以分解为上面两种情况的，而且是可以终止的。
把上述的内容一般化，即为我们解决该问题的解：
1．tournament(a[][],n)用递归把问题分解为多个子问题，其中odd(n)判断n是否为奇数,makecopy(a[][], n)用上面的两种情况中的一种产生日程：

tournament(a[][], n)
if n == 1
    a[0][0] = 1;
    return;
if odd(n)
        tournament(a[][], n+1);
else
        tournament(a[][], n/2);
makecopy(a[][], n);
return;

2．odd(n)判断n是否为奇数：

odd(n)
return n&1;

3．makecopy(a[][], n)用上面的两种情况中的一种产生日程，如果n/2为偶数用第一种，即copy(a[][], n)，n/2为奇数用第二种，即copyodd(a[][], n):

makecopy(a[][], n)
m = n/2;
if odd(m)
        copyodd(a[][], n);
else 
        copy(a[][], n);

4．copy(a[][], n)第一种情况的日程产生方法，为了更好的理解，我们从1*1到2*2到4*4的表格产生情况开始（假设表为二维数组a）：

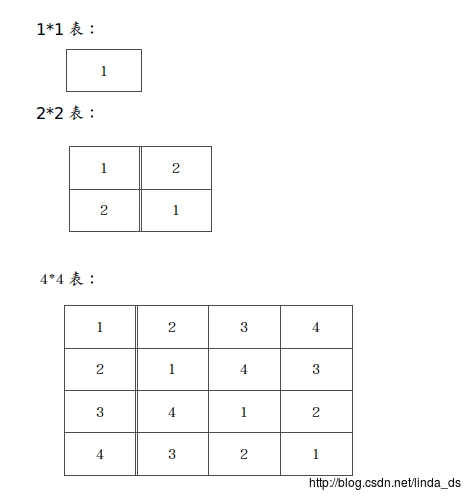
1*1表产生2*2表是将a[0][0]加1放到a[0][1],再将这个值复制到a[1][0],将a[0][0]中的数复制到a[1][1].
同理，2*2表产生4*4表是将2*2表相应位置(即4*4表左上角)加2放到右上角，再复制到左下角，将左上角复制到右下角：

copy(a[][], n)
m = n/2;
for i 0 to m-1 do
        for j 0 to m-1 do
            a[i][j+m] = a[i][j]+m;
            a[i+m][j] = a[i][j+m];
            a[i+m][j+m] = a[i][j];

5．copyodd(a[][], n)为第二种情况的日程产生方法，上面我们已经了解了队数为6时的产生情况，我们把情况一般化，队数为n，且m=n/2为奇数，且队数为m+1的子情况已经解决：

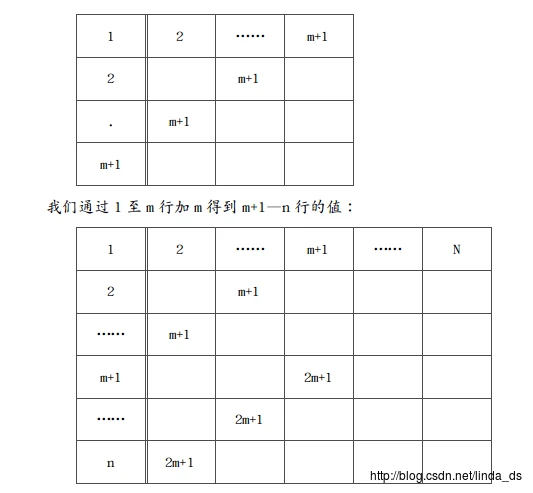
因为2m+1已经超出n的范围，所以我们将值为m+1和2m+1的队组成一组，即1—m+1,2—m+2,3—m+3,……,m—n.
因为它们之间都相差m，所以可以用一个数组b的索引和值的对应关系来表示：

至此，我们完成了部分对应关系，接着要解决m+2到n列的对应关系：
第1行还缺m+2……n;
第2行缺 m+3……n, m+1;
第3行缺 m+4……n, m+1,m+2;
……
第m行缺 m+1……n-1.
可以看出它们是在m+1到n之间循环取值，且每次取m-1个。所以，可以用一个包括2个m+1到n连续排列的数组表示：
0 1 …… m-1 m m+1 …… n-1
m+1 m+2 …… n m+1 m+2 …… n
剩下未分配的随之解决。

copyodd(a[][], n)
m = n/2;
for i0 to n-1 do
        b[i] = m+i+1;
for i0 to m-1 do
        for j  0 to m-1 do
        if a[i][j]> m 
            a[i][j] = b[i];
            a[i+m][j] = i+1;
        else
            a[i+m][j] = a[i][j] + m;
        for j 1 to m-1
            a[i][m+j] = b[i+j];
            a[b[i+j]][m+j] = i+1;

循环赛算法到此完成。
数据结构：
一个二维数组a[n][n]存储日程表，一个一维数组b[n]存储映射关系。
效率分析：
T(n) = T(n/2)+f(n)
其中，f(n)为copy()的时间
f(n) = (n/2)^2
推出：T(n) = T(n/2)+(n/2)^2
因为二分可以分log n次，所以T(n) = (n/2)^2+(n/4)^2+…+1 ;
所以，T(n)∈O(n^2)。
参考资料：
http://www.cppblog.com/cdy20/archive/2009/04/01/78573.html?yyue=a21bo.50862.201879#_Toc225487252

http://www.cnblogs.com/hoojjack/p/4211941.html

http://www.cnblogs.com/kelin1314/archive/2009/07/15/1523905.html

知秋君

相关推荐