k近邻算法的应用实例

基础知识

实验环境

实验数据

实验步骤及代码

（1）导入本次实验所需的包及数据

（2）读入数据后，我们可以画出一些特征来观察数据的分布规律

（3）刻画我们的距离函数

（4）定义K近邻分类算法

（5）定义测试KNN分类效果的函数

（6）寻找分类效果最优的K值

算法对比

结论

基础知识

K-Nearest Neighbor 简介

K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一，属于一种懒惰学习算法。该方法的思路是：在特征空间中，如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别，则该样本也属于这个类别。

用我自己的理解来说，KNN本质的思想就是“物以类聚，人以群分”，即古人所谓的“观其友，识其人”。如果你想知道一个人的品行（Label）怎么样，只要了解他身边朋友的品行即可。如下图所示，这就是典型的一个KNN分类场景。

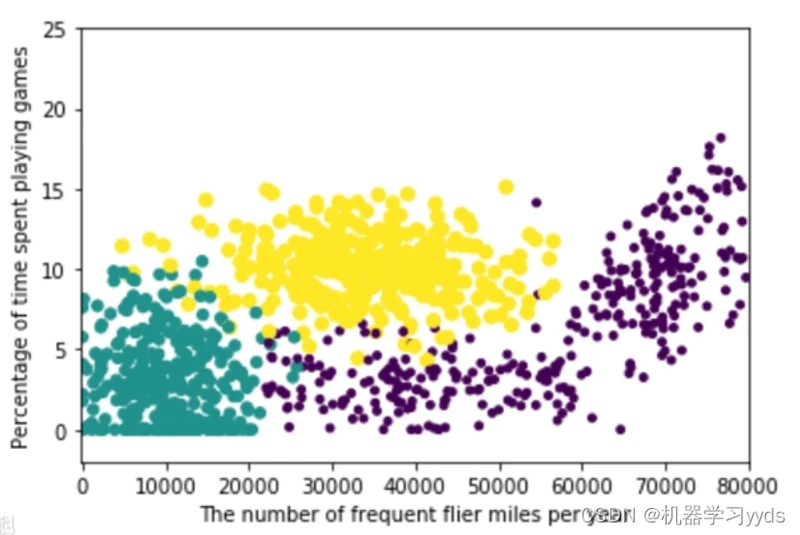
图 K近邻分类

K-Nearest Neighbor 算法

KNN的算法流程也很简单，可以理解为每次新进入一个数据点，我们就以距离函数对它进行一次公投，离它最近的K个点的标签中，出现最多次数的标签即为新数据点的标签.
因此根据上述，影响KNN算法的两个最重要因素就是距离度量方式以及K值的选择：

距离度量一般采用欧氏距离，在度量之前，应该将每个属性的值规范化，这样有助于防止具有较大初始值域的属性比具有较小初始值域的属性的权重过大。

K 值的选择会对算法的结果产生重大影响。K值较小意味着只有与输入实例较近的训练实例才会对预测结果起作用，但容易发生过拟合；如果 K 值较大，优点是可以减少学习的估计误差，但缺点是学习的近似误差增大，这时与输入实例较远的训练实例也会对预测起作用，使预测发生错误。

实验环境

硬件：PC机一台，Windows 8 及以上；
软件：VS Code 、Python 3 及以上.

实验数据

鸢尾花数据集 Fisheriris_data

实验步骤及代码

（1）导入本次实验所需的包及数据

代码：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split

data = pd.read_excel('fisheriris_data.xlsx', header = None, names=['Feature1', 'Feature2', 'Feature3'])
label = pd.read_excel('fisheriris_label.xlsx', header = None, names=['label'])
X = data[['Feature1', 'Feature2', 'Feature3']].values
Y = label['label'].values
X = np.array(X)
Y = np.array(Y)
data.head()

因为我们的数据集大小是 150 X 3 ，所以我们在读入数据的时候自定义数据的第一列为Feature1，第二列为Feature2，第三列为Feature3.

我们每次读取完数据，都可以利用Pandas中的head函数查看数据的前五行，以检查读入正确性.

结果：

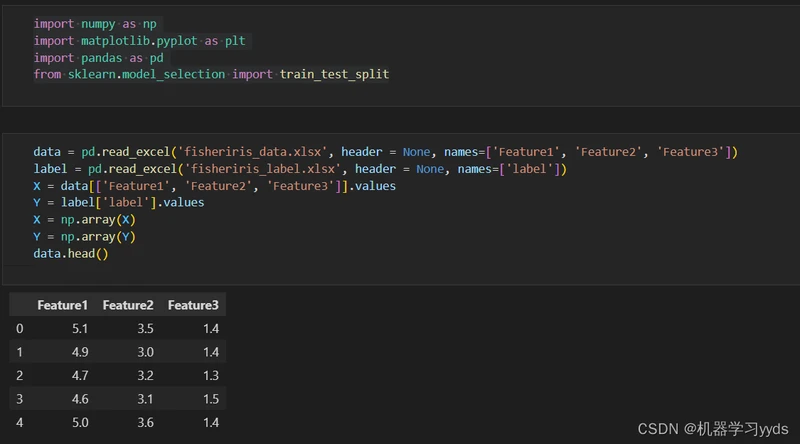
数据读入完成！

注意：因为我们本次使用的数据量很小，且数据数值不大，所以无需对其进行归一化处理。但是如果读者们在处理一些大数据任务时，要记得先对数据进行清洗与预处理。

（2）读入数据后，我们可以画出一些特征来观察数据的分布规律

代码：

def showdatas(data, label):
    fig, axs = plt.subplots(nrows=2, ncols=2, sharex=False, sharey=False, figsize=(13,8))
    numberoflabel = len(label)
    labelscolor = []    #设置标签的颜色以区分标签
    for i in label:
        if i == "'setosa'":
            labelscolor.append('black')
        if i == "'versicolor'":
            labelscolor.append('orange')
        if i == "'virginica'":
            labelscolor.append('red')
    #画出数据分布的散点图，以Feature1，Feature2数据画散点图,散点大小为15，透明度0.5
    axs[0][0].scatter(x=data[:, 0], y=data[:, 1], color=labelscolor, s=15, alpha=.5)
    axs0_title_text = axs[0][0].set_title(u'Feature Classifition')
    axs0_xlabel_text = axs[0][0].set_xlabel(u'Feature1')
    axs0_ylabel_text = axs[0][0].set_ylabel(u'Feature2')
    plt.setp(axs0_title_text, size=9, weight='bold', color='red')
    plt.setp(axs0_xlabel_text, size=7, weight='bold', color='black')
    plt.setp(axs0_ylabel_text, size=7, weight='bold', color='black')
    
    # 画出散点图,以Feature1，Feature3数据画散点图,散点大小为15,透明度为0.5
    axs[0][1].scatter(x=data[:, 0], y=data[:, 2], color=labelscolor, s=15, alpha=.5)
    axs1_title_text = axs[0][1].set_title(u'Feature Classifition')
    axs1_xlabel_text = axs[0][1].set_xlabel(u'Feature1')
    axs1_ylabel_text = axs[0][1].set_ylabel(u'Feature3')
    plt.setp(axs1_title_text, size=9, weight='bold', color='red')
    plt.setp(axs1_xlabel_text, size=7, weight='bold', color='black')
    plt.setp(axs1_ylabel_text, size=7, weight='bold', color='black')
    
    # 画出散点图,以Feature2，Feature3数据画散点图,散点大小为15,透明度为0.5
    axs[1][0].scatter(x=data[:, 1], y=data[:, 2], color=labelscolor, s=15, alpha=.5)
    axs2_title_text = axs[1][0].set_title(u'Feature Classifition')
    axs2_xlabel_text = axs[1][0].set_xlabel(u'Feature2')
    axs2_ylabel_text = axs[1][0].set_ylabel(u'Feature3')
    plt.setp(axs2_title_text, size=9, weight='bold', color='red')
    plt.setp(axs2_xlabel_text, size=7, weight='bold', color='black')
    plt.setp(axs2_ylabel_text, size=7, weight='bold', color='black')
    
    # 设置图例
    label1 = plt.Line2D([], [], color='black', marker='.',
                              markersize=6, label='setosa')
    label2 = plt.Line2D([], [], color='orange', marker='.',
                               markersize=6, label='versicolor')
    label3 = plt.Line2D([], [], color='red', marker='.',
                               markersize=6, label='virginica')
    # 添加图例
    axs[0][0].legend(handles=[label1, label2, label3])
    axs[0][1].legend(handles=[label1, label2, label3])
    axs[1][0].legend(handles=[label1, label2, label3])
    # 显示图片
    plt.show()
    
showdatas(X,Y)

结果：

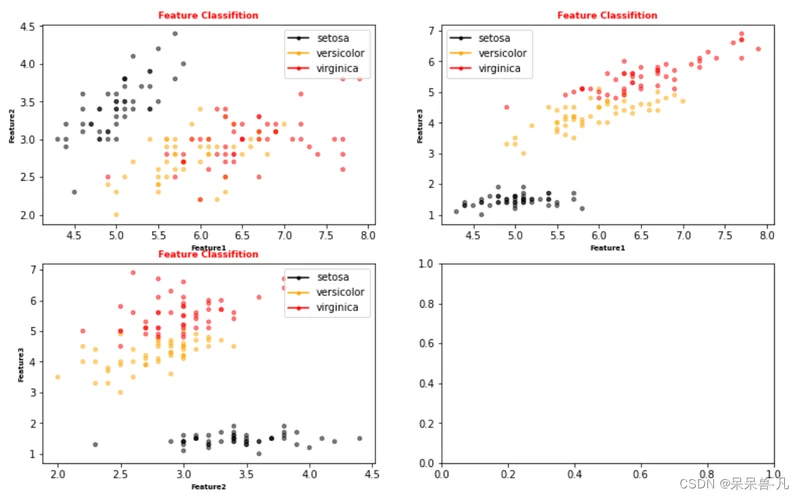
图鸢尾花数据的分布规律

从图中，我们可以看出，数据中的Feature2与Feature3对数据分布的影响较大，数据分类明显。

（3）刻画我们的距离函数

这里我只使用了两种距离，分别是

曼哈顿距离

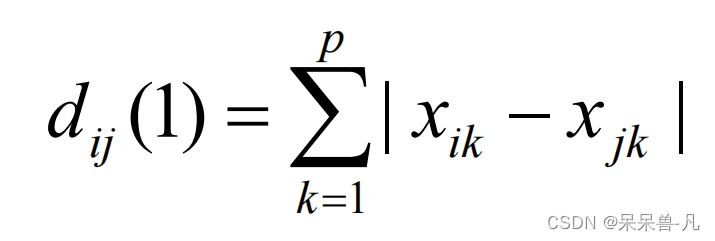
欧氏距离

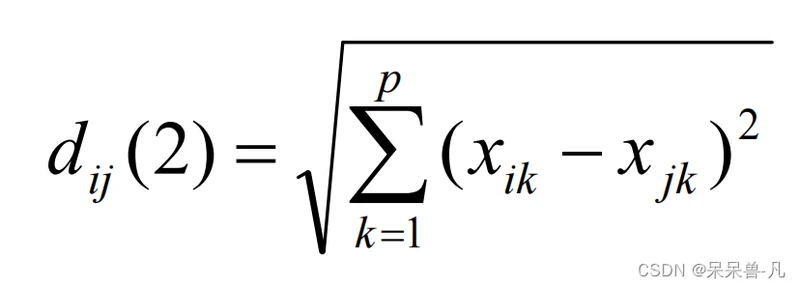
代码：

def ManhattanDis(testdata, traindata):  #曼哈顿距离
    datasize = traindata.shape[0]
    diff = np.tile(testdata, (datasize,1)) - traindata  #计算每个点的间距
    dist = np.sum(abs(diff), axis=1)    #绝对值相加
    return dist
    
def EuclideanDis(testdata, traindata):  #欧氏距离
    datasize = traindata.shape[0]
    diff = np.tile(testdata, (datasize,1)) - traindata
    dist = (np.sum(diff ** 2, axis=1)) ** 0.5   #平方开根号
    return dist

就是对着数学公式敲hhh

（4）定义K近邻分类算法

代码：

#定义K近邻分类
def Knn_Classify(testdata, traindata, label, k):
    dist = EuclideanDis(testdata, traindata)    #这里选取欧式距离
    #排序,返回下标
    sortDistindix = np.argsort(dist)
    
    Classcount = {}
    for i in range(k):  #对选取的k个样本所属的类别进行统计
        voteLabel = label[sortDistindix[i]] #每次找到最近的标签
        Classcount[voteLabel] = Classcount.get(voteLabel, 0) + 1    #记录
    maxCount = 0
    for key, value in Classcount.items():
        if value > maxCount:
            maxCount = value
            classes = key
    return classes

依据写在文章最开头的思想，定义K近邻分类器，根据最近的K值赋标签。

测试结果：

（5）定义测试KNN分类效果的函数

为了方便我们对于KNN分类效果的测试以及选取最优K值，我们定义该函数用以测试KNN效果

代码：

#用于测试
def KNN_test(X, Y, splitRatio, k):
    nums = int(X.shape[0] * splitRatio) #代表测试集的长度
    train_x, test_x, train_y, test_y = train_test_split(X,Y,test_size=splitRatio)
    ErrorRate = 0   #错误样例
    for i in range(nums):
        Result_Classify = Knn_Classify(test_x[i], train_x, train_y, k)
        print("分类结果:%s\t真实类别:%s" % (Result_Classify, test_y[i]))
        if Result_Classify != test_y[i]:
            ErrorRate += 1
    print("错误率:%f%%" % (ErrorRate / float(nums) * 100))
    return ErrorRate / float(nums) 
R = KNN_test(X, Y, 0.5, 3)

我们使用了50%的数据为训练集，50%的数据为测试集

结果：

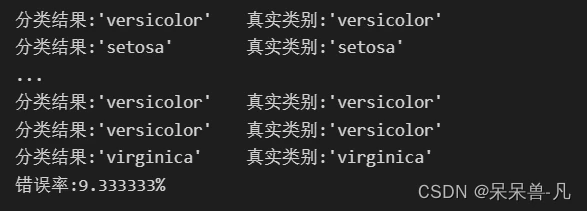
可以看到，我们的KNN分类器效果还可以，能达到90%以上的准确度。

（6）寻找分类效果最优的K值

代码：

#K取值[1,10]进行检验，找出分类效果最好的K
ERROR = []
for q in range(1,11):
    R = KNN_test(X, Y, 0.5, q)
    ERROR.append(R)
plt.title('KNN Error',fontsize = 14)
plt.xlabel('K',fontsize = 14)
plt.ylabel('Error',fontsize = 14)
plt.plot(ERROR, '-p', color='grey',
        marker = 'o',
        markersize=8, linewidth=2,
        markerfacecolor='red',
        markeredgecolor='grey',
        markeredgewidth=2)
plt.show()

结果：

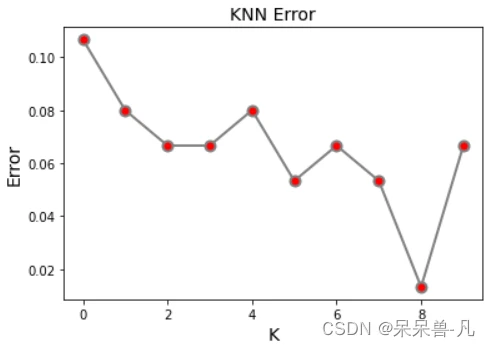
从上图中，我们可以看出，当K=8的时候，该KNN分类器的误差最小，但是简单的一次实验具有随机性，如果大家想要得到更精确的数据，可以多做几次实验，观察一下K的分布规律，找出最优的K值。

到此，一个简单的K近邻分类算法实验就算基本完成了，至于后续的优化，感兴趣的读者可以自己去继续研究。

算法对比

我们还可以基于Python中的scikit-learn包，利用其中自带的Libsvm，使用SVM进行分类，并与KNN进行对比。

代码：

#利用Python自带的Libsvm包进行测试
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV
train_x, test_x, train_y, test_y = train_test_split(X,Y,test_size=0.5)
# rbf核函数，设置数据权重
svc = SVC(kernel='rbf', class_weight='balanced',)
c_range = np.logspace(-5, 15, 11, base=2)
gamma_range = np.logspace(-9, 3, 13, base=2)
# 网格搜索交叉验证的参数范围，cv=3,3折交叉，n_jobs=-1，多核计算
param_grid = [{'kernel': ['rbf'], 'C': c_range, 'gamma': gamma_range}]
grid = GridSearchCV(svc, param_grid, cv=3, n_jobs=-1)
# 训练模型
clf = grid.fit(train_x, train_y)
# 计算测试集精度
score = grid.score(test_x, test_y)
print('精度为:%s' % score)

结果：

精度为0.96

可以看出，利用Python自带的SVM分类器，能够做到比KNN略胜一筹的分类效果，但是由于我们使用的数据集量太小，所以结论并不具有显著意义，还需要在更多的数据集上测试。

KNN与SVM的对比：

KNN 基本原理;就是找到训练数据集里面离需要预测的样本点距离最近的 k 个值（距离可以使用比如欧式距离，k 的值需要自己调参），然后把这 k 个点的 label 做个投票，选出一个 label 做为预测。对于 KNN，没有训练过程。只是将训练数据与测试数据进行距离度量来实现分类；
SVM 则需要超平面 wx+b 来分割数据集（此处以线性可分为例），因此会有一个模型训练过程来找到 w 和 b 的值。训练完成之后就可以拿去预测了，根据函数 y=wx+b 的值来确定样本点 x 的 label，不需要再考虑训练集。对于 SVM，是先在训练集上训练一个模型，然后用这个模型直接对测试集进行分类。

结论

K最近邻(k-Nearest Neighbor，KNN)的主要优点：

算法简单直观，易于应用于回归及多分类任务；

基础知识

实验环境

实验数据

实验步骤及代码

（1）导入本次实验所需的包及数据

（2）读入数据后，我们可以画出一些特征来观察数据的分布规律

（3）刻画我们的距离函数

（4）定义K近邻分类算法

（5） 定义测试KNN分类效果的函数

（6）寻找分类效果最优的K值

算法对比

结论

知秋君

相关推荐

（5）定义测试KNN分类效果的函数