紧接上一篇:http://blog.csdn.net/yinhun2012/article/details/79391444
这篇我们推导三角函数中加减法与和差化积公式。
1.加减法公式,加减法公式主要针对“普通”角变“特殊”角,这个意义就在于,我们知道一些特殊角度的值,比如:
sin30° = 1/2,sin60° = √3/2 ,sin45° = √2/2
那么sin75° = sin(45°+30°) = sin45°+sin30°?
亦或者sin15° = sin(45°-30°) = sin45° - sin30°?
这里到底能不能直接用加减法去做运算呢,我们来通过绘画的方式展现到底sin75°或者说sin(α+β)度和sinα与sinβ的关系,如下图:
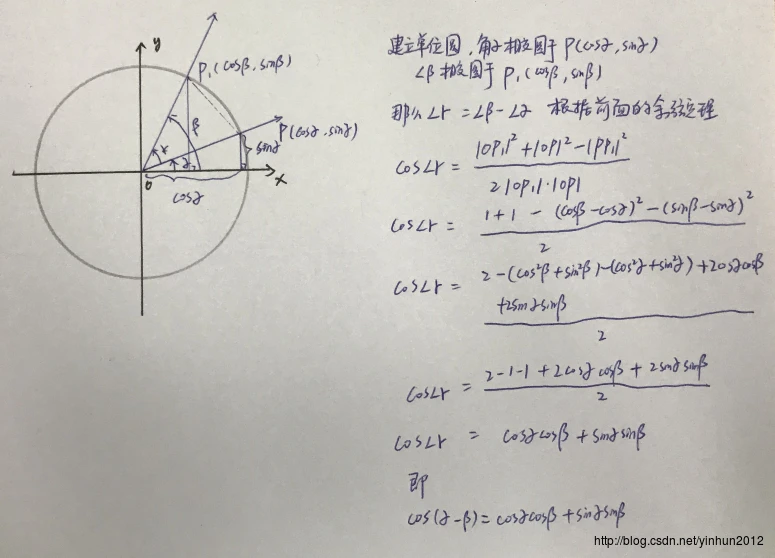
上面我们建立辅助用的单位圆,然后根据余弦定理推导了最简单的cos(α-β) = cosαcosβ+sinαsinβ,接下来继续推导,如下图:

这里我们用γ = -β去做替换,就能得到cos(α+γ) = cosαcosγ - sinαsinγ
既然cos推导完毕,接下来我们推到sin,前面我们推过:
sinα = -cos(90°+α)
cosα = sin(90°+α)
接下来我们继续用代换法,如下图:
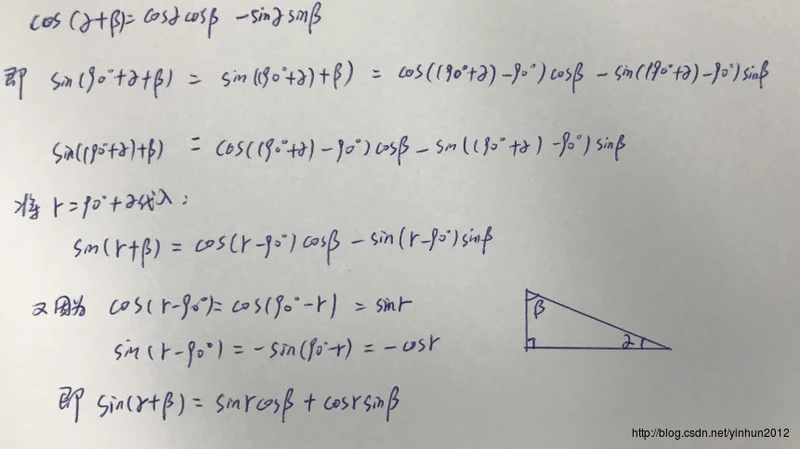
上面我们继续使用γ = 90°+α带入,然后利用直角三角形内角公式可以得出:
sin(α+β) = sinαcosβ + cosαsinβ
已经推导到这里了,那么最后的sin(α-β) = ?,这就简单了,只需要带入γ = -β就能得出:
sin(α-(-β)) = sinαcos(-(-β)) - cosαsin(-(-β))
因为γ = -β
所以
sin(α-γ) = sinαcos(-γ)-cosαsin(-γ)
sin(α-γ) = sinαcosγ + cosαsinγ
推导到这里
我们就知道sin75° = sin30°cos45° + cos30°sin45°
最后我们就用程序测试一下呗,如图:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class AngleMathFunc : MonoBehaviour
{
void Start()
{
int angle = 75;
//计算cos(α+γ) = cosαcosγ - sinαsinγ
float cosangle = Mathf.Cos(30) * Mathf.Cos(45) - Mathf.Sin(30) * Mathf.Sin(45);
float apicosangle = Mathf.Cos(angle);
#if UNITY_EDITOR
Debug.LogFormat("cosangle = {0} apicosangle = {1}", cosangle, apicosangle);
#endif
//计算sin(α+β) = sinαcosβ + cosαsinβ
float sinangle = Mathf.Sin(30) * Mathf.Cos(45) + Mathf.Cos(30) * Mathf.Sin(45);
float apisinangle = Mathf.Sin(angle);
#if UNITY_EDITOR
Debug.LogFormat("sinangle = {0} apisinangle = {1}", sinangle, apisinangle);
#endif
}
}
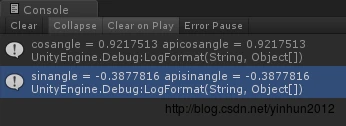
可以看出公式计算结果和函数api计算结果是一样的
