1 分圆多项式的理解
互素或互质(Coprime Integers): 若整数
a
a
a与整数
b
b
b的唯一公约数为
1
1
1,则称
a
a
a与
b
b
b互素或互质(coprime integers)。因此,任何能被
a
a
a整除的质数都不能被
b
b
b整除,反之亦然。也即两者的最大公约数(Greatest Common Divisor, GCD)为
1
1
1。
简单描述:分圆多项式可以简单理解为多项式
x
n
−
1
x^n - 1
xn−1分解后,所得的不可约多项式。
正式定义为:在数论中,对于任意正整数
n
n
n,
n
n
n次分圆多项式(nth cyclotomic polynomial)是一个具有整数系数的唯一不可约多项式
ϕ
n
(
x
)
\phi_n(x)
ϕn(x)(the unique irreducible polynomial with integer coefficients)。其中,对于任何
k
<
n
k < n
k<n,
ϕ
n
(
x
)
\phi_n(x)
ϕn(x)是
x
n
−
1
x^n-1
xn−1的一个因子,但不是
x
k
−
1
x^k-1
xk−1的一个因子。该分园多项式的根为n次原语单元根(nth primitive roots of unity)
e
2
i
π
k
n
e^{2i\pi \frac{k}{n}}
e2iπnk,其中,
k
k
k为不大于
n
n
n的正整数,且
k
k
k与
n
n
n为互质数。换句话说,
n
n
n次分圆多项式(nth cyclotomic polynomial)为:
ϕ n ( x ) = ∏ 1 ≤ k ≤ n g c d ( k , n ) = 1 ( x − e 2 i π k n ) \phi_n(x) = \displaystyle\prod_{1≤k≤n \atop gcd(k,n)=1}(x - e^{2i\pi \frac{k}{n}}) ϕn(x)=gcd(k,n)=11≤k≤n∏(x−e2iπnk)
2 举例说明计算方式
因计算过程中,常使用到 c o s / s i n cos/sin cos/sin的计算,结合下图可快速得出它们的结果。
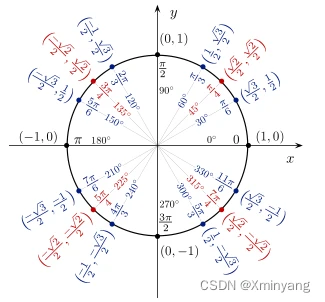
复数计算1:由于 e i θ = c o s ( θ ) + i ⋅ s i n ( θ ) e^{i\theta} = cos(\theta) + i \cdot sin(\theta) eiθ=cos(θ)+i⋅sin(θ),可得 e 2 i π k n = c o s ( 2 π k n ) + i ⋅ s i n ( 2 π k n ) e^{2i\pi \frac{k}{n}}=cos(2\pi \frac{k}{n}) + i \cdot sin(2\pi \frac{k}{n}) e2iπnk=cos(2πnk)+i⋅sin(2πnk)
复数计算2: i 2 = − 1 i^2=-1 i2=−1
2.1 演算 ϕ 1 ( x ) = x − 1 \phi_1(x) = x - 1 ϕ1(x)=x−1
- 仅存在一种情况:
n
=
1
,
k
=
1
n=1, k=1
n=1,k=1
因 c o s ( 2 π ) + i ⋅ s i n ( 2 π ) = 1 cos(2\pi) + i \cdot sin(2\pi) = 1 cos(2π)+i⋅sin(2π)=1,所以 ϕ 1 ( x ) = x − 1 \phi_1(x) = x - 1 ϕ1(x)=x−1
2.2 演算 ϕ 2 ( x ) = x + 1 \phi_2(x) = x + 1 ϕ2(x)=x+1
- 仅存在一种情况:
n
=
2
,
k
=
1
n=2, k=1
n=2,k=1
因 c o s ( π ) + i ⋅ s i n ( π ) = − 1 cos(\pi) + i \cdot sin(\pi) = -1 cos(π)+i⋅sin(π)=−1,所以 ϕ 2 ( x ) = x + 1 \phi_2(x) = x + 1 ϕ2(x)=x+1
2.3 演算 ϕ 3 ( x ) = x 2 + x + 1 \phi_3(x) = x^2 + x + 1 ϕ3(x)=x2+x+1
- 情况
1
1
1:
n
=
3
,
k
=
1
n=3, k=1
n=3,k=1
因 c o s ( 2 π 3 ) + i ⋅ s i n ( 2 π 3 ) = − 1 2 + 3 2 ⋅ i cos(\frac{2\pi}{3}) + i \cdot sin(\frac{2\pi}{3}) = -\frac{1}{2} + \frac{\sqrt{3}}{2} \cdot i cos(32π)+i⋅sin(32π)=−21+23⋅i - 情况
2
2
2:
n
=
3
,
k
=
2
n=3, k=2
n=3,k=2
因 c o s ( 4 π 3 ) + i ⋅ s i n ( 4 π 3 ) = − 1 2 − 3 2 ⋅ i cos(\frac{4\pi}{3}) + i \cdot sin(\frac{4\pi}{3}) = -\frac{1}{2} - \frac{\sqrt{3}}{2} \cdot i cos(34π)+i⋅sin(34π)=−21−23⋅i
所以 ϕ 3 ( x ) = ( x + 1 2 − 3 2 ⋅ i ) ⋅ ( x + 1 2 + 3 2 ⋅ i ) = ( x + 1 2 ) 2 − ( 3 2 ⋅ i ) 2 = x 2 + x + 1 4 − ( − 3 4 ) = x 2 + x + 1 \phi_3(x) = (x + \frac{1}{2} - \frac{\sqrt{3}}{2} \cdot i) \cdot (x + \frac{1}{2} + \frac{\sqrt{3}}{2} \cdot i) ={(x + \frac{1}{2})^2} -{(\frac{\sqrt{3}}{2} \cdot i)^2} =x^2 + x +\frac{1}{4} -{(-\frac{3}{4})}=x^2 + x + 1 ϕ3(x)=(x+21−23⋅i)⋅(x+21+23⋅i)=(x+21)2−(23⋅i)2=x2+x+41−(−43)=x2+x+1
2.4 演算 ϕ 4 ( x ) = x 2 + 1 \phi_4(x) = x^2 + 1 ϕ4(x)=x2+1
- 情况
1
1
1:
n
=
4
,
k
=
1
n=4, k=1
n=4,k=1
因 c o s ( π 2 ) + i ⋅ s i n ( π 2 ) = i cos(\frac{\pi}{2}) + i \cdot sin(\frac{\pi}{2}) = i cos(2π)+i⋅sin(2π)=i - 情况
2
2
2:
n
=
4
,
k
=
3
n=4, k=3
n=4,k=3
因 c o s ( 3 π 2 ) + i ⋅ s i n ( 3 π 2 ) = − i cos(\frac{3\pi}{2}) + i \cdot sin(\frac{3\pi}{2}) = -i cos(23π)+i⋅sin(23π)=−i
所以 ϕ 4 ( x ) = ( x − i ) ⋅ ( x + i ) = x 2 − ( − 1 ) = x 2 + 1 \phi_4(x) = (x - i) \cdot (x + i) =x^2 -{(-1)}=x^2 + 1 ϕ4(x)=(x−i)⋅(x+i)=x2−(−1)=x2+1
同理,可得 ϕ 5 ( x ) , ϕ 6 ( x ) . . . \phi_5(x),\phi_6(x)... ϕ5(x),ϕ6(x)...
综述,从 1 1 1到 30 30 30的分圆多项式为:

3 有趣的性质
3.1 同态加密常用的一个性质
- ϕ 2 h ( x ) = x 2 ( h − 1 ) + 1 \phi_{2^{h}}(x) = x^{{2}^{(h-1)}} + 1 ϕ2h(x)=x2(h−1)+1
因此,若 N = 2 k N= 2^k N=2k,则 2 N 2N 2N次分圆多项式为:
ϕ 2 N ( X ) = X N + 1 \phi_{2N}(X) = X^{N} + 1 ϕ2N(X)=XN+1
4 单位根
待完善
参考材料
- Wikipedia: Cyclotomic Polynomial
- Coprime integers - Wikipedia
- Prime number - Wikipedia
