目录
1定积分的概念
1.1定积分的定义
1.2定积分定理
2 定积分的性质
性质1 线性运算性
性质2 积分可加性
性质3
性质4 比较定理
性质5 估值定理
性质6 积分中值定理
1定积分的概念
1.1定积分的定义
设函数f(x)在[a,b]上有界，用分点a= x0< x1< x2<…<xn-1< xn=b 将区间[a, b]任意分成n个小区间:x0, x1, x1, x2, … [xn-1, xn],
第i的小区[xi-1, xi]的长度为∆xi=xi- xi-1 , 在其上任取一点ξi, 作乘积f(ξi) ∆xi (I = 1,2,…n), 并作和
,
如果不论对[a,b]怎样分法，也不论ξiϵ[xi-1, xi] 怎样取法， 极限
总存在且唯一，则称此极限为f(x) 在[a,b]上的定积分（简称积分），
，
其中∫ 称为积分号，f(x)称为被积函数，f(x)dx称为被积表达式，x称为积分变量，[a, b]为积分区间， a和b称为积分下限和积分上限，
称为积分和。
积分的定义包含了“分割，近似代替，求和，取极限”这样一个过程，其思想是化整体为对局部进行累积，在局部将变量近似为常量，再计算极限将近似转化为精确，其过程充分体现了整体与局部，变量和常量，近似与精确，量变与质变等矛盾对立统一的辩证法。
1.2定积分定理
定理1 设f(x)在[a, b]上连续，则f(x)在[a,b]上可积。
定理2 设f(x)在[a, b]上有界，且只有有限个间断点，则f(x)在[a,b]上可积。
- 当a=b时，
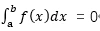
- 当a >b时，
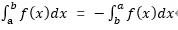
2 定积分的性质
性质1 线性运算性
设k1 k2为两个任意常数，则
性质2 积分可加性
不论a,b,c的相对位置如何，上述等式总成立。
性质3
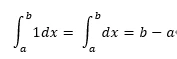
性质4 比较定理
若在[a,b]上，f(x) ≥ g(x), 则
若在[a,b]上，f(x) ≥0, 
性质5 估值定理
设M和m分别是函数f(x)在[a,b]上的最大值和最小值，则：
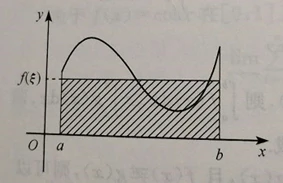
性质6 积分中值定理
若f(x)在[a,b]上连续，则在[a,b]上至少存在一点ξ， 使得 
.
积分中值定理的几何意义是：在[a,b]上至少存在一点ξ， 使得以区间[a,b]为底边，以f(x)为曲边的曲边梯形的面积等于同一底边而高为fξ的一个矩形的面积。如下图
