r语言常用数学函数有哪些

1.+ - * / ^

2.%/%，%%和%*%

3.ceiling,floor,round

4.signif,trunc,zapsamll

5.max,min,mean,pmax,pmin

6.range和sum

7.prod

8.cumsum,cumprod,cummax,cummin

9.sort

10. approx

11.approx fun

12.diff

13.sign

14.var和sd

15.median

16.IQR

17.ave

18.fivenum

19.mad

20.quantile

21.stem

22.描述性统计函数

23.频数统计函数：先分组，在计算频数

24.独立性检验

25.相关性分析

26.相关性检验函数

27.偏度和峰度

28.一维优化与求根

29.常用数学函数

30.高级数学函数

1.+ - * / ^

1.5 + 2.3 - 0.6 + 2.1*1.2 - 1.5/0.5 + 2^3

## [1] 10.72


#可以用圆括号改变优先级
1.5 + 2.3 - (0.6 + 2.1)*1.2 - 1.5/0.5 + 2^3


## [1] 5.56

2.%/%，%%和%*%

5 %/% 3
## [1] 1
5 %% 3
## [1] 2
5.1 %/% 2.5
## [1] 2
5.1 %% 2.5
## [1] 0.1

补充%*%
>m<-rbind(c(1,4),c(2,2))
> m
     [,1] [,2]
[1,]    1    4
[2,]    2    2
#计算向量(1,1)和m的矩阵积
> m%*%c(1,1)
     [,1]
[1,]    5
[2,]    4

3.ceiling,floor,round

#"ceiling"函数将输入的数字向上取整，返回大于或等于输入值的最小整数。

ceiling(3.14) # 输出 4
ceiling(-2.5) # 输出 -2

#"floor"函数将输入的数字向下取整，返回小于或等于输入值的最大整数。

floor(3.14) # 输出 3
floor(-2.5) # 输出 -3

#"round"函数将输入的数字四舍五入为最接近的整数。

round(3.14) # 输出 3
round(-2.5) # 输出 -2

#round第二个参数,指定要保留的位数
round(3.14159, 2)将返回保留两位小数的结果：3.14

4.signif,trunc,zapsamll

#signif函数用于保留指定有效数字位数
#它将输入的数字四舍五入到指定位数，并返回结果

signif(3.14159, 3) # 输出 3.14
signif(1234.5678, 2) # 输出 1200

#trunc函数截断（向零取整）输入的数字，即将小数部分去掉

trunc(3.14) # 输出 3
trunc(-2.5) # 输出 -2


#zapsmall函数用于移除非常接近零的小数误差
#它将输入的数字中非常小的值替换为零

zapsmall(1e-10) # 输出 0
zapsmall(0.000000001) # 输出 0

5.max,min,mean,pmax,pmin

#max函数用于计算一组数中的最大值
#它接受多个参数或一个向量作为输入，并返回其中的最大值。

max(2, 5, 1) # 输出 5
max(c(4, 6, 3)) # 输出 6

#min函数用于计算一组数中的最小值
#它接受多个参数或一个向量作为输入，并返回其中的最小值。

min(2, 5, 1) # 输出 1
min(c(4, 6, 3)) # 输出 3

# 计算向量的平均值
x <- c(1, 2, 3, 4, 5)
avg <- mean(x)

print(avg)
#输出 [1] 3

#pmax函数用于逐个比较两个或多个向量中的相应元素
#并返回对应位置上的最大值向量

pmax(c(1, 3, 5), c(2, 4, 6)) # 输出 2 4 6
pmax(c(1, 3, 5), c(2, 4, 6), c(0, 8, 7)) # 输出 2 8 7

#pmin函数用于逐个比较两个或多个向量中的相应元素
#并返回对应位置上的最小值向量

pmin(c(1, 3, 5), c(2, 4, 6)) # 输出 1 3 5
pmin(c(1, 3, 5), c(2, 4, 6), c(0, 8, 7)) # 输出 0 3 5

6.range和sum

#返回一个包含最小值和最大值的长度为2的向量

range(c(2, 5, 1)) # 输出 1 5
range(1:10) # 输出 1 10

#sum函数用于计算给定向量或数值序列的总和
#它接受一个向量作为输入，并返回所有元素的累加和

sum(c(2, 5, 1)) # 输出 8
sum(1:10) # 输出 55

7.prod

#prod是用于计算一组数的乘积的函数

prod(c(2, 3, 4)) # 输出 24，即 2 * 3 * 4

#如果向量中存在0，则结果将始终为0

prod(c(2, 0, 4)) # 输出 0，因为存在0

#同样，如果向量中有任何非数值（例如字符或缺失值）
则结果将为NA（不可用）

prod(c(2, "a", 4)) # 输出 NA，因为存在非数值元素

8.cumsum,cumprod,cummax,cummin

#cumsum函数用于计算给定向量或数值序列中元素的累积和

cumsum(c(2, 3, 4)) 
# 输出 2 5 9，即 2, 2+3, 2+3+4

#cumprod函数用于计算给定向量或数值序列中元素的累积乘积

cumprod(c(2, 3, 4)) 
# 输出 2 6 24，即 2, 2*3, 2*3*4

#cummax函数用于计算给定向量或数值序列中元素的累积最大值

cummax(c(2, 3, 4, 1, 5)) 
# 输出 2 3 4 4 5，即 2, max(2,3), max(2,3,4), max(2,3,4,1), max(2,3,4,5)

#cummin函数用于计算给定向量或数值序列中元素的累积最小值

cummin(c(2, 3, 4, 1, 5)) 
# 输出 2 2 2 1 1，即 2, min(2,3), min(2,3,4), min(2,3,4,1),min(2,3,4,1,5)

9.sort

(1)对向量排序

sort(c(3, 1, 4, 2)) # 输出 1 2 3 4

(2) 降序排序

sort(c(3, 1, 4, 2), decreasing = TRUE) # 输出 4 3 2 1

(3) 对数据框按照某列进行排序

df <- data.frame(x = c(3, 1, 4, 2), y = c("A", "B", "C", "D"))
sorted_df$x # 获取排序后的 x 列
sorted_df$y # 获取排序后的 y 列
sorted_df[1, ] # 获取排序后的第一行数据

(4) 降序排序

sorted_df <- df[order(df$x, decreasing = TRUE), ] # 按 x 列降序排序

10. approx

#approx函数用于执行线性插值或平滑插值
approx(x, y = NULL, xout, method = "linear", rule = 2, f = 0, ties = mean)

常用参数

x：输入变量的向量。
y：输出变量的向量。当进行插值时，需要提供此参数。
xout：用于进行估计或插值的输出变量的取值点。这是一个可选的参数。
method：指定插值方法，默认为"linear"（线性插值）。还可以选择"constant"（常数插值）或"spline"（样条插值）等。
rule：在估计或插值点不在输入变量范围内时的处理规则。它控制如何对缺失值或超出范围的值进行处理。默认为2，表示生成具有最小相对误差的结果。
f：自定义函数，用于在估计或插值点上执行特定的计算。
ties：用于处理在估计或插值点存在多个匹配的情况下如何处理。
"ordered"：根据输入变量 x 的顺序，按照与估计或插值点最接近的方式处理匹配值。默认情况下，ties参数设置为"mean"。
"mean"：将匹配值的平均值作为结果。如果有多个匹配值，将它们的平均值用于计算结果。
"min"：选择匹配值中的最小值作为结果。
"max"：选择匹配值中的最大值作为结果。

# 创建输入数据
x <- c(1, 2, 4, 5)  # 输入变量 x
y <- c(3, 6, 2, 8)  # 输出变量 y

# 进行线性插值
interp <- approx(x, y, xout = seq(min(x), max(x), by = 0.1))

# 输出结果
print(interp)

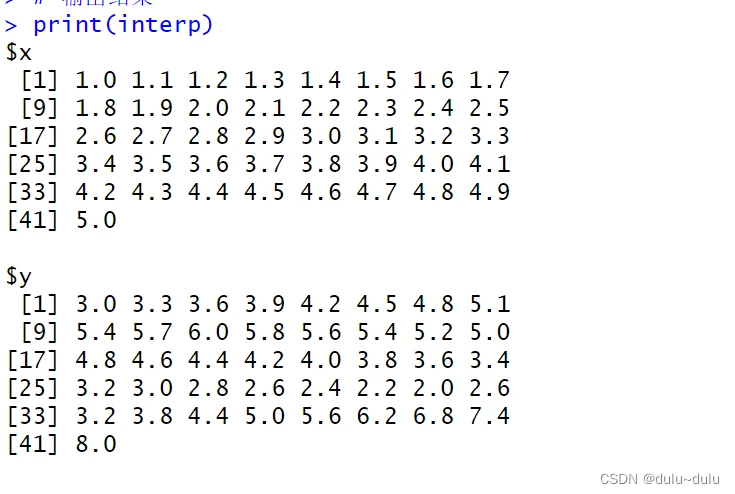
11.approx fun

# 自定义函数
my_fun <- function(x, y) {
  return(x^2 + y)
}

# 创建输入数据
x <- c(1, 2, 4, 5)
y <- c(3, 6, 2, 8)

# 使用自定义函数进行插值
interp <- approx(x, y, xout = seq(min(x), max(x), by = 0.1), f = my_fun)

# 输出结果
print(interp)

12.diff

#diff函数用于计算向量或时间序列的差分
#对于长度为 n 的向量，diff函数将返回一个长度为 n-1 的向量
#其中第 i 个元素是原始向量中第 (i+1) 个元素减去第 i 个元素的结果。
vec <- c(2, 6, 5, 8, 3)

diff_vec <- diff(vec)

print(diff_vec)

#输出 [1]  4 -1  3 -5

13.sign

sign函数用于返回给定数值的符号

如果输入值大于0，则返回1。
如果输入值等于0，则返回0。
如果输入值小于0，则返回-1。

num <-  -5

sign_num <- sign(num)

print(sign_num)

#输出 [1] -1
#因为-5是一个负数

14.var和sd

# 计算向量的方差和标准差
x <- c(1, 2, 3, 4, 5)

variance <- var(x)
standard_deviation <- sd(x)

print(variance)
print(standard_deviation)

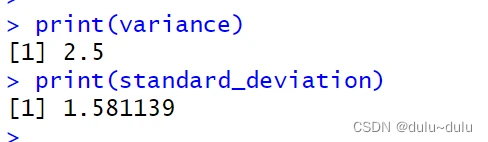
15.median

# 计算向量的中位数
x <- c(1, 2, 3, 4, 5)

median_value <- median(x)

print(median_value)

#输出 [1] 3

16.IQR

# 计算向量的四分位距
x <- c(1, 2, 3, 4, 5)

iqr_value <- IQR(x)

print(iqr_value)

#输出 [1] 2

17.ave

用于根据某个变量对向量或数据框进行分组，并对每个组应用函数

# 创建一个数据框
df <- data.frame(
  name = c("Alice", "Bob", "Alice", "Charlie", "Charlie", "Bob"),
  score = c(85, 90, 92, 78, 80, 88)
)

# 对数据框中的 score 列按 name 分组，计算每个组的平均值
average_scores <- ave(df$score, df$name, FUN = mean)

print(average_scores)

18.fivenum

# 计算向量的五数概括统计量
#包括最小值、下四分位数、中位数、上四分位数和最大值
x <- c(1, 2, 3, 4, 5)

fivenum_values <- fivenum(x)

print(fivenum_values)

19.mad

# 计算向量的绝对中位差
x <- c(1, 2, 3, 4, 5)

mad_value <- mad(x)

print(mad_value)

20.quantile

# 计算向量的分位数
x <- c(1, 2, 3, 4, 5)

# 计算四分位数
quartiles <- quantile(x, probs = c(0.25, 0.5, 0.75))

print(quartiles)

21.stem

# 创建茎叶图
x <- c(12, 23, 34, 45, 56, 67, 78, 89, 90)

stem(x)

22.描述性统计函数

（1）summary

> myvars<-mtcars[c("mpg","hp","wt","am")]
> summary(myvars)
      mpg              hp              wt              am        
 Min.   :10.40   Min.   : 52.0   Min.   :1.513   Min.   :0.0000  
 1st Qu.:15.43   1st Qu.: 96.5   1st Qu.:2.581   1st Qu.:0.0000  
 Median :19.20   Median :123.0   Median :3.325   Median :0.0000  
 Mean   :20.09   Mean   :146.7   Mean   :3.217   Mean   :0.4062  
 3rd Qu.:22.80   3rd Qu.:180.0   3rd Qu.:3.610   3rd Qu.:1.0000  
 Max.   :33.90   Max.   :335.0   Max.   :5.424   Max.   :1.0000  
> fivenum(myvars$hp)
[1]  52  96 123 180 335

补充：skim

#能够返回更加详细的信息，信息量过多不好复制，可以自己尝试一下

library(skimr)

skim(d)

（2）decribe

describe有两种类型：

#第一种类型
> library(Hmisc)
> describe(myvars)
myvars 

 4  Variables      32  Observations
----------------------------------------------------------------------------
mpg 
       n  missing distinct     Info     Mean      Gmd      .05      .10 
      32        0       25    0.999    20.09    6.796    12.00    14.34 
     .25      .50      .75      .90      .95 
   15.43    19.20    22.80    30.09    31.30 

lowest : 10.4 13.3 14.3 14.7 15  , highest: 26   27.3 30.4 32.4 33.9
----------------------------------------------------------------------------
hp 
       n  missing distinct     Info     Mean      Gmd      .05      .10 
      32        0       22    0.997    146.7    77.04    63.65    66.00 
     .25      .50      .75      .90      .95 
   96.50   123.00   180.00   243.50   253.55 

52 (1, 0.031), 60.49 (1, 0.031), 63.32 (3, 0.094), 88.79 (1, 0.031), 91.62
(1, 0.031), 94.45 (2, 0.062), 102.94 (1, 0.031), 108.6 (4, 0.125), 111.43
(1, 0.031), 122.75 (2, 0.062), 148.22 (2, 0.062), 173.69 (3, 0.094), 179.35
(3, 0.094), 204.82 (1, 0.031), 213.31 (1, 0.031), 227.46 (1, 0.031), 244.44
(2, 0.062), 261.42 (1, 0.031), 335 (1, 0.031)

For the frequency table, variable is rounded to the nearest 2.83
----------------------------------------------------------------------------
wt 
       n  missing distinct     Info     Mean      Gmd      .05      .10 
      32        0       29    0.999    3.217    1.089    1.736    1.956 
     .25      .50      .75      .90      .95 
   2.581    3.325    3.610    4.048    5.293 

lowest : 1.513 1.615 1.835 1.935 2.14 , highest: 3.845 4.07  5.25  5.345 5.424
----------------------------------------------------------------------------
am 
       n  missing distinct     Info      Sum     Mean      Gmd 
      32        0        2    0.724       13   0.4062    0.498 

----------------------------------------------------------------------------
#第二种类型
> psych::describe(myvars)
    vars  n   mean    sd median trimmed   mad   min    max  range skew kurtosis    se
mpg    1 32  20.09  6.03  19.20   19.70  5.41 10.40  33.90  23.50 0.61    -0.37  1.07
hp     2 32 146.69 68.56 123.00  141.19 77.10 52.00 335.00 283.00 0.73    -0.14 12.12
wt     3 32   3.22  0.98   3.33    3.15  0.77  1.51   5.42   3.91 0.42    -0.02  0.17
am     4 32   0.41  0.50   0.00    0.38  0.00  0.00   1.00   1.00 0.36    -1.92  0.09

注：后面使用的包中的函数会覆盖之前不同包中同样的函数

（3）stat.desc

> library(pastecs)

> stat.desc(myvars)
                     mpg           hp          wt          am
nbr.val       32.0000000   32.0000000  32.0000000 32.00000000
nbr.null       0.0000000    0.0000000   0.0000000 19.00000000
nbr.na         0.0000000    0.0000000   0.0000000  0.00000000
min           10.4000000   52.0000000   1.5130000  0.00000000
max           33.9000000  335.0000000   5.4240000  1.00000000
range         23.5000000  283.0000000   3.9110000  1.00000000
sum          642.9000000 4694.0000000 102.9520000 13.00000000
median        19.2000000  123.0000000   3.3250000  0.00000000
mean          20.0906250  146.6875000   3.2172500  0.40625000
SE.mean        1.0654240   12.1203173   0.1729685  0.08820997
CI.mean.0.95   2.1729465   24.7195501   0.3527715  0.17990541
var           36.3241028 4700.8669355   0.9573790  0.24899194
std.dev        6.0269481   68.5628685   0.9784574  0.49899092
coef.var       0.2999881    0.4674077   0.3041285  1.22828533
> stat.desc(myvars,basic = T)
                     mpg           hp          wt          am
nbr.val       32.0000000   32.0000000  32.0000000 32.00000000
nbr.null       0.0000000    0.0000000   0.0000000 19.00000000
nbr.na         0.0000000    0.0000000   0.0000000  0.00000000
min           10.4000000   52.0000000   1.5130000  0.00000000
max           33.9000000  335.0000000   5.4240000  1.00000000
range         23.5000000  283.0000000   3.9110000  1.00000000
sum          642.9000000 4694.0000000 102.9520000 13.00000000
median        19.2000000  123.0000000   3.3250000  0.00000000
mean          20.0906250  146.6875000   3.2172500  0.40625000
SE.mean        1.0654240   12.1203173   0.1729685  0.08820997
CI.mean.0.95   2.1729465   24.7195501   0.3527715  0.17990541
var           36.3241028 4700.8669355   0.9573790  0.24899194
std.dev        6.0269481   68.5628685   0.9784574  0.49899092
coef.var       0.2999881    0.4674077   0.3041285  1.22828533

> stat.desc(myvars,norm = T)
                     mpg            hp           wt            am
nbr.val       32.0000000   32.00000000  32.00000000  3.200000e+01
nbr.null       0.0000000    0.00000000   0.00000000  1.900000e+01
nbr.na         0.0000000    0.00000000   0.00000000  0.000000e+00
min           10.4000000   52.00000000   1.51300000  0.000000e+00
max           33.9000000  335.00000000   5.42400000  1.000000e+00
range         23.5000000  283.00000000   3.91100000  1.000000e+00
sum          642.9000000 4694.00000000 102.95200000  1.300000e+01
median        19.2000000  123.00000000   3.32500000  0.000000e+00
mean          20.0906250  146.68750000   3.21725000  4.062500e-01
SE.mean        1.0654240   12.12031731   0.17296847  8.820997e-02
CI.mean.0.95   2.1729465   24.71955013   0.35277153  1.799054e-01
var           36.3241028 4700.86693548   0.95737897  2.489919e-01
std.dev        6.0269481   68.56286849   0.97845744  4.989909e-01
coef.var       0.2999881    0.46740771   0.30412851  1.228285e+00
skewness       0.6106550    0.72602366   0.42314646  3.640159e-01
skew.2SE       0.7366922    0.87587259   0.51048252  4.391476e-01
kurtosis      -0.3727660   -0.13555112  -0.02271075 -1.924741e+00
kurt.2SE      -0.2302812   -0.08373853  -0.01402987 -1.189035e+00
normtest.W     0.9475647    0.93341934   0.94325772  6.250744e-01
normtest.p     0.1228814    0.04880824   0.09265499  7.836354e-08

(4)aggregate

> library(doBy)
> summaryBy(mpg+hp+wt ~ am,data=myvars,FUN = mean)
  am mpg.mean  hp.mean  wt.mean
1  0 17.14737 160.2632 3.768895
2  1 24.39231 126.8462 2.411000


> library(psych)
#describe的缺点就是每个统计值都是固定的,没办法自定义函数
> describe.by(myvars,list(am=mtcars$am))

 Descriptive statistics by group 
am: 0
    vars  n   mean    sd median trimmed   mad   min    max  range  skew kurtosis    se
mpg    1 19  17.15  3.83  17.30   17.12  3.11 10.40  24.40  14.00  0.01    -0.80  0.88
hp     2 19 160.26 53.91 175.00  161.06 77.10 62.00 245.00 183.00 -0.01    -1.21 12.37
wt     3 19   3.77  0.78   3.52    3.75  0.45  2.46   5.42   2.96  0.98     0.14  0.18
am     4 19   0.00  0.00   0.00    0.00  0.00  0.00   0.00   0.00   NaN      NaN  0.00
--------------------------------------------------------------------- 
am: 1
    vars  n   mean    sd median trimmed   mad   min    max  range skew kurtosis    se
mpg    1 13  24.39  6.17  22.80   24.38  6.67 15.00  33.90  18.90 0.05    -1.46  1.71
hp     2 13 126.85 84.06 109.00  114.73 63.75 52.00 335.00 283.00 1.36     0.56 23.31
wt     3 13   2.41  0.62   2.32    2.39  0.68  1.51   3.57   2.06 0.21    -1.17  0.17
am     4 13   1.00  0.00   1.00    1.00  0.00  1.00   1.00   0.00  NaN      NaN  0.00

> library(MASS)
#根据Manufacturer进行分组，并且计算每个Price的均值
>aggregate(Cars93[c("Min.Price","Price","Max.Price","MPG.city")],by=list(Manufacture=Cars93$Manufacturer),mean)

aggregate一次只能计算一个统计函数，例如上面的示例，只能使用mean

可以使用如下函数：

23.频数统计函数：先分组，在计算频数

（1）分组

split

mtcars$cyl<-as.factor(mtcars$cyl)
> split(mtcars,mtcars$cyl)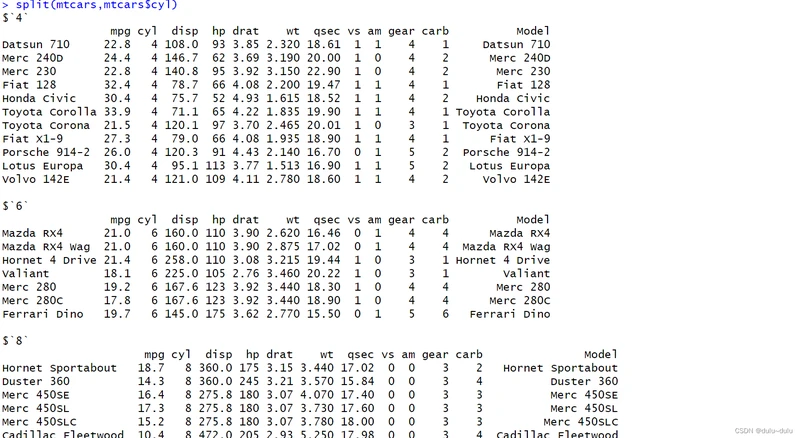

cut

> cut(mtcars$mpg,c(seq(10,50,10)))
 [1] (20,30] (20,30] (20,30] (20,30] (10,20] (10,20] (10,20] (20,30] (20,30] (10,20] (10,20]
[12] (10,20] (10,20] (10,20] (10,20] (10,20] (10,20] (30,40] (30,40] (30,40] (20,30] (10,20]
[23] (10,20] (10,20] (10,20] (20,30] (20,30] (30,40] (10,20] (10,20] (10,20] (20,30]
Levels: (10,20] (20,30] (30,40] (40,50]

(2) 频数统计

#一维
> table(cut(mtcars$mpg,c(seq(10,50,10))))

(10,20] (20,30] (30,40] (40,50] 
     18      10       4       0 

> prop.table(table(mtcars$cyl))

      4       6       8 
0.34375 0.21875 0.43750 

#二维
> table(Arthritis$Treatment,Arthritis$Improved)
         
          None Some Marked
  Placebo   29    7      7
  Treated   13    7     21

> with(data=Arthritis,(table(Treatment,Improved)))
         Improved
Treatment None Some Marked
  Placebo   29    7      7
  Treated   13    7     21
#~表示公式省略
> xtabs(~Treatment+Improved,data=Arthritis)
         Improved
Treatment None Some Marked
  Placebo   29    7      7
  Treated   13    7     21

> x<-xtabs(~Treatment+Improved,data=Arthritis)
> margin.table(x)
[1] 84
#1表示计算的边际是针对行进行的，2表示计算的边际是针对列进行的
 margin.table(x,1)
Treatment
Placebo Treated 
     43      41 
> prop.table(x,2)
         Improved
Treatment      None      Some    Marked
  Placebo 0.6904762 0.5000000 0.2500000
  Treated 0.3095238 0.5000000 0.7500000
> prop.table(x,1)
         Improved
Treatment      None      Some    Marked
  Placebo 0.6744186 0.1627907 0.1627907
  Treated 0.3170732 0.1707317 0.5121951
> margin.table(x,2)
Improved
  None   Some Marked 
    42     14     28

24.独立性检验

步骤一：假设检验

原假设--没有发生
备择假设--发生了
具体作法:根据问题的需要对所研究的总体作某种假设，记作H0;选取合适的统计量，这个统计量的选取要使得在假设HO成立时，其分布为已知;由实测的样本，计算出统计量的值，并根据预先给定的显著性水平进行检验，作出拒绝或接受假设HO的判断。

步骤二：p-value检测是否接受或拒绝原假设

p-value
p-value就是Probability的值，它是一个通过计算得到的概率值，也就是在原假设为真时，得到最大的或者超出所得到的检验统计量值的概率
般将p值定位到0.05，当p<0.05拒绝原假设，p>0.05，不拒绝原假设

（1）卡方检验

> library(vcd)
> mytable<-table(Arthritis$Treatment,Arthritis$Improved)
> chisq.test(mytable)

	Pearson's Chi-squared test

data:  mytable
X-squared = 13.055, df = 2, p-value = 0.001463
#p-value--->0.001463:小于0.05,说明变量不独立

（2）Fisher检验

> mytable<-xtabs(~Treatment+Improved,data=Arthritis)
> fisher.test(mytable)

	Fisher's Exact Test for Count Data

data:  mytable
p-value = 0.001393
alternative hypothesis: two.sided

p-value=0.001393：说明变量不独立

（2）Cochran-Mantel-Haenszel检验

> mytable<-xtabs(~Treatment+Improved+Sex,data=Arthritis)
> mantelhaen.test(mytable)

	Cochran-Mantel-Haenszel test

data:  mytable
Cochran-Mantel-Haenszel M^2 = 14.632, df = 2, p-value = 0.0006647

#变量的顺序很重要,顺序变化,p-value也会变化
 mytable<-xtabs(~Treatment+Sex+Improved,data=Arthritis)
> mantelhaen.test(mytable)

	Mantel-Haenszel chi-squared test with continuity correction

data:  mytable
Mantel-Haenszel X-squared = 2.0863, df = 1, p-value = 0.1486
alternative hypothesis: true common odds ratio is not equal to 1
95 percent confidence interval:
 0.8566711 8.0070521
sample estimates:
common odds ratio 
         2.619048

25.相关性分析

（1）Person系数

#有很多相关系数的检验方法,默认为person相关系数
#正相关为+,负相关为-
> cor(state.x77)
            Population     Income  Illiteracy    Life Exp     Murder     HS Grad      Frost        Area
Population  1.00000000  0.2082276  0.10762237 -0.06805195  0.3436428 -0.09848975 -0.3321525  0.02254384
Income      0.20822756  1.0000000 -0.43707519  0.34025534 -0.2300776  0.61993232  0.2262822  0.36331544
Illiteracy  0.10762237 -0.4370752  1.00000000 -0.58847793  0.7029752 -0.65718861 -0.6719470  0.07726113
Life Exp   -0.06805195  0.3402553 -0.58847793  1.00000000 -0.7808458  0.58221620  0.2620680 -0.10733194
Murder      0.34364275 -0.2300776  0.70297520 -0.78084575  1.0000000 -0.48797102 -0.5388834  0.22839021
HS Grad    -0.09848975  0.6199323 -0.65718861  0.58221620 -0.4879710  1.00000000  0.3667797  0.33354187
Frost      -0.33215245  0.2262822 -0.67194697  0.26206801 -0.5388834  0.36677970  1.0000000  0.05922910
Area        0.02254384  0.3633154  0.07726113 -0.10733194  0.2283902  0.33354187  0.0592291  1.00000000

> x<-state.x77[,c(1,2,3,6)]
> y<-state.x77[,c(4,5)]
> cor(x,y)
              Life Exp     Murder
Population -0.06805195  0.3436428
Income      0.34025534 -0.2300776
Illiteracy -0.58847793  0.7029752
HS Grad     0.58221620 -0.4879710
>

（2）协方差

> cov(state.x77)
              Population        Income   Illiteracy      Life Exp       Murder       HS Grad        Frost          Area
Population 19931683.7588   571229.7796  292.8679592 -4.078425e+02  5663.523714  -3551.509551 -77081.97265  8.587917e+06
Income       571229.7796   377573.3061 -163.7020408  2.806632e+02  -521.894286   3076.768980   7227.60408  1.904901e+07
Illiteracy      292.8680     -163.7020    0.3715306 -4.815122e-01     1.581776     -3.235469    -21.29000  4.018337e+03
Life Exp       -407.8425      280.6632   -0.4815122  1.802020e+00    -3.869480      6.312685     18.28678 -1.229410e+04
Murder         5663.5237     -521.8943    1.5817755 -3.869480e+00    13.627465    -14.549616   -103.40600  7.194043e+04
HS Grad       -3551.5096     3076.7690   -3.2354694  6.312685e+00   -14.549616     65.237894    153.99216  2.298732e+05
Frost        -77081.9727     7227.6041  -21.2900000  1.828678e+01  -103.406000    153.992163   2702.00857  2.627039e+05
Area        8587916.9494 19049013.7510 4018.3371429 -1.229410e+04 71940.429959 229873.192816 262703.89306  7.280748e+09

（3）偏相关系数

> colnames(state.x77)
[1] "Population" "Income"     "Illiteracy" "Life Exp"   "Murder"     "HS Grad"   
[7] "Frost"      "Area"
#      
> pcor(c(1,5,2,3,6),cov(state.x77))
[1] 0.3462724

26.相关性检验函数

> colnames(state.x77)
[1] "Population" "Income"     "Illiteracy" "Life Exp"   "Murder"     "HS Grad"   
[7] "Frost"      "Area"      
> cor.test(state.x77[,3],state.x77[,5])

	Pearson's product-moment correlation

data:  state.x77[, 3] and state.x77[, 5]
t = 6.8479, df = 48, p-value = 1.258e-08
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.5279280 0.8207295
sample estimates:
      cor 
0.7029752 


#p-value为1.258e-8,拒绝原假设,相关系数不为零
#confidence interval(置信区间)
置信水平为95%的置信区间意味着我们有95%的置信度认为总体参数落在该区间内

#变量之间的相关关系
> library(psych)
> corr.test(state.x77)
Call:corr.test(x = state.x77)
Correlation matrix 
           Population Income Illiteracy Life Exp Murder HS Grad Frost  Area
Population       1.00   0.21       0.11    -0.07   0.34   -0.10 -0.33  0.02
Income           0.21   1.00      -0.44     0.34  -0.23    0.62  0.23  0.36
Illiteracy       0.11  -0.44       1.00    -0.59   0.70   -0.66 -0.67  0.08
Life Exp        -0.07   0.34      -0.59     1.00  -0.78    0.58  0.26 -0.11
Murder           0.34  -0.23       0.70    -0.78   1.00   -0.49 -0.54  0.23
HS Grad         -0.10   0.62      -0.66     0.58  -0.49    1.00  0.37  0.33
Frost           -0.33   0.23      -0.67     0.26  -0.54    0.37  1.00  0.06
Area             0.02   0.36       0.08    -0.11   0.23    0.33  0.06  1.00
Sample Size 
[1] 50
Probability values (Entries above the diagonal are adjusted for multiple tests.) 
           Population Income Illiteracy Life Exp Murder HS Grad Frost Area
Population       0.00   1.00       1.00     1.00   0.23    1.00  0.25 1.00
Income           0.15   0.00       0.03     0.23   1.00    0.00  1.00 0.16
Illiteracy       0.46   0.00       0.00     0.00   0.00    0.00  0.00 1.00
Life Exp         0.64   0.02       0.00     0.00   0.00    0.00  0.79 1.00
Murder           0.01   0.11       0.00     0.00   0.00    0.01  0.00 1.00
HS Grad          0.50   0.00       0.00     0.00   0.00    0.00  0.16 0.25
Frost            0.02   0.11       0.00     0.07   0.00    0.01  0.00 1.00
Area             0.88   0.01       0.59     0.46   0.11    0.02  0.68 0.00

 To see confidence intervals of the correlations, print with the short=FALSE option


> x<-pcor(c(1,5,2,3,6),cov(state.x77))
> x
[1] 0.3462724
#3个变量，50个样本数
> pcor.test(x,3,50)
$tval
[1] 2.476049

$df
[1] 45

$pvalue
[1] 0.01711252

检验方法

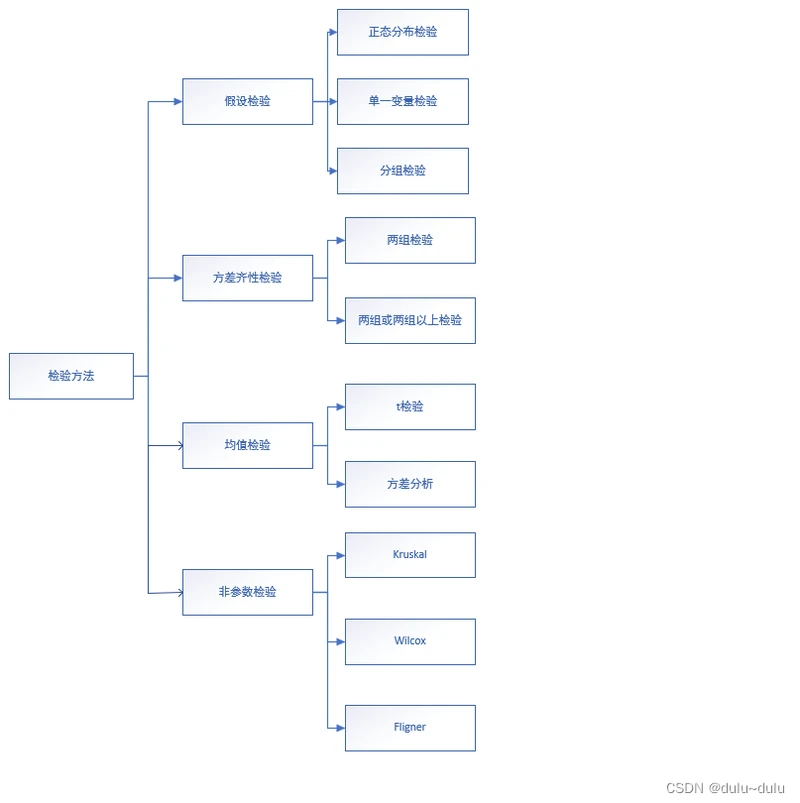
#假设检验

##正态分布检验
> head(ToothGrowth)
   len supp dose
1  4.2   VC  0.5
2 11.5   VC  0.5
3  7.3   VC  0.5
4  5.8   VC  0.5
5  6.4   VC  0.5
6 10.0   VC  0.5
##单一变量检验
> ToothGrowth%>%
+ shapiro_test(len)
# A tibble: 1 × 3
  variable statistic     p
  <chr>        <dbl> <dbl>
1 len          0.967 0.109
##分组检验
> ToothGrowth%>%
+ group_by(dose)%>%
+ shapiro_test(len)
# A tibble: 3 × 4
   dose variable statistic     p
  <dbl> <chr>        <dbl> <dbl>
1   0.5 len          0.941 0.247
2   1   len          0.931 0.164
3   2   len      

#方差齐性检验

##两组检验
> var.test(len~supp,data=ToothGrowth)

	F test to compare two variances

data:  len by supp
F = 0.6386, num df = 29, denom df = 29, p-value = 0.2331
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.3039488 1.3416857
sample estimates:
ratio of variances 
         0.6385951 
##两组及以上检验
> bartlett.test(len~dose,data=ToothGrowth)

	Bartlett test of homogeneity of variances

data:  len by dose
Bartlett's K-squared = 0.66547, df = 2, p-value = 0.717

#均值检验
##t检验：用于比较两个样本均值是否显著不同
> colnames(UScrime)
 [1] "M"    "So"   "Ed"   "Po1"  "Po2"  "LF"   "M.F"  "Pop"  "NW"   "U1"   "U2"  
[12] "GDP"  "Ineq" "Prob" "Time" "y"   
> t.test(Prob ~ So,data=UScrime)

	Welch Two Sample t-test

data:  Prob by So
t = -3.8954, df = 24.925, p-value = 0.0006506
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
 -0.03852569 -0.01187439
sample estimates:
mean in group 0 mean in group 1 
     0.03851265      0.06371269 

##方差分析
> ToothGrowth$dose<-as.factor(ToothGrowth$dose)
> aovfit<-aov(len~dose,data=ToothGrowth)
> aovfit
Call:
   aov(formula = len ~ dose, data = ToothGrowth)

Terms:
                    dose Residuals
Sum of Squares  2426.434  1025.775
Deg. of Freedom        2        57

Residual standard error: 4.242175
Estimated effects may be unbalanced
> summary(aovfit)
            Df Sum Sq Mean Sq F value   Pr(>F)    
dose         2   2426    1213   67.42 9.53e-16 ***
Residuals   57   1026      18                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> 

##非参数检验
#差异检验：wilcox秩和检验（Mann-whitney U检验）,适用于两组数据
> wilcox.test(len~supp,data=ToothGrowth)

	Wilcoxon rank sum test with continuity correction

data:  len by supp
W = 575.5, p-value = 0.06449
alternative hypothesis: true location shift is not equal to 0

#差异检验：Kruskal-wallis检验，适用于两组及以上检验
> kruskal.test(len~dose,data=ToothGrowth)

	Kruskal-Wallis rank sum test

data:  len by dose
Kruskal-Wallis chi-squared = 40.669, df = 2, p-value = 1.475e-09

#方差齐性非参数检验
> fligner.test(len~dose,data=ToothGrowth)

	Fligner-Killeen test of homogeneity of variances

data:  len by dose
Fligner-Killeen:med chi-squared = 1.3879, df = 2, p-value = 0.4996

27.偏度和峰度

 d3<-data.frame(
+     ind=1:1000,
+     rn=rnorm(1000),
+     rn2=rnorm(1000,mean = 2,sd=3),
+     rt=rt(1000,df=5),
+     rs1=as.factor(sample(letters[1:3],1000,replace=T)),                               
          rs2=as.factor(sample(letters[21:22],1000,replace=T))
)

#偏度
e1071::skewness(d3$rn)

#峰度
e1071::kurtosis(d3$rn2)

28.一维优化与求根

（1）optimize

optimize() 函数用于在给定区间内寻找一个函数的最小值或最大值。

#optimize(f, interval, maximum = FALSE, tol = .Machine$double.eps^0.25)

#f 是要最小化或最大化的函数；
#interval 是定义函数的有效区间。
#maximum：一个逻辑值，用于指定是寻找最小值还是最大值。默认为 FALSE，表示寻找最小值。
#tol：一个数值，表示收敛容差（convergence tolerance）。默认值为 .Machine$double.eps^0.25，使用机器精度的推荐容差。

f <- function(x) x^2 - 4 * x + 3

result <- optimize(f, c(0, 5))
print(result$minimum)  # 输出函数的最小值
#输出 [1] 2

（2）uniroot

uniroot() 函数用于在给定区间内寻找一个函数的根

#uniroot(f, interval)
#f 是要寻找根的函数；interval 是定义函数的有效区间
f <- function(x) x^3 - 2 * x - 5

result <- uniroot(f, c(1, 3))
print(result$root)  # 输出函数的根

#输出 [1] 2.094526

（3）polyroot

polyroot() 函数用于找到多项式函数的所有根

# polyroot(coeffs)
#coeffs 是一个包含多项式系数的向量

coeffs <- c(1, -5, 4)

roots <- polyroot(coeffs)
print(roots)  # 输出多项式函数的所有根

#输出 [1] 4+0i 1+0i

29.常用数学函数

#abs：获取数值的绝对值
abs(-5) # 输出 5
abs(3.14) # 输出 3.14

#sqrt：计算数值的平方根
sqrt(9) # 输出 3
sqrt(2) # 输出 1.414213 


#sin:正弦
sin(x)

#cos：余弦
cos(x)

#tan:正切
tan(x)

#asin:反正弦
asin(x)

#acos：反余弦
acos(x)

#atan:反正切
atan(x)

#atan2:给定y和x坐标的反正切
atan2(y,x)

#sinh:双曲正弦值
sinh(x)

#cosh：双曲余弦值
cosh(x)

#tanh:双曲正弦值
tanh(x)

#ashih:反双曲正弦值
ashih(x)

#acosh:反双曲余弦值
acosh(x)

#atanh:反双曲正切值
atanh(x)

30.高级数学函数

#beta函数：计算两个参数的Beta函数值

beta(x,y)

#lbeta函数：计算两个参数的Beta函数的自然对数

lbeta(x,y)

#gamma函数：计算给定参数的伽玛函数值

gamma(x)

#lgamma函数：计算给定参数的伽玛函数的自然对数

lgamma(x)

#digamma函数：计算给定参数的Ψ函数值（第一类对数勒让德函数）

digamma(x)

#digamma函数：计算给定参数的Ψ函数值（第一类对数勒让德函数）

trigamma(x)

#tetragamma函数：计算给定参数的Ψ函数的二阶导数值（第三类对数勒让德函数）

tetragamma(x)

#pentagamma函数：计算给定参数的Ψ函数的三阶导数值（第四类对数勒让德函数）

pentagamma(x)

#choose函数：计算组合数

choose(n,k)

#lchoose函数：计算组合数的自然对数

lchoose(n,k)

#fft函数：执行快速傅里叶变换（FFT），将信号从时域转换为频域。

fft(x)

#mvfft函数：执行多维傅里叶变换。

mvfft(x)

#convolve函数：计算两个向量的卷积（线性卷积）。

convolve(x, y)

#polyroot函数：找到多项式的根。

polyroot(p)

#polyroot函数：找到多项式的根。

poly(x,degree)

#spline函数：执行样条插值，生成平滑插值曲线。

spline(x, y, xout)

#splinefun函数：生成根据样条插值生成的函数。

splinefun(x,y)

参数 x：输入值。参数 nu：阶数。
#besselI函数：计算修正的贝塞尔函数I。

besselI(x, nu)

#besselK函数：计算修正的贝塞尔函数K。

besselK(x,nu)

#besselJ函数：计算贝塞尔函数J。

besselJ(x, nu)

#besselY函数：计算贝塞尔函数Y。

besselY(x, nu)

#gammaCody函数：计算递归修正伽玛函数。

gammaCody(x)

#deriv函数：对简单表达式进行符号微分或算法微分。

deriv(expr, name)

如有新学习的知识会补充，如有错误或遗漏请大佬们不吝赐教！！💖💖💖

1.+ - * / ^

2.%/%，%%和%*%

3.ceiling,floor,round

4.signif,trunc,zapsamll

5.max,min,mean,pmax,pmin

6.range和sum

7.prod

8.cumsum,cumprod,cummax,cummin

9.sort

10. approx

11.approx fun

12.diff

13.sign

14.var和sd

15.median

16.IQR

17.ave

18.fivenum

19.mad

20.quantile

21.stem

22.描述性统计函数

23.频数统计函数：先分组，在计算频数

24.独立性检验

25.相关性分析

26.相关性检验函数

27.偏度和峰度

28.一维优化与求根

29.常用数学函数

30.高级数学函数

知秋君

相关推荐