信号调制的三种方法

简介：

上节讲了调制中的调幅，其实就是控制高频振动信号的幅值；而调频也就是控制高频振动信号的频率；调相为控制高频振动信号的相位。总之，调制就是对载波信号的控制。

载波信号——高频振动信号

调频（FM)：

设基带信号为f(t),载波信号频率为 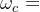$\omega _{c}$ ；则载波信号瞬时频率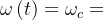 $\omega \left ( t \right )=\omega _{c}+k*f\left ( t \right )$
调频波的瞬时相位是瞬时频率从0-t的积分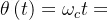： $\theta \left ( t \right )=\omega _{c}t+k*\int_{0}^{t}f\left ( t \right )dt$ ，后一项的最大值定义为调制指数

注：调频时，载波瞬时频率和基带信号成线性关系变化，同时瞬时相位和基带信号的积分成线性关系

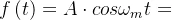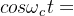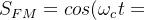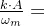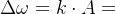若基带信号为 $f\left ( t \right )=A\cdot cos\omega _{m}t$ ,载波信号为 $cos\omega _{c}t$ ,利用上述两步可得调频后的信号 $S_{FM}= cos(\omega _{c} t+\frac{k\cdot A}{\omega _{m}}sin\omega _{m}t)$ 。其中调制指数m为 $\frac{k\cdot A}{\omega _{m}}$ ，最大频偏由第一步可知 $\Delta \omega =k\cdot A$ 。

调频波(FM)的最大频偏和基带信号频率无关，调制指数与基带信号频率成反比。

带宽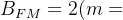： $B_{FM}=2(m+1)\omega _{m}$

若m<<1, 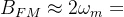$B_{FM}\approx 2\omega _{m}$ ,称为窄带调频(NBFM)

若m>>1, $B_{FM}\approx 2\Delta \omega$ ,称为宽带调频(WBFM)

简单示例：

载波信号为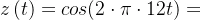 $z\left ( t \right )=cos(2\cdot \pi \cdot 12t)$ ,基带信号为 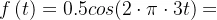$f\left ( t \right )=0.5cos(2\cdot \pi \cdot 3t)$ ,调频后信号为

import numpy as np
import scipy.fftpack as fftp
import matplotlib as mpl
import matplotlib.pyplot as plt
import scipy.signal as signalP
mpl.rcParams['font.sans-serif'] = ['KaiTi']   # 保证正常显示中文
mpl.rcParams['font.serif'] = ['KaiTi']        # 保证正常显示中文
mpl.rcParams['axes.unicode_minus'] = False    # 保证负号正常显示


dt = 0.001                                    # 时间域采样间隔
Fs = 1/dt                                     # 采样率
n = 1000
t = np.arange(dt, 5*n*dt+dt, dt)
N = 5*n

k = np.arange(N)
T = N/Fs
frq = k/T
frq1 = frq[range(int(N/2))]

plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.title('未调频基带信号')
y = 0.5*np.cos(2*np.pi*3*t)
plt.plot(t, y)
plt.xlabel('时间')
plt.ylabel('幅值')


plt.subplot(1,2,2)
plt.title('未调频基带信号频谱')
data_f = abs(np.fft.fft(y)) / N
data_f1 = data_f[range(int(N / 2))]
plt.plot(frq1, data_f1)
plt.xlim(0, 6)
plt.xlabel('频率')
plt.ylabel('幅值')
plt.show()

plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.title('调频后的信号')
f = np.cos(2*np.pi*12*t+0.5*np.sin(2*np.pi*3*t))
plt.plot(t, f)
plt.xlabel('时间')
plt.ylabel('幅值')


plt.subplot(1,2,2)
plt.title('调频后信号频谱')
data_ff = abs(np.fft.fft(f)) / N
data_f2 = data_ff[range(int(N / 2))]
plt.plot(frq1, data_f2)
plt.xlim(0, 20)
plt.xlabel('频率')
plt.ylabel('幅值')
plt.show()

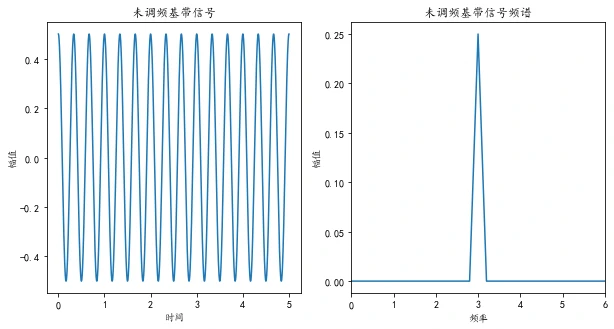
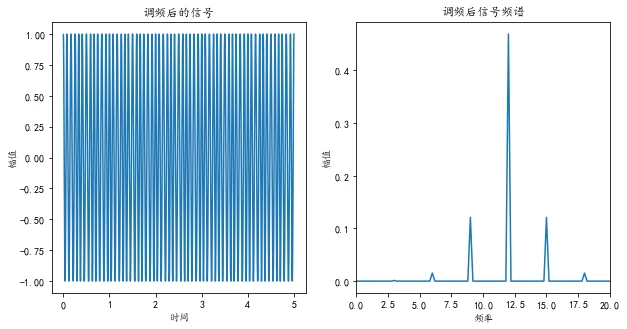
若其他不变，就基带信号幅值从0.5变为1。

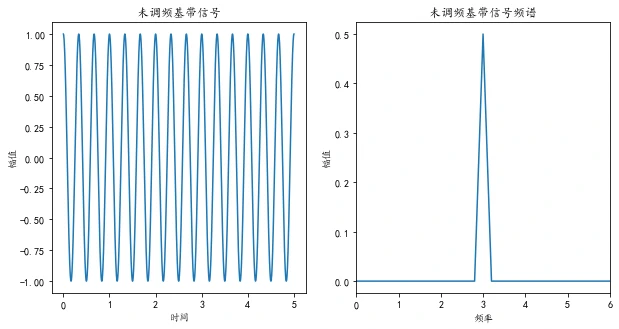
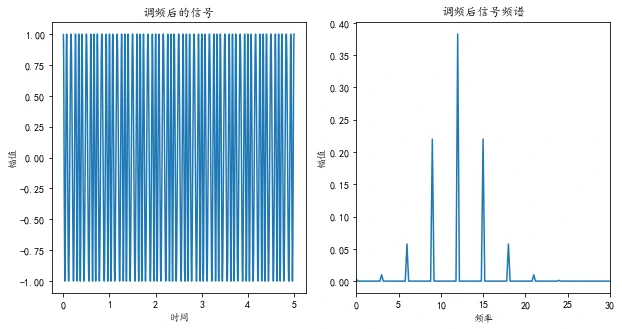
结论：调频信号的幅值越大，其频谱的幅值也越大，但频率值始终保持不变，幅值随着增大；

调频信号的幅值越大，经过调频之后的已调制信号的频谱越分散，边带包含的频率更多，且两两之间间隔为3hz。

FM正交解调：

FM正交解调就是将已调信号，通过乘上于其载波相同频率的正弦和余弦分量。然后通过低通滤波器，滤除二倍载波频率分量，保留下来的就是基带信号的正余弦形式。

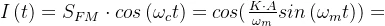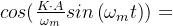$I\left ( t \right ) = S_{FM}\cdot cos\left (\omega _{c}t \right )=cos(\frac{K\cdot A}{\omega _{m}}sin\left ( \omega _{m}t \right ))+cos(2\omega _{c}t+\frac{K\cdot A}{\omega _{m}}sin\left ( \omega _{m}t \right ))$ ，就是余弦的和差公式，然后过滤掉2倍频就行， $cos(\frac{K\cdot A}{\omega _{m}}sin\left ( \omega _{m}t \right ))$ 。
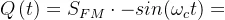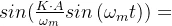同理 $Q\left ( t \right )=S_{FM}\cdot -sin(\omega _{c}t)$ 也会得到 $sin(\frac{K\cdot A}{\omega _{m}}sin\left ( \omega _{m}t \right ))$ 。
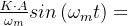再求Q(t)/I(t)的反正切，得到了 $\frac{K\cdot A}{\omega _{m}}sin\left ( \omega _{m}t \right )$ 。
再通过移相即可得到原始信号