一、概述
使用的书是来自机械工业出版社影印的《数学分析原理》,书号为ISBN 978-7-111-61954-3,对应于Walter Rudin的原书第三版。
作者在第一章提出了一个定理:
定理1.19:存在一个有序域R,它具备确界性质(least-upper-bound property)。特别地,R包含了有理数域Q。
定义了元素之间大小关系的集合,称为有序集;在有序集的基础上,定义加法和乘法的操作,使之符合加法乘法的公理(比如交换律等),便成为有序域,比如我们所熟知的实数域(这里的R其实就是指的实数域)。
确界性质,作者也给出了定义,即对于一个有序集而言,有上(下)界,就一定有上(下)确界。
作者将这个定理的证明放在了附录里,共分9个steps,从有理数域Q出发构造R。其中的Step 4个人感觉有错误:在Step 4的最后,证明 0 ∗ ⊂ α + β 0^\ast\subset\alpha + \beta 0∗⊂α+β时,作者用到了有理数域的阿基米德性。
错误的地方就在这里:作者在定理1.20里证明了实数域的阿基米德性,并且是建立在定理1.19成立的前提上,而在附录里证明1.19时,又用到了定理1.20。这是犯了循环论证的错误(用后面的东西,去证明前面的东西)

二、一些定义,以及证明的思路:
首先明确并回顾有理数集的分割(cut)的定义:
若集合 α \alpha α具有以下性质,则称之为有理数集Q的一个分割:
- α \alpha α是Q的非空真子集;
- 若 p ∈ α , q ∈ Q , 且 q < p , 则 q ∈ α p\in\alpha,q\in Q,且q<p,则q\in\alpha p∈α,q∈Q,且q<p,则q∈α;
- 若 p ∈ α , 则 ∃ r ∈ α , 使得 p < r p\in\alpha,则\exists r\in\alpha,使得p<r p∈α,则∃r∈α,使得p<r.
根据分割的定义,可以推出几条很有用的性质:分割内没有最大值(性质3);若p在分割内,则比p小的所有有理数都在分割内;若q不在分割内,那么比q大的所有有理数都不在分割内(性质2)。
2.1 分割在数轴上的表示
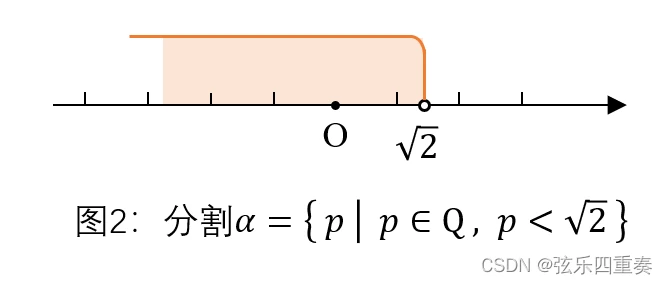
可以在数轴上来理解分割的数学意义:一个分割(cut)将实数轴分为左右两部分,虽然它是个有理数集,但在分界点处,既可以是有理数,也可以是无理数。如下图所示,它在 2 \sqrt{2} 2 处实现了分割 α \alpha α,但分割内的元素全部是有理数,且没有最大值,考虑数列:1,1.4,1.41,1.414,……,它们都是分割 α \alpha α 内的元素。
2.2 证明思路
证明中9个steps的逻辑概述如下:
- Step 1:提出分割(cut)的定义,以分割为元素构造出集合R。
- Step 2:在R集上定义有序,使之成为有序集。即定义两个分割之间的大小关系。
- Step 3:证明有序集R具有确界性质。
- Step 4, 5:在有序集R上定义加法。即定义两个分割之间相加的法则。
- Step 6, 7:在有序集R上定义乘法。即定义两个分割之间相乘的法则。(自此,有序集R变成了有序域,且具有确界性质)
- Step 8, 9:揭示并证明某些分割(cuts)与有理数(rational numbers)在算术与比较上的等价性,从而证明Q是R的一个子域。揭示不同的有序域之间的某种同构性,比如有理数域、实数域、复数域等等。
【注】对于命题 0 ∗ ⊂ α + β 0^\ast\subset\alpha + \beta 0∗⊂α+β. 其中:
- 0 ∗ 0^\ast 0∗ 指的是一个特殊的分割,它包含了所有的负有理数;
- α \alpha α指的是任意一个普通的分割;
- β \beta β 也是一个分割,与 α \alpha α 相关,由满足下列性质的所有数 p p p 构成: ∃ r > 0 , 使得 − p − r ∉ α . \exists r>0, 使得-p-r\notin\alpha. ∃r>0,使得−p−r∈/α.
- 两个分割的加法操作,被定义为 r + s r+s r+s 所能取到的所有值构成的集合,其中 r ∈ α , s ∈ β r\in\alpha,s\in\beta r∈α,s∈β.
综上这个命题可以改写为: ∀ v ∈ Q 且 v < 0 , ∃ p ∈ α , q ∈ β ,使得 v = p + q \forall v\in Q且v<0,\exists p\in\alpha,q\in\beta,使得v=p+q ∀v∈Q且v<0,∃p∈α,q∈β,使得v=p+q.
三、改进Step 4(讨论涉及到的所有数字,都是有理数)
在第四步中,证明 0 ∗ ⊂ α + β 0^\ast\subset\alpha + \beta 0∗⊂α+β 时,作者提供的证明如下:
Step 4:
……
为了证明 0 ∗ ⊂ α + β 0^\ast\subset\alpha + \beta 0∗⊂α+β,任选负有理数 v ∈ 0 ∗ v\in0^\ast v∈0∗,并使 w = − v / 2 w=-v/2 w=−v/2。于是有 w > 0 w>0 w>0,且存在整数 n n n 使得 n w ∈ α nw\in\alpha nw∈α 但是 ( n + 1 ) w ∉ α (n+1)w\notin\alpha (n+1)w∈/α(这一步是因为有理数域Q具有阿基米德性)。构造 p = − ( n + 2 ) w p=-(n+2)w p=−(n+2)w,于是 − p − w ∉ α -p-w\notin\alpha −p−w∈/α,从而有 p ∈ β p\in\beta p∈β,且: v = n w + p ∈ α + β . v=nw+p\in\alpha+\beta. v=nw+p∈α+β.于是得证 0 ∗ ⊂ α + β 0^\ast\subset\alpha + \beta 0∗⊂α+β.
因为可能会造成循环论证的原因,我们现在尝试不借助有理数域的阿基米德性,而使用更加原生的方法对其进行证明。
首先,我们先证明三个引理1,1x,2:
引理1:
∀ ε > 0 , ∃ p ∈ α ,使得 p + ε ∉ α . \forall\varepsilon>0,\exists p\in\alpha,使得p+\varepsilon\notin\alpha. ∀ε>0,∃p∈α,使得p+ε∈/α.
引理1的证明:
假设:存在某正有理数 ε 0 \varepsilon_0 ε0,使得对 α \alpha α 里的任意元素 p p p,均有 p + ε 0 ∈ α p+\varepsilon_0\in\alpha p+ε0∈α.
于是,有 p + 2 ε 0 ∈ α p+2\varepsilon_0\in\alpha p+2ε0∈α, p + 3 ε 0 ∈ α p+3\varepsilon_0\in\alpha p+3ε0∈α,…, p + k ε 0 ∈ α p+k\varepsilon_0\in\alpha p+kε0∈α,…(其中k为任意正整数).
同时,根据分割的性质2,比 p p p 小的有理数也全部属于 α \alpha α,即上式中 k k k 也可以取0和负整数.
对于 ∀ w ∈ Q \forall w\in Q ∀w∈Q,取 k = ⌈ w − p ε 0 ⌉ k=\lceil\frac{w-p}{\varepsilon_0}\rceil k=⌈ε0w−p⌉,则: w = p + ( w − p ) ≤ p + k ε 0 w=p+(w-p)\leq p+k\varepsilon_0 w=p+(w−p)≤p+kε0,由于 p + k ε 0 ∈ α p+k\varepsilon_0\in\alpha p+kε0∈α,故 w ∈ α w\in\alpha w∈α,即有理数集 Q ⊂ α Q\subset\alpha Q⊂α,这与分割的第一条性质相矛盾,因此假设不成立,引理1得证.
引理1x:(1x是对1的扩展)
∀ ε > 0 , ∃ p ∈ α ,使得下列两条性质成立 : 1 ) . p + ε ∉ α . 2 ) . ∃ r > 0 , 使得 p + ε − r ∉ α . \uad\uad\uad\uad\uad\uad\uad\uad\forall\varepsilon>0,\exists p\in\alpha,使得下列两条性质成立:\\\uad\uad\uad\uad\uad\uad\uad\uad\uad1).\quad p+\varepsilon\notin\alpha.\\\uad\uad\uad\uad\uad\uad\uad\uad\uad2).\quad\exists r>0,使得p+\varepsilon-r\notin\alpha. ∀ε>0,∃p∈α,使得下列两条性质成立:1).p+ε∈/α.2).∃r>0,使得p+ε−r∈/α.
引理1x的证明:
引理1证明了第一条性质,现证明性质2:
假设:存在某正有理数 ε 0 \varepsilon_0 ε0,使得对 α \alpha α 里的任意元素 p p p,和任意正有理数 r r r,均有 p + ε 0 − r ∈ α p+\varepsilon_0-r\in\alpha p+ε0−r∈α.
令 r = ε 0 / 2 r=\varepsilon_0/2 r=ε0/2,于是有 p + ε 0 / 2 ∈ α p+\varepsilon_0/2\in\alpha p+ε0/2∈α,同理 p + ε 0 / 2 + ε 0 − r p+\varepsilon_0/2+\varepsilon_0-r p+ε0/2+ε0−r 也属于 α \alpha α,即 p + ε 0 ∈ α p+\varepsilon_0\in\alpha p+ε0∈α.
也就是说,对 α \alpha α 里的任意元素 p p p,均有 p + ε 0 ∈ α p+\varepsilon_0\in\alpha p+ε0∈α. 这与性质1相矛盾,因此假设不成立,性质2成立,引理1x得证.【注解】
性质2给了这样的揭示:可选取 p p p 使得 p + ε p+\varepsilon p+ε 不是落在分割 α \alpha α 之外的最小元素,即:可以选取一个更小的 p p p 使得性质1成立;换句话说,对任意 ε > 0 \varepsilon>0 ε>0 至少可以选取两个不同的 p p p,使得性质1成立(事实上,可以选取无穷多个这样的 p p p,鉴于分割内没有最大值,但我们只需要两个就足够了)。至于是否存在一个最小的 p + ε p+\varepsilon p+ε,需要证明。从分割在数轴上的表示来看,可以清楚看到这个最小值应该是存在的,即分割点处,如果分割点是有理数的话。
引理2:
∀ ε > 0 , ∃ p ∈ α ,使得 − p − ε ∈ β . \forall\varepsilon>0,\exists p\in\alpha,使得-p-\varepsilon\in\beta. ∀ε>0,∃p∈α,使得−p−ε∈β.
引理2的证明:
根据有理数集 β \beta β 的定义,若要使 − p − ε ∈ β -p-\varepsilon\in\beta −p−ε∈β,需找到 r > 0 r>0 r>0,使得 p + ε − r ∉ α p+\varepsilon-r\notin\alpha p+ε−r∈/α. 这是引理1x的性质2的直接推论,故引理2得证。
最终命题:
现在,我们开始证明最终命题: 0 ∗ ⊂ α + β 0^\ast\subset\alpha + \beta 0∗⊂α+β.
试证: ∀ v ∈ 0 ∗ , ∃ p ∈ α , q ∈ β ,使得 v = p + q . \forall v\in0^\ast,\exists p\in\alpha,q\in\beta,使得v=p+q. ∀v∈0∗,∃p∈α,q∈β,使得v=p+q.
证明:
对于 ∀ v ∈ 0 ∗ \forall v\in0^\ast ∀v∈0∗,取 ε = − v \varepsilon=-v ε=−v,根据引理2,存在 p ∈ α p\in\alpha p∈α,使得 q = − p − ε ∈ β q=-p-\varepsilon\in\beta q=−p−ε∈β,且 p + q = − ε = v p+q=-\varepsilon=v p+q=−ε=v. 命题得证.
其实可以当做是引理2的直接推论了!
小结:
新的证明过程,摆脱了对有理数域的阿基米德性的依赖,填补了原步骤Step 4末尾环节的证明疏漏。
这是因为作者在证明阿基米德性(即定理1.20)时,用到了定理1.19,所以在证明1.19时最好不要再循环使用阿基米德性。
或许有人认为:在Step 3中,作者已经证明了有序集R具有确界性质,而定理1.20的证明过程用到的也是确界性质,所以Step 3之后就可以使用使用定理1.20了。
这种看法是错误的的!!!
因为在阿基米德性的定义中,既用到了有序性,也用到加法和乘法的操作,所以阿基米德性是有序域才会有的性质。Step 4的末尾,要用到有理数域Q的阿基米德性,有理数域也确实是有序域,但此时还没有任何一个定理能够证明Q具备确界性质,就更无法证明Q具备阿基米德性了。附录里9个steps做的事情,就是通过构造性的方式证明定理1.19:至少存在一个有序域,它具备确界性质。到step 4时,R还仅仅是个有序集。所以,直到step 9结束,我们才可以认为R是个具备确界性质的有序域,Q亦然。随后,定理1.20才能得证。
