

第三节:齐次方程
一、齐次方程
如果一阶微分方程可以写成以下形式:

那么就称这种方程为齐次方程。例如:

是齐次方程,因为它可以化为:

即:
𝑑𝑦𝑑𝑥=𝜙(𝑦𝑥).dxdy=ϕ(xy).
在齐次方程中,引入新的未知函数:

就可以将它化为可分离变量的方程。根据(3-2):

将这些代入方程(3-1)中,得到:

即:

分离变量,得到:
𝑑𝑢𝜙(𝑢)−𝑢=𝑑𝑥𝑥.ϕ(u)−udu=xdx.
两端积分,得到:

求出积分后,再以 𝑦𝑥xy 替代 𝑢u,便得到所给齐次方程的通解。
二、例子
例1: 解方程:

解: 原方程可以写成:

因此是齐次方程。令:

则:

于是原方程变为:

即:

分离变量,得:

两端积分,得:

计算积分并将结果表示成方程的通解。

二、可化为齐次的方程
有一些非齐次微分方程可以通过适当的变换化为齐次方程。例如,考虑方程:

当 𝑀M 和 𝑁N 中只包含齐次项时,这个方程就是齐次的。否则,它是非齐次的。对于非齐次的情形,可以使用下面的变换将其化为齐次方程:
令:

其中 ℎh 和 𝑘k 是待定的常数。那么:
代入方程(3-3),得:
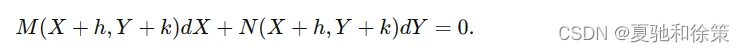
通过方程组确定 ℎh 和 𝑘k:

如果这个方程组的系数行列式不为零,则可以求得 ℎh 和 𝑘k,从而原方程(3-3)便化为齐次方程。
例3: 解方程:
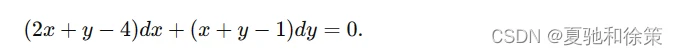
解: 所给方程属于(3-3)类型。令:

则:

代入原方程得:
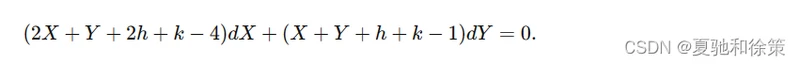
通过求解方程组:

得到:
ℎ=3,𝑘=−2.h=3,k=−2.
因此,令:
𝑥=𝑋+3,𝑦=𝑌−2,x=X+3,y=Y−2,
原方程变为:
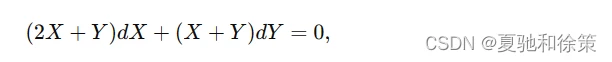
或:
𝑑𝑦𝑑𝑥=2𝑋+𝑌𝑋+𝑌.dxdy=X+Y2X+Y.
这是齐次方程。令:
𝑢=𝑌𝑋,u=XY,
则:
𝑌=𝑋𝑢,𝑑𝑦𝑑𝑥=𝑢+𝑋𝑑𝑢𝑑𝑥.Y=Xu,dxdy=u+Xdxdu.
将这些代入方程,得到:
𝑢+𝑋𝑑𝑢𝑑𝑥=2+𝑢1+𝑢.u+Xdxdu=1+u2+u.
即:

分离变量,得:

两端积分,得:

积分后可以得到方程的通解。






