
2022南京中考家长交流群QQ群:724824123
【学习目标】
1. 了解因式分解的意义,以及它与整式乘法的关系;
2.能确定多项式各项的公因式,会用提公因式法将多项式分解因式。
【要点梳理】
要点一、因式分解
把一个多项式化成几个整式积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
要点诠释:
(1)因式分解只针对多项式,而不是针对单项式,是对这个多项式的整体,而不是部分,因式分解的结果只能是整式的积的形式。
(2)要把一个多项式分解到每一个因式不能再分解为止。
(3)因式分解和整式乘法是互逆的运算,二者不能混淆.因式分解是一种恒等变形,而整式乘法是一种运算。
要点二、公因式
多项式的各项中都含有相同的因式,那么这个相同的因式就叫做公因式。
要点诠释:
(1)公因式必须是每一项中都含有的因式.
(2)公因式可以是一个数,也可以是一个字母,还可以是一个多项式.
(3)公因式的确定分为数字系数和字母两部分:①公因式的系数是各项系数的最大公约数.②字母是各项中相同的字母,指数取各字母指数最低的。
要点三、提公因式法

要点诠释:
(1)提公因式法分解因式实际上是逆用乘法分配律,
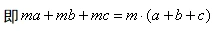
(2)用提公因式法分解因式的关键是准确找出多项式各项的公因式.
(3)当多项式第一项的系数是负数时,通常先提出“—”号,使括号内的第一项的系数变为正数,同时多项式的各项都要变号.
(4)用提公因式法分解因式时,若多项式的某项与公因式相等或它们的和为零,则提取公因式后,该项变为:“+1”或“-1”,不要把该项漏掉,或认为是0而出现错误.
【典型例题】
类型一、因式分解的概念
例1、下列由左到右的变形,哪些是因式分解?哪些不是?请说明理由.

【思路点拨】
根据因式分解的定义是将多项式形式变成几个整式的积的形式,从对象和结果两方面去判断.
解:因为(1)(2)的右边都不是积的形式,所以它们都不是因式分解;
(4)的左边不是多项式而是一个单项式,

只有(3)的左边是多项式,右边是整式的积的形式,所以只有(3)是因式分解.
【总结升华】
因式分解是将多项式变成积的形式,所以等式的左边必须是多项式,将单项式拆成几个单项式乘积的形式不能称为因式分解.等式的右边必须是整式因式积的形式.
举一反三:
【变式】下列变形是因式分解的是 ( )
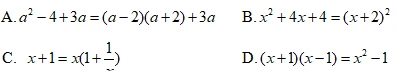
【答案】B;
类型二、提公因式法分解因式
例2、把下列各式分解因式:
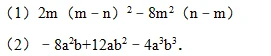
【思路点拨】
(1)直接提取公因式2m(m﹣n),进而分解因式得出答案;
(2)直接提取公因式﹣4ab,进而分解因式得出答案.
【答案与解析】

【总结升华】
此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.
举一反三:
【变式】下列分解因式结果正确的是( )

【答案】D.

类型三、提公因式法分解因式的应用
例3、若a、b、c为△abc的三边长,且(a-b)b+a(b-a)=a(c-a)+b(a-c),则△abc按边分类,应是什么三角形?
【答案与解析】

【总结升华】
将原式分解因式,就可以得出三边之间的关系,从而判定三角形的类型.

【答案与解析】

【总结升华】

举一反三:

【答案与解析】
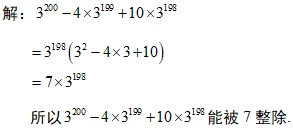
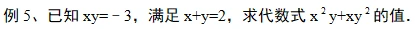
【思路点拨】
将原式提取公因式xy,进而将已知代入求出结果即可.
【答案与解析】

【总结升华】
此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键。


免责申明:本音频、视频和相关素材来源于网络。转载出于传递信息和学习之目的。如转载涉及版权等问题, 请立即联系管理员,我们会更改或删除相关文章,保证您的权利。
