目前，描述两个坐标系之间关系的常用方法主要有欧拉角法、方向余弦矩阵法和四元数法。因此要弄懂这三种方法的定义及关系，我们必须先从坐标系转化开始了解。下面以四旋翼为例，定义两个坐标系。导航坐标系(参考坐标系)n，选取东北天右手直角坐标系作为导航坐标系n、载体坐标系(机体坐标系)b，选取右手直角坐标系定义：四轴向右为X正方向，向前为Y轴正方向，向上为Z轴正方向。
欧拉角：欧拉角是一种常用的描述方位的方法，是由欧拉提出的。基本思想就是将两个坐标系的变换分解为绕三个不同的坐标轴的三次连续转动组成的序列。欧拉角的旋转规定为连续两次旋转，必须绕着不同的转动轴旋转，所以一共有12种旋转顺规。这里我们选用Z-Y-X的旋转顺规来描述b系与n系的关系。Z-Y-X顺规就是指。绕Z轴旋转偏航角(YAW)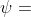
，绕Y轴旋转横滚角(ROLL)
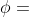，绕X轴旋转俯仰角(PITCH)
。
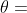先由简单的2维XY坐标系计算，如下图，载体坐标系b和导航坐标系n初始重合，绕X轴逆时针旋转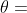角。向量OA在导航坐标系中的坐标为(Y,Z)，在载体坐标系中的坐标为(Y',Z')。则可以通过计算得出两个坐标的关系。
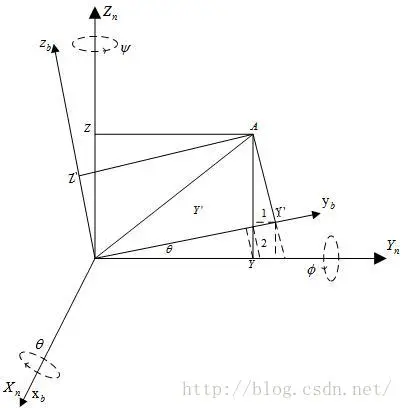
如上图，做出辅助线1可得 
写成矩阵运算为
,
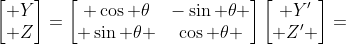推广至三维坐标系中则为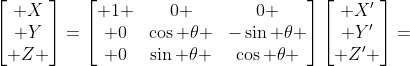
，
同理得绕Y轴旋转的坐标关系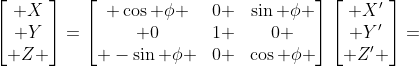
,
绕Z轴旋转的坐标关系为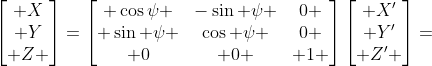
由此 得到经过三个欧拉角转动后，导航坐标系下的向量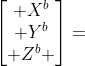
旋转后的与其对应的载体坐标系下的向量 
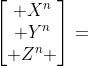之间的关系为，按Z-Y-X的顺规得到
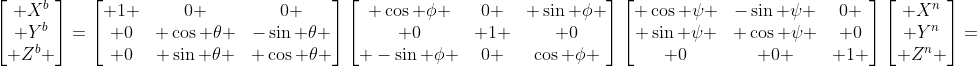
即为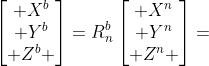
，其中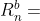
即为坐标系n到坐标系b的变换矩阵，我们平常定义的欧拉角形式的方向余弦矩阵为
，
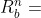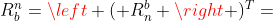
四元数：四元数是由四个元构成的数，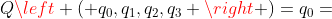
，其中，
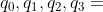是实数，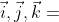
既是互相正交的单位向量，又是虚单位
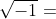。且满足以下四元数乘法关系：
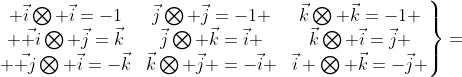
其中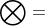
表示四元数乘法，具体展开为
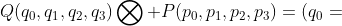
写成矩阵形式为
或者
其中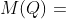
的构成形式为第一列是四元数
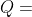本身，第一行是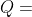的共轭四元数
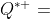的转置，剩下的部分是一个3行3列的矩阵
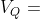称为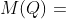的核，是由四元数构成的反对称矩阵
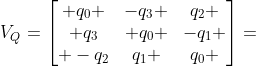
同理得到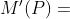
的核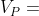
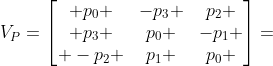
定义四元数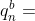
用来表示导航坐标系n到在台坐标系的旋转变换，那么有
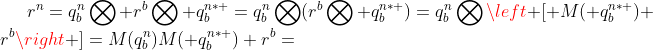
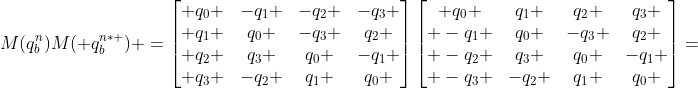
即为
其中
简化为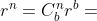
其中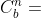
为通常定义的四元数旋转矩阵为载体坐标系b到导航坐标系n的旋转矩阵。
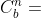四元数欧拉角、方向余弦矩阵之间的关系之间的关系，已知方向余弦矩阵和四元数旋转矩阵后，可以通过方向余弦矩阵的第一列和第三行元素计算姿态欧拉角如下
到此介绍完毕，欢迎大家互相交流指正。
