1.无穷大量的通俗理解是“要多大就有多大”,可分为正无穷大和负无穷大
2.无穷大量的充要条件是其倒数构成的数列是无穷小量
3.数列要与0保持一定的距离,才能使得它与无穷大量的乘积构成的新数列也是无穷大量
4.掌握关于无穷大量的Stolz定理及应用
我们继续数学基础的内容,这一次应该到“无穷大量”了。好了,废话不多说,进入正题。
上一期更新到:数列极限(二)

无穷大的定义
我们之前给出了无穷小量的定义——极限为0的变量,现在我们研究的是数列,所以这里提到的变量就是指数列。无穷小量的数列是收敛的,它的对立面自然而然想到的是无穷大,它是发散的,我们给出严格的定义:

与ε-N语言差不多,只不过这里是任意大,也即:要多大就有多大。我们看下面三个例子,分别对应正无穷大量,负无穷大量和无穷大量。
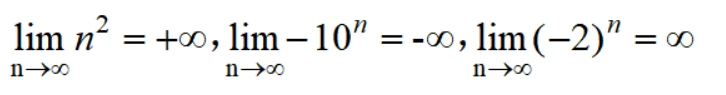
我们利用定义来证明两个例子是无穷大量。
例1

中括号“[ ]”表示整数部分,我们在映射与函数(二)
例2
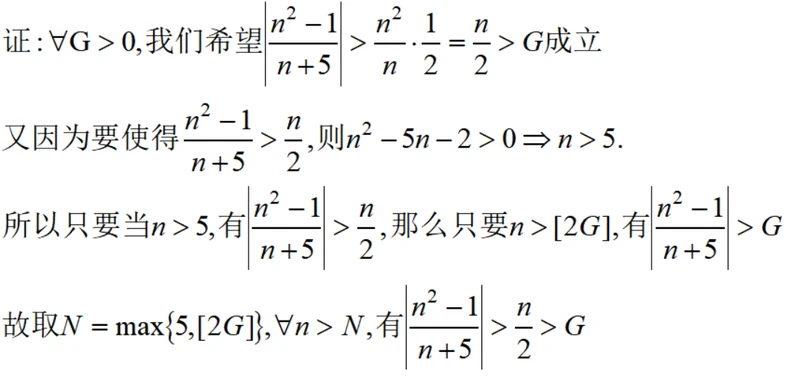
证明收敛常用的方法是放大法,这里证明无穷的方法刚好反过来——缩小法——比数列小的数列都要大于G,那么原数列必定大于G。这里唯一要说明的地方是如何缩小的,这里证明一步就把分子分母常数项去掉了,目的就是只剩余变量n,计算容易,但很显然相对原数列放大了,所以要缩小一倍再去寻找符合条件的n(这里只需要解抛物线即可,容易得到n>5)

与无穷大相关的定理
下面我们介绍无穷大量的相关定理,首先是最重要的一条定理:

若数列通项不为0,则数列是无穷大量的充要条件是其倒数构成的数列是无穷小量
直接利用定义法可以相互证明:

下面定理与推论叙述了无穷大量与其他数列乘积的关系:
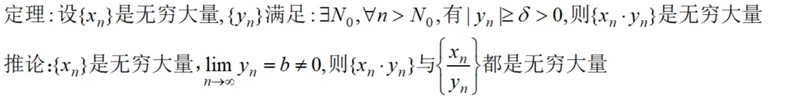
我们证明定理,推论根据数列保序性很容易证明。
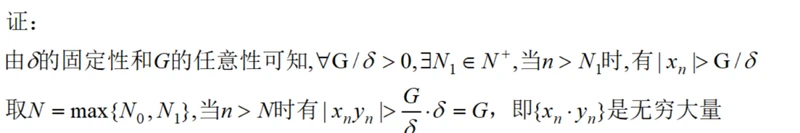
该定理表明,数列yn要与0保持一定的距离,才能使得它与无穷大量的乘积构成的新数列也是无穷大量.
根据该定理可以很简单求得一些极限,我们看下面一个例子:
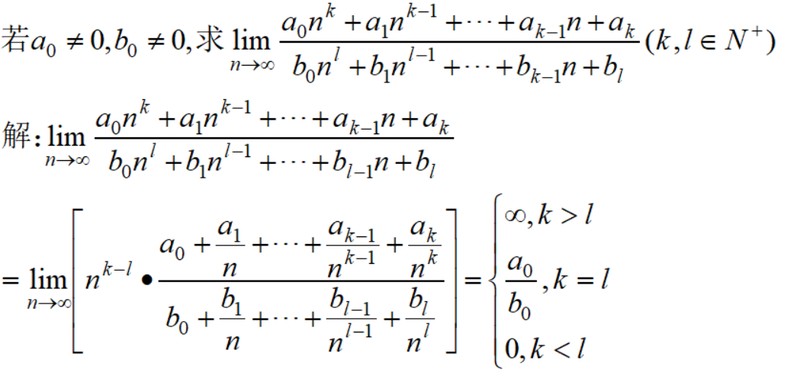
倒数第二个等号的中括号里,乘积有部分的极限是一个常数a0/b0,那么原极限就由乘积左部分唯一确定,当左部分是无穷大量,根据上面定理,原极限也是无穷大量,如果左部分是常数1,则原极限为a0/b0,如果左部分为0,根据极限四则运算,原极限为0
注:该结论用在下面stolz定理第一个例子里面

无穷大量的运算
关于无穷大量的运算,下面五条是唯一确定的:

除了上面五条,还有一些是无法确定的,需要具体问题具体分析,我们称为“待定型”极限(0表示无穷小量):
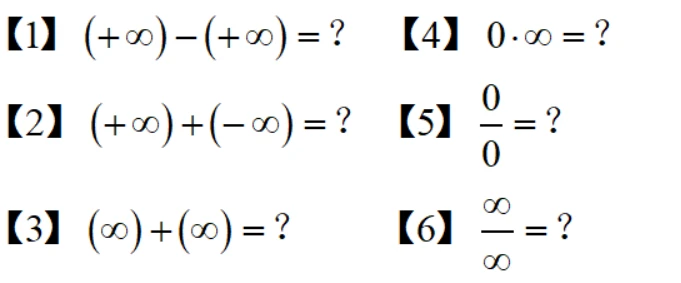
对于以上求极限问题,经常使用Stolz定理求解,下面介绍该定理:

其中单调数列定义如下:

我们证明该定理,先证明a为有限数(实数)的情况:

接着证明a为正无穷大的情况(负无穷大类似):
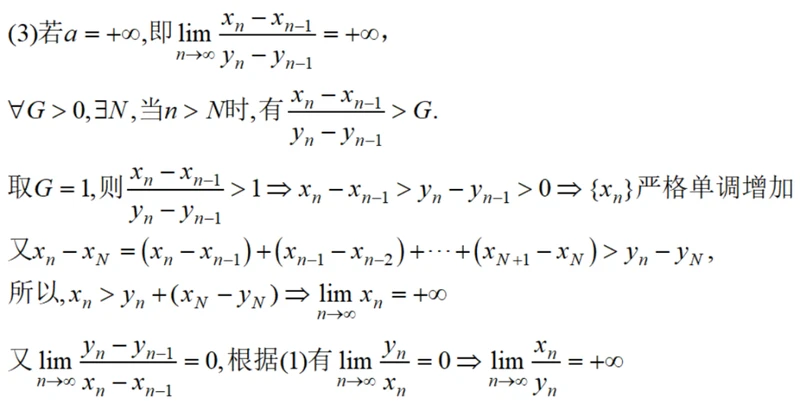
证明(3)情况直接用到(1)的结论,将xn与yn反过来,只要证明数列xn是严格增加且趋于正无穷即可。当然,用到了我们第一个提到的定理“无穷大量的倒数是无穷小量”。到这里你Get到了数学的思维火花吗。

Stolz定理的应用
下面举两个例子理解stolz定理。
例1

例2

