目录
一.十进制与二进制相互转化
1.十进制转二进制
①整数部分转化
②小数部分转化
2.二进制转十进制
二.十进制与八进制相互转化
1.十进制转八进制
①整数部分转换
②小数部分转换:
2.八进制转十进制
三.二进制与八进制相互转化
1.二进制转八进制
2.八进制转二进制
四.二进制与十六进制相互转化
1.二进制转十六进制
2.十六进制转二进制
五.八进制与十六进制相互转化
1.八进制转十六进制
2.十六进制转八进制
六.十进制与十六进制相互转化
1.十进制转十六进制
2.十六进制转十进制
一.十进制与二进制相互转化
1.十进制转二进制
①整数部分转化
“除2取余,逆序排列”
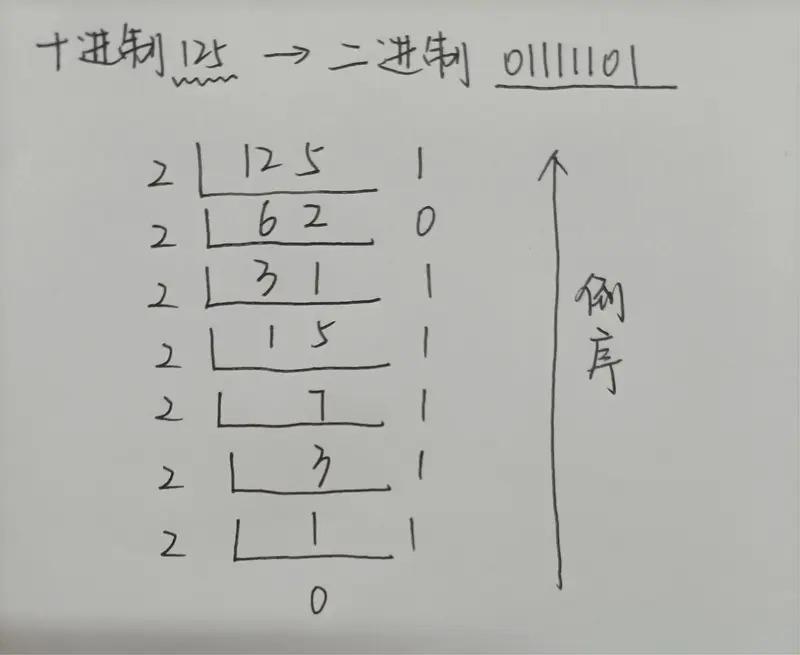
②小数部分转化

2.二进制转十进制
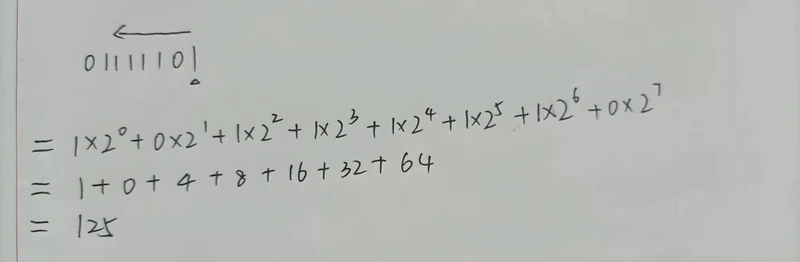
二.十进制与八进制相互转化
1.十进制转八进制
①整数部分转换

②小数部分转换:
小数部分乘以8,然后取整数部分,一直循环,直到小数不部分为零为止
如果小数部分永远也碰不到零,可以根据位数四舍五入或者保留循环部分

2.八进制转十进制

三.二进制与八进制相互转化
1.二进制转八进制
| 二进制数 | 八进制数 |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
方法:取三合一法,即从二进制的小数点为分界点,向左(向右)每三位取成一位,接着将这三位二进制按权相加,得到的数就是一位八位二进制数,然后,按顺序进行排列,小数点的位置不变,得到的数字就是我们所求的八进制数。如果向左(向右)取三位后,取到最高(最低)位时候,如果无法凑足三位,可以在小数点最左边(最右边),即整数的最高位(最低位)添0,凑足三位。
例:二进制数101110.101转换为八进制为 56.5
二进制数1101.1(相当于001101.100)转换为八进制为 15.4
2.八进制转二进制
方法:相当于反过来的二进制转八进制。
取一分三法,即将一位八进制数分解成三位二进制数,用三位二进制按权相加去凑这位八进制数,小数点位置照旧。
例:将八进制数56.5转换成二进制为 101110.101
将八进制数15.4转换成二进制为 001101.100 ,即1101.1
四.二进制与十六进制相互转化
| 第几位数 | 二进制 | 十六进制 |
| 1(1) | 0001 | 0x01 |
| 2(2) | 0010 | 0x02 |
| 3(3) | 0011 | 0x03 |
| 4(4) | 0100 | 0x04 |
| 5(5) | 0101 | 0x05 |
| 6(6) | 0110 | 0x06 |
| 7(7) | 0111 | 0x07 |
| 8(8) | 1000 | 0x08 |
| 9(9) | 1001 | 0x09 |
| 10(A) | 1010 | 0x0A |
| 11(B) | 1011 | 0x0B |
| 12(C) | 1100 | 0x0C |
| 13(D) | 1101 | 0x0D |
| 14(E) | 1110 | 0x0E |
| 15(F) | 1111 | 0x0F |
1.二进制转十六进制
取四合一法,即从二进制的小数点为分界点,向左(或向右)每四位取成一位,按照二进制与十六进制数的对应表,将每四位二进制对应的十六进制数按照顺序排列,小数点的位置不变,最后得到的就是十六进制数。如果取到最高位或最低位无法凑足四位,可以在最高位前面或最低位后面补零,再进行换算。
例:二进制数 101110011011.1001 转换为十六进制为 B9B.9
二进制数 10111.011 可补零为:00010111.0110 再转换为十六进制为 17.6
2.十六进制转二进制
将二进制转十六进制的转换规则反过来,取一分四法,即一个十六进制数分成以四个二进制数为一组,按照二进制与十六进制数的对应表进行替换,按顺序排列,小数点位置不变
例:十六进制为 B9B.9 转换为二进制数为101110011011.1001
五.八进制与十六进制相互转化
1.八进制转十六进制
①八进制转化成二进制,再从二进制转十六进制
②八进制转化成十进制,再从十进制转十六进制
2.十六进制转八进制
①十六进制转二进制,在从二进制转八进制
②十六进制转化成十进制,再从十进制转八进制
六.十进制与十六进制相互转化
1.十进制转十六进制
十进制数除16取余,直至商为0,与前面十进制转二进制八进制方法相似
2.十六进制转十进制
例:十六进制数 96 转化为十进制为 6*16^0+9*16^1=6+144=150
