原文教材 与 参考资料：

        Boneh Dan , Shoup Victor . A Graduate Course in Applied Cryptography[J].

        该书项目地址（可以免费获取）：http://toc.cryptobook.us/

        博客为对该书的学习笔记，并非原创知识，帮助理解，整理思路。
 

12.3 CCA-secure encryption from trapdoor function schemes

本节主要描述了一种基于陷门函数满足CCA安全的通用构造，在12.6节将展示如何将一个CPA方案转换为一个CCA方案的通用方法。在本节首先考虑使用一个基于陷门函数算法的公钥加密算法，以及一个哈希函数（作为随机谕言机），以及一个对称加密算法。由上述三个密码学原语构造一个加密方案如下：

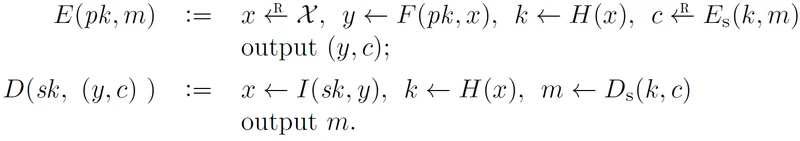
 这里需考虑一个问题：

       如果密文（y,c）是一个错误的密文，即为y没有一个F(pk，x)的原像，在现实中算法是可以拒绝错误密文的，此处，我们只需要修改一下解密算法，新的解密算法会在接收到密文请求后进行一次F函数的判断，如果y没有原像，意味着y不是一个由正确的私钥sk计算得到的部分密文，所以直接返回拒绝，具体的算法描述如下：

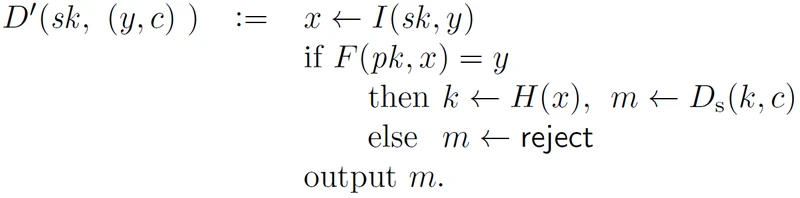
证明：如果H作为随机谕言机，对称加密算法是1CCA安全的，并且假设陷函数是单向的，那么上文所述加密算法是CCA安全的。特别的，如果接收到了一个错误的部分密文y, 那么还需要一个限制条件更强的假设，该陷门函数需要能够拒绝错误密文，所以，为陷门函数增加一个“原像谕言机”，该新的陷门假设如下：

值得注意的是，每一个单项陷门函数协议都可以比较容易的转换为一个IOW假设。

 安全定理：

       构造证明的结构与目的：如果存在一个敌手A能够攻击该方案，那么存在另外的敌手Biow和BS敌手能够通过调用A来攻击单向陷门假设和1CCA的对称加密方案。

       证明设计流程：为了达到上述证明的构造结构与目的，敌手在进行解密询问时，必须限制该敌手不能从中获得任何的有益于其挑战询问的信息。所以在解密构造时，我们必须要设计挑战者回复为不适用私钥sk进行解密。这个需求可以通过随机谕言机来实现，挑战者维护一张表格，当敌手进行密钥的随机谕言机询问时，选择一个随机数作为解密询问的密钥，规定挑战密文不能用来进行解密询问。

      随机谕言机请求回复：如果敌手在先前某个点x, 进行过随机谕言机询问，那么挑战者使用先前在x点询问产生的随机谕言机结果k, 进行解密。否则，如火的敌手先前没有进行随机谕言机的询问，而进行解密询问，那么挑战者和敌手都不会知道正确的解密密钥。然后，挑战者选取一个随机数，使用该随机数进行解密。这里挑战者需要使用额外的技术维护一致性，因为如果敌手下次对于该点进行随机谕言机询问，那么敌手需要将之前随机选的密钥返回给敌手，这样从敌手的角度来看，不论是先进行解密询问还是先进性随机谕言机询问，其询问的对于部分密文y的请求都是同样的密钥。

     挑战者回复半挑战密文的解密询问：我们在回复解密请求的时候，必须要考虑到如下的请求形式，即y使挑战密文的部分密文，但是c却不是挑战密文，就是说有y的那一半解密询问和挑战询问的那一半y是相等的。直觉上，在单向陷门函数存在的条件下，敌手是很难请求到真正的x在随机谕言机询问中，即使问到了随机谕言机回复一个随机的K。而从敌手的角度看k也应该是一个和随机值不可区分的。所以，该协议的CCA安全立即就服从了该方案中使用对称加密方案的1CCA安全性。

证明如下：

           我们证明定理12.2 在一个1CCA安全的比特猜测游戏模型下：

 首先，我们定义Game 0 是运行在敌手A和本算法挑战者之间的有个游戏，这个游戏时一个比特猜测版本的1CCA攻击游戏。接着修改挑战者获得Game 1. 在每个游戏中，b是由挑战者选取的随机比特，b`定义了敌手最后的猜测输出。Wj 定义了在游戏Game j中，猜测正确的情况。

Game 0：描述如下图所示：

挑战者必须回复随机谕言机请求，以及加密和解密请求。敌手可进行任意次的随机谕言机询问，以及任意次的解密询问，但是只能进行一次加密询问。回忆一下，除了直接访问随机谕言机，敌手还可间接的访问随机谕言机通过加密和解密请求，挑战者也是可以访问随机谕言机的。

      在初始化阶段，挑战者计算一些信息，包括生成公私钥对，选择随机的k 和 b, 这些的目的是为了运行加密请求，这些内容可以在敌手没有发出挑战明文时完成。为了便于证明，我们想要我们的挑战者尽可能的少使用私钥sk,在解密请求中（尽量不适用，防止敌手在解密询问时获取相关有意义的信息）。这个要求将通过一个非一般性的策略实现解密和随机谕言机请求。

      本文在此处使用了一个联合数组实现随机谕言机。首先使用一个Map1[y->k],用Map1来映射部分密文y与K之间的关系。规定在x询问的返回值为k. 然后使用另一个表格Pre【y->x】来跟踪询问请求与y之间的关系。Map通常生成除了Pre已经被定义过，因为挑战者也会访问随机谕言机，在解密请求时Map1也会被填充建立新的条目，但是此时Pre确没有。

       处理解密请求：如果部分密文y相等，则使用默认的k进行解密。否则，检测Map1中是否记录了此时询问的部分密文y,如果没有则给表项中添加一个随机的k值。如果y有原像并且Map1没有记录，那么意味着不论是挑战者还是敌手都没有先前询问过y的原像x。所以一个新的随机数k对应于随机询问x。特别的，如果敌手后去请求了随机谕言机在x处，那么将会使用相同的y进行回复。换句话说，在解密询问时如果发现之前没有记录过的y,那么挑战者一定要记录，并且维持一致性，当随机谕言机在某个时刻询问相同的x时，保持回复的一致性。如果y没有原像，那么即使分配了随机的k也没有意义。      下一步，挑战者测试y是否满足F，如果不满足则挑战者拒绝这个密文。如上图中调用函数Image(pk,sk,y)来确认y是否有原像。 最后，如果y符合F，那么挑战者使用Map1表格中分配的随机k, 进行解密。挑战者可以在不知道x的情况下实现这一点。即为，此时挑战者在只有y作为解密询问的情况下随机赋予了解密密钥k。在Game 0中的（1）处包含实现了，挑战者此时是知道秘密值x的。

Game 1：

     Game 1 和 0的区别在于，删除了上图中的（1）。定义Z为敌手在Game 1向随机谕言机请求x时的事件。Game1 和 Game 0执行的过程都是相同的，除了Z事件的发生，所以可以使用Difference Lemma. 我们得到下式：   

 如果事件Z发生了，那么在Game1结束时，我们可以从Pre【】中获取一个x，这个x就是y的原像。我们即可以使用敌手A去构造一个BIow敌手，这个BIow敌手可以攻破该方案的陷门函数在原像谕言机的帮助之下。  BIow首先作为敌手和其CIOW挑战者运行获取pk,y. 然后Biow使用这些信息作为A的挑战者，与A运行本加密方案的挑战游戏。此时，

      （1）并没有在本游戏中被明确使用（除了计算y），sk没有被使用(除了计算image function)。

      （2）Biow可以使用image oracle.(通过请求CIOW挑战者）

    在这个游戏结束时，如果y 在Pre的条目中，那么Biow输出该条目中的x,所以得到：

最终，在Game1中，k 仅仅被使用去加密挑战明文，与解密y相同时的解密询问。所以，敌手本质上是攻击1CCA的对称加密算法，很用调用A实现了一个1CCA的敌手攻击本方案所用的对称加密算法。所以得到如下:

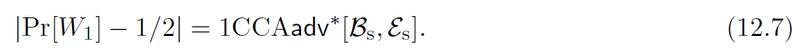
根据12.5 12.6. 12.7 我们可以获得12.4证明完毕。

12.4 CCA-secure EIGamal encryption

本书上节内容的基于TDF的加密方案可以使用任意的陷门函数实例化。在本节中主要探讨的是EIGamal协议的CCA安全性。回忆一下该方案的细节：

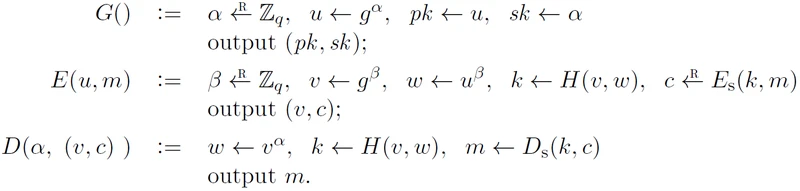然而，由CDH假设本身建立的这个方案并不是CCA安全的，敌手可以有效的借助解密询问来判断DH元组，敌手自己给出判断是非常困难的（DDH假设），解密请求可能会潜在的泄露私钥alpha的信息。虽然按照目前的知识来看，这种泄露并不会威胁到方案的安全性，然而，我们需要明确指出这种假设。所以，为了刻画这个模型，我们需要对CDH假设做出一定的修改，需要一个新的假设来捕获敌手的攻击行为，因为敌手的询问导致可以从解密谕言机获取一定的帮助，我们得到一个新的假设交互式CDH假设ICDH假设，描述如下：（即为在有DH判定谕言机的帮助下的CDH假设）

 进一步，我们得到如下安全定理：

安全定理：

 这个证明结构和上文的基于TDF的协议证明方式几乎没有什么区别，所以根据该书的内容，下文直接进行游戏描述，首先给出Game 0.

Game0 中：

             敌手的询问请求：

                （1）任意次的随机谕言机询问

                （2）任意次的解密询问

                （3）最多一次加密询问

                （4）可以通过加密与解密询问间接通过随机挑战者访问随机谕言机

           协议的初始阶段：

                 （1）挑战者生成公私钥对

                 （2）挑战者获取选取随机值k,b等加密询问参数，可以在不知道挑战明文时进行

          为了使挑战者尽可能少的使用密钥sk，需要采取类似TDF方案中处理的方式，设计随机谕言机回复避免使用私钥sk.

            随机谕言机的设计：

                Map[G2 -> k], 敌手提供(v,w) -> 得到k.

                Map1[G->k], u->k, 辅助记录.

                如果当且仅当（u,v,w）是一个DH元组，随机谕言机在(v,w)的点输出为k, 那么对于这个两个表而言Map[v,w] = Map1[v] = k. 在解密请求中，如果敌手发起的解密请求v, 并没有在随机谕言机中请求过，那么此处先行给Map1[v] 随机选择赋值k。 当敌手在后期如果再次询问到(v,w)时，继续将Map1中的k赋值给随机谕言机请求即可，保持一致性。

            随机谕言机请求：

            如果随机谕言机已经表格中已经存储了询问条目，那么直接返回结果，否则，按照如下的设计回复敌手：

            首先，测试敌手询问的是否是一个DH元组，使用函数DHP（*,*,*），同时这里也是唯一使用私钥的地方。

            如果这是一个DH元组，那么挑战者给Map1一个随机的值，如果Map1中没有定义的话，并进一步将这个随机值k赋值给Map。并且记录一个条目sol.  Sol 是另外一个辅助谕言机记录表格，用来记录ICDH实例。

            如果这不是一个DH元组，那么挑战者给与Map设定一个随机的值k, 这里并没有进一步设置Map1。

           解密请求回复：

           当挑战者收到一个解密请求（v,c）时，按照如下步骤处理：

          （1）如果部分密文v等于初始化阶段生成的v. 那么直接使用预先准备好的密钥进行解密。

          （2）如果不满足（1），那么检车是否满足在Map1中记录有，如果没有那么给与随机赋值k, 然后使用该随机的k作为密钥进行解密。显然，挑战者在回复解密请求的时候并没有使用CDH问题实例（u, v, w）的信息。然而如果敌手请求随机谕言机在这个实例(v,*)时刻，敌手将会看到同样的k,所以一致性得到了维护。

 Game 1 ： 

           Game 1 与 Game 0 一样的，除了（1）被删除了。定义Z为敌手A在Game1中请求（v,w），不难看出在Z不发生时两个游戏的运行过程是一样的。

            如果Z发生，那么在游戏的最后，我们从Sol中就可以获得w ,即为一个ICDH问题解的实例。我们可以调用A构造一个BICDH敌手去攻破CDH假设在有DH判断谕言机的帮助下，其优势等同于Z事件发生的概率。

考虑到和TDF一样的情形，我们类似得到可以调用A去攻击对称加密方案，最后得到上述两个等式，得证。