最近开始听MIT 18.01单变量微积分来复习微积分课程,听到第23讲的时候(对应的讲义可以到MIT opencourseware下载,讲义索引是session 65a),这节课我居然看到了关于概率分布函数的一些讲解,醍醐灌顶,可能我已经忘了大一都学了什么。想借这篇文章开始整理下高斯分布的一些知识。
本文内容对应我的博客中微积分笔记总目录下的第四章,积分应用中的概率求解。
背景问题
首先,在这节课当中,David Jerison教授用投掷飞镖的应用问题引出了类似于标准正态分布的曲线。具体问题是:你和你younger brother玩飞镖比赛,在你扔飞镖的时候有多大的可能性会误伤到站在飞镖盘附近的他?如图:
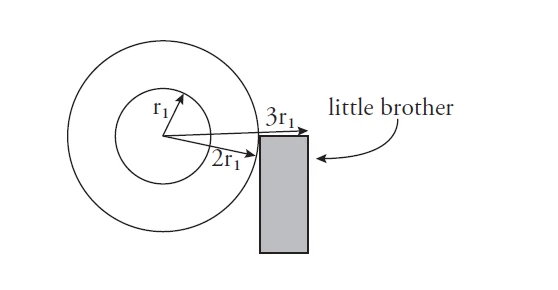
我们需要通过一些数学假设把这个文字问题来转化为具体的数学问题。首先,brother所在区域可以想象成是被一个更大的圆所包围的子区域,之后教授给出了单位面积内所有落点的次数随半径变化的函数(比如说有1000次掷飞镖的实验,落点就是指这些飞镖扎在某一半径内的盘子上的次数)
Number of hits per unit area = c e − r 2 ce^{-r^{2}} ce−r2 (跟标准正态分布函数只差一个参数)
由于飞镖落点不是均匀分布的,所以我们不能直接用younger brother所在区域的面积与整个圆的比值作为概率结果,而是要把上面的整个大圆平铺到X-Y平面作为基底,高度Z轴是
c
e
−
r
2
ce^{-r^{2}}
ce−r2这这样一来就等价于将整个钟形曲线以竖直轴旋转一圈(这里类似于求一个钟形的体积,但实际上更像是一个加权和)
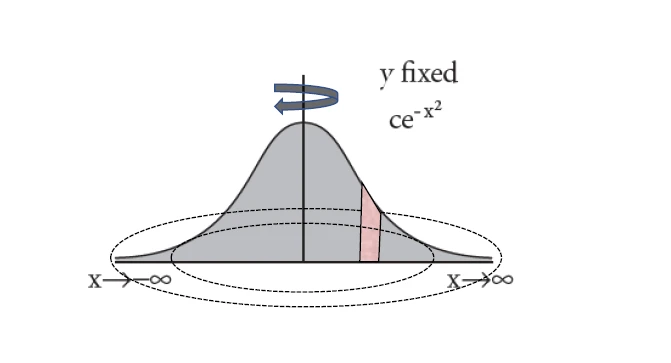
那么,飞镖落在圆环r1到r2之间的概率就是:(用壳层shell法求解)
P
(
p
a
r
t
)
=
P
(
r
1
<
r
<
r
2
)
=
c
∫
r
1
r
2
(
2
π
r
)
e
−
r
2
d
r
P(part)=P(r_1<r<r_2)=c\int_{r_1}^{r_2}(2\pi r)e^{-r^{2}}dr
P(part)=P(r1<r<r2)=c∫r1r2(2πr)e−r2dr
P
(
p
a
r
t
)
=
−
c
π
e
−
r
2
∣
r
1
r
2
=
−
c
π
(
e
r
2
−
e
r
1
)
P(part)=-c\pi e^{-r^2}\vert _{r_1}^{r_2}=-c\pi (e^{r_2}-e^{r_1})
P(part)=−cπe−r2∣r1r2=−cπ(er2−er1)
(其中 2 π r 2\pi r 2πr是底面周长, c e − r 2 ce^{-r^{2}} ce−r2是高度, d r dr dr是壳层厚度)
而整个钟形的体积为:
P
(
w
h
o
l
e
)
=
c
∫
0
∞
(
2
π
r
)
e
−
r
2
d
r
P(whole)=c\int_{0}^{\infty}(2\pi r)e^{-r^{2}}dr
P(whole)=c∫0∞(2πr)e−r2dr
P
(
w
h
o
l
e
)
=
−
c
π
e
−
r
2
∣
0
∞
=
−
c
π
(
e
∞
−
e
0
)
=
c
π
P(whole)=-c\pi e^{-r^2}\vert _{0}^{\infty}=-c\pi (e^{\infty}-e^{0})=c\pi
P(whole)=−cπe−r2∣0∞=−cπ(e∞−e0)=cπ
(这里是从0到
∞
\infty
∞而不是从
−
∞
-\infty
−∞到
∞
\infty
∞是因为旋转只需要一半的曲线就够了)
最后, P ( h u r t ) = P ( p a r t ) P ( w h o l e ) P(hurt)=\frac{P(part)}{P(whole)} P(hurt)=P(whole)P(part)
我觉得这个问题实际上讲出了类似于多变量连续函数的概率分布函数的应用,实际上概率密度函数曲线包围的面积就相当于在这个问题中把底层的二维圆形换成一维直线或线段。(终于解开了我在学概率论的时候对概率密度函数的困惑)
钟形函数(Bell Curve)的积分
首先从前面的背景问题中得知:
V
=
∫
0
∞
(
2
π
r
)
e
−
r
2
d
r
=
−
π
e
−
r
2
∣
0
∞
=
π
V=\int_{0}^{\infty}(2\pi r)e^{-r^{2}}dr=-\pi e^{-r^2}\vert _{0}^{\infty}=\pi
V=∫0∞(2πr)e−r2dr=−πe−r2∣0∞=π
这一部分我们将关注的是:
Q
=
∫
−
∞
∞
e
−
r
2
d
r
Q=\int_{-\infty}^{\infty}e^{-r^{2}}dr
Q=∫−∞∞e−r2dr
背景问题中,我们采用的方法是叠加每一层shell得到总体积,现在我们从另一个角度来看上面的图像,竖直方向一刀刀切开,得到
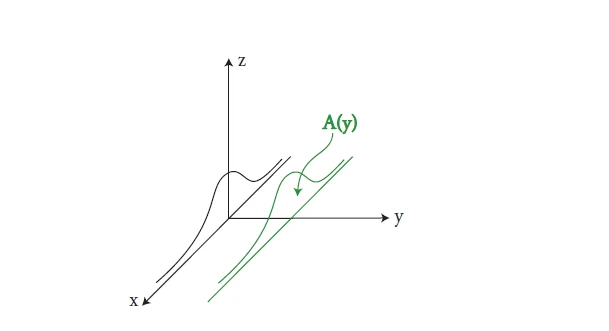
当y轴固定的时候(如下图),即
y
=
b
y=b
y=b时,
A
(
b
)
=
∫
−
∞
∞
e
−
r
2
d
r
=
∫
−
∞
∞
e
−
(
b
2
+
x
2
)
d
x
=
e
−
b
2
∫
−
∞
∞
e
−
x
2
d
x
=
e
−
b
2
Q
A(b)=\int_{-\infty}^{\infty}e^{-r^{2}}dr=\int_{-\infty}^{\infty}e^{-(b^{2}+x^2)}dx=e^{-b^2}\int_{-\infty}^{\infty}e^{-x^2}dx=e^{-b^2}Q
A(b)=∫−∞∞e−r2dr=∫−∞∞e−(b2+x2)dx=e−b2∫−∞∞e−x2dx=e−b2Q
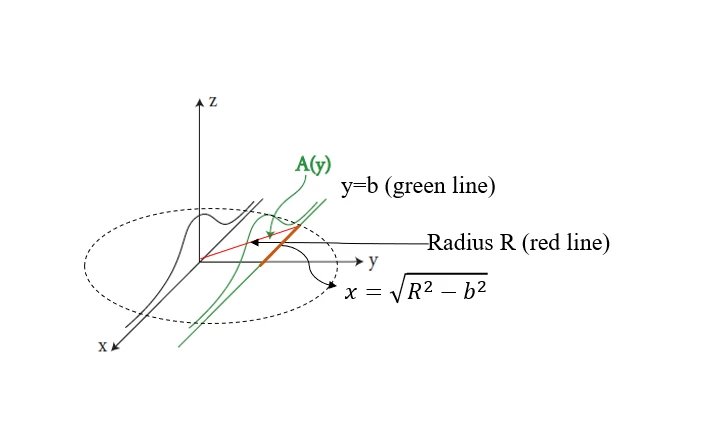
由于
V
=
∫
−
∞
∞
A
(
y
)
d
y
=
∫
−
∞
∞
e
−
y
2
Q
d
y
=
Q
∫
−
∞
∞
e
−
y
2
d
y
=
Q
2
=
V
V=\int_{-\infty}^{\infty}A(y)dy=\int_{-\infty}^{\infty}e^{-y^2}Qdy=Q\int_{-\infty}^{\infty}e^{-y^2}dy=Q^2=V
V=∫−∞∞A(y)dy=∫−∞∞e−y2Qdy=Q∫−∞∞e−y2dy=Q2=V
又因为我们知道
V
=
π
V=\pi
V=π,顺理成章,
Q
=
π
Q=\sqrt{\pi}
Q=π
这时再看看式子
Q
π
=
1
π
∫
−
∞
∞
e
−
x
2
d
x
=
1
\frac{Q}{\sqrt{\pi}}=\frac{1}{\sqrt{\pi}}\int_{-\infty}^{\infty}e^{-x^2}dx=1
πQ=π1∫−∞∞e−x2dx=1满足了全概率为1的最基本条件。
拉伸一下x轴,就可以得到标准正态分布概率密度的函数表达式。
通过换元法,
u
=
2
x
u=\sqrt{2}x
u=2x,
d
u
=
2
d
x
du=\sqrt{2}dx
du=2dx
可以得到:
1
2
π
∫
−
∞
∞
e
−
u
2
2
d
u
=
1
\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-\frac{u^2}{2}}du=1
2π1∫−∞∞e−2u2du=1(
2
\sqrt{2}
2被提了出来!)
标准正态分布的表达式就为
f
(
x
)
=
1
2
π
e
x
p
(
−
x
2
2
)
f(x)=\frac{1}{\sqrt{2\pi}}exp(-\frac{x^2}{2})
f(x)=2π1exp(−2x2)同理对称轴的移动和曲线的压缩与拉伸形成了均值为
μ
\mu
μ, 标准差为
σ
\sigma
σ的一维正态分布:
f
(
x
)
=
1
2
π
σ
e
x
p
(
−
(
x
−
μ
)
2
2
σ
2
)
f(x)=\frac{1}{\sqrt{2\pi}\sigma}exp({-\frac{(x-\mu)^2}{2\sigma^2}})
f(x)=2πσ1exp(−2σ2(x−μ)2)
这里我需要提醒自己之前犯的小错误:一开始把V的数值错误当成了 2 π 2\pi 2π,其实是多算了一倍,因为旋转只需要一半的曲线就够了。
