这是一种基于元学习的小样本学习方法,所以学习MAML首先要了解一下元学习、小样本学习的相关内容,可以参考https://blog.csdn.net/whscheetah/article/details/107993287 ,或者从其他渠道了解一些相关知识。
论文名称《Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks》,下载链接https://arxiv.org/abs/1703.03400

这个算法在表现形式上非常简单,但是解释起来比较困难。
这个算法的目的是采用元学习的方式获取到一个优秀的初始化参数 θ 。这个 θ 能适用于各种任务task。
很明显,MAML的优化过程分为两层:
1.内层循环:当前的参数是θ,输入的是 T 个任务的 training 集,每个任务都在 θ 的基础上,独立的进行一次梯度更新,得到 T 个优化后的结果,记作θ1,θ2,……θT。在高维空间里面,可以用图中的点形象的地表示。但是这 T 个 θi 好不好呢?显然不好,因为 θi 是由 任务 Ti 中的 training set 学习到的,适用于任务 Ti ,它只是它对应的任务 Ti 的最优解,而不是多个任务的最优解。
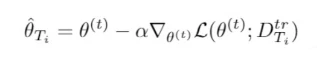
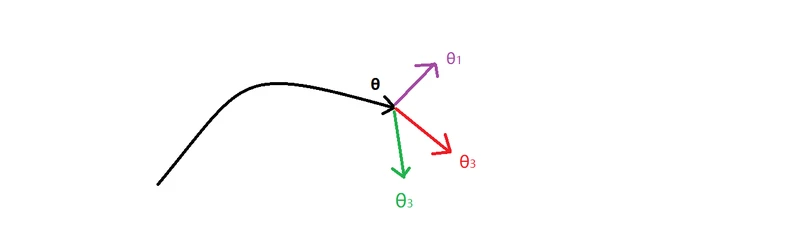
2.外层循环:那如何得到多个任务的最优解呢?总不能将这T个 θi 做个平均吧!因此,非常自然的想法就是,通过学习,获取适合多个任务的最优解。这就是以这 T 个 θi 为参数,在 test set 的基础上,进行再一次学习。
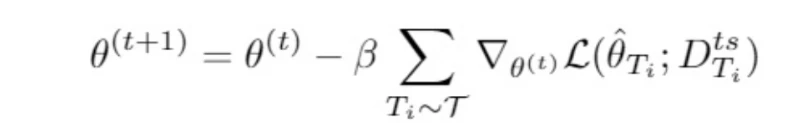
这次梯度下降的意义很明显,就是希望能获取一个 θ ,它能够使得 test set 在 T 个任务上的损失之和最小,这样得到的 θ ,显然就是能够适用于所有任务的最优解。
