最基础最重要的概念——叉积,说到叉积就要聊聊行列式。
行列式的代数意义与Cramer法则联系密切,先来个简单的例子,
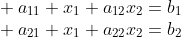
消除x2得到这样的结果:
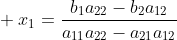
. 行列式

正是那个分母,其计算和叉积一样。
行列式的几何意义更加丰富,面积,体积……如上面的那个行列式就是向量为
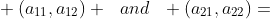
的叉积。也就是他们构成的平面的有向面积。
推广到三阶就是在x,y,z轴向量方向上的有向体积。


故在三维空间中,向量
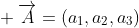
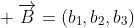
的叉积应该是(参照上图)。几何意义是对应平面
最基础最重要的概念——叉积,说到叉积就要聊聊行列式。 行列式的代数意义与Cramer法则联系密切,先来个简单的例子, 消除x2得到这样的结果: . 行列式 正是那个分母,其计算和叉积一样。 行列式的几何意义更加丰富,面积,体积……如上面的那个行列式就是向量为 的叉积。也就是他们构成的平面的有向面积。 推广到三阶就是在x,y,z轴向量方向上的有向体积。 故在三维空间中,向量
最基础最重要的概念——叉积,说到叉积就要聊聊行列式。
行列式的代数意义与Cramer法则联系密切,先来个简单的例子,
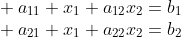
消除x2得到这样的结果:
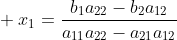
. 行列式

正是那个分母,其计算和叉积一样。
行列式的几何意义更加丰富,面积,体积……如上面的那个行列式就是向量为
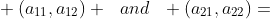
的叉积。也就是他们构成的平面的有向面积。
推广到三阶就是在x,y,z轴向量方向上的有向体积。


故在三维空间中,向量
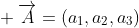
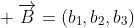
的叉积应该是(参照上图)。几何意义是对应平面