拓扑排序指的是有向无环图(DAG),「拓扑排序」是专门应用于有向图的算法。
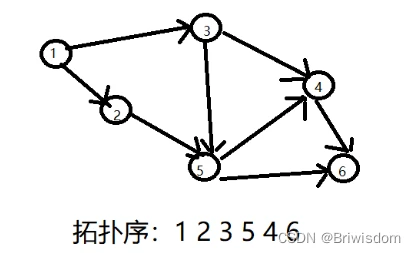
下面就是一个拓扑结构;
拓扑序就是,图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前
我们可以发现拓扑序不是唯一的;
接下来,我们需要知道一个概念——度:
对于有向图的某个结点来说,我们把指向它的边的数量叫做入度;
把从它发出的边的数量称为出度
拓扑序的问题有两个条件:不存在环,有向。
题目:
这道题用 BFS 和 DFS 都可以完成,BFS 的写法很经典,BFS 的写法就叫「拓扑排序」,这里还用到了贪心算法的思想,贪的点是:当前让入度为 0 的那些结点入队。
BFS的代码思路:
BFS表示广度优先遍历,即每次把节点的邻居都访问完了,再继续访问下一层的节点。使用了队列存储节点的顺序。
1)首先遍历得到每个节点的入度数,以及有向图的字典,即每个节点课程结束后,哪些课程可以继续执行的字典映射。比如,节点1,2,依赖节点0的执行,所以在字典中{ 0: [1,2] }
2)然后建立一个队列,队列具有先进先出的特点,先把入度为0的点,加进队列中。表示这些节点的课可以先修完,他们不依赖其它课程。
3)最后,建立队列的循环,每次出一个节点,知道所有入度为0的节点都出来了,队列为空退出循环,此时队列一次出来的节点顺序就是所求答案。
class Solution:
def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
if len(prerequisites)==0:
return list(range(numCourses))
in_degree=[0]*numCourses
adj=[set() for _ in range(numCourses)]
for s, f in prerequisites:
in_degree[s]+=1
adj[f].add(s)
queue=[]
res=[]
for i in range(numCourses):
if in_degree[i]==0:
queue.append(i)
while len(queue)>0:
cur=queue.pop(0)
res.append(cur)
for succe in adj[cur]:
in_degree[succe]-=1
if in_degree[succe]==0:
queue.append(succe)
if len(res)!=numCourses:
return []
return resDFS的代码思路:
DFS表示深度优先遍历。指遍历节点的一条路径到底,由图的低部向上回溯,中间的节点通过栈的结构存储,先进后出即为所求答案。
1)遍历每个节点,同样先建立每个节点的依赖关系字典结构。
2)建立有n个节点的visited数组,记录每个节点是否在访问,访问中,访问结束。以及是否有环的标记hasCycle。有环的情况下,无法输出拓扑排序。
3)写dfs函数,传入当前的节点。把该节点的visited标记为1,表示正在访问。
如果依赖字典中不存在该节点,则可以直接标记visited=2,表示已经访问过,stack 压入该节点。
否则遍历每一个依赖该节点的邻居节点,
- 如果visited[node]=0,表示未访问过,递归将该节点进入dfs函数,结束后判断是否hasCycle=True,如果是则遇到环,退出函数。
- 如果visited[node]=1表示正在访问中又进入了,则存在环hasCycle=True, 退出函数。
最后,将visited[node]=2,表示进入dfs的这个节点已经访问过了,避免重复访问,并把该节点压入stack栈。
4) 依次遍历每个节点,如果visited[node]==0则进入dfs函数。最后将stack依次弹出,即为所求答案。栈的弹出对于list来说,就是把每个数反着输出。
如果hasCycle=True,则有环,没有拓扑顺序。
class Solution:
def findOrder(self, numCourses: int, prerequisites):
def dfs(s):
nonlocal hasCycle
visited[s]=1
if s in graph:
for v in graph[s]:
if visited[v]==0:
dfs(v)
if hasCycle:
return
elif visited[v]==1:
hasCycle=True
return
visited[s]=2
stack.append(s)
return
visited=[0]*numCourses
hasCycle=False
graph={}
stack=[]
for s,f in prerequisites:
if f not in graph:
graph[f]=[s]
else:
graph[f].append(s)
for i in range(numCourses):
if visited[i]==0 and not hasCycle:
dfs(i)
return stack[::-1] if not hasCycle else []复习一下C++的BFS实现:
class Solution {
private:
vector <int> in_degree;
vector <int> result;
vector <vector <int>> edges;
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
in_degree.resize(numCourses);
for (const auto& info: prerequisites){
edges[info[1]].push_back(info[0]);
++in_degree[info[0]];
}
queue<int> q;
for(int i=0;i<numCourses;++i){
if (in_degree[i]==0){
q.push(i);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
result.push_back(u);
for(int v:edges[u]){
--in_degree[v];
if (in_degree[v]==0){
q.push(v);
}
}
}
if (result.size() !=numCourses){
return {};
}
return result;
}
};