中心极限定理概率表

概率基础——中心极限定理

引言

中心极限定理是概率论中的一个重要定理，它描述了在一定条件下，独立随机变量的均值经过适当标准化后，当样本容量足够大时，其分布将趋近于正态分布。中心极限定理在统计学和实践中具有广泛的应用，尤其是在推断统计学中。

中心极限定理的表述

中心极限定理可以表述为：对于具有有限方差的独立同分布随机变量 $X_1, X_2, ..., X_n$ ，它们的均值 $\bar{X}$ 的分布在 $n$ 足够大时，将近似服从正态分布，即：

$\lim_{n \to \infty} P\left(\frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \leq x\right) = \Phi(x)$

其中， $\mu$ 是随机变量 $X_i$ 的均值， $\sigma$ 是随机变量 $X_i$ 的标准差， $\Phi(x)$ 是标准正态分布的累积分布函数。

推导过程

我们可以通过特征函数的方法来推导中心极限定理。特征函数是随机变量的唯一标识，其定义为：

$\phi(t) = E(e^{itX})$

其中， $i$ 是虚数单位。

对于独立同分布的随机变量 $X_1, X_2, ..., X_n$ ，它们的均值为 $\mu$ ，方差为 $\sigma^2$ ，则其特征函数为：

$\phi_{\bar{X}}(t) = \phi_{X_1}(t) \phi_{X_2}(t) ... \phi_{X_n}(t) = [\phi(t)]^n$

通过特征函数的逆变换，我们可以得到样本均值 $\bar{X}$ 的分布。当 $n$ 足够大时，可以近似为正态分布。

中心极限定理模拟

从一个服从参数p=0.3的几何分布中进行采样，共分3组试验，每次分别采样2个、5个、50个样本，各重复100,000次，然后进行标准化。得到3组试验对应的结果。

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as geom

fig, ax = plt.subplots(2, 2)

geom_rv = geom.geom(p=0.3)
geom_rvs = geom_rv.rvs(size=1000000)

mean, var, skew, kurt = geom_rv.stats(moments='mvsk')
ax[0, 0].hist(geom_rvs, bins=50, density=True, alpha=0.5)
ax[0, 0].set_title('Geometric distribution')
ax[0, 0].grid(ls='--')
n_array = [0, 2, 5, 50]

for i in range(1, 4):
    Z_array = []
    n = n_array[i]
    for j in range(100000):
        sample = np.random.choice(geom_rvs, n)
        Z_array.append((sum(sample) - n * mean) / np.sqrt(var * n))
    
    ax[i // 2, i % 2].hist(Z_array, bins=100, density=True, alpha=0.5)  
    ax[i // 2, i % 2].set_title(f'n={n}')
    ax[i // 2, i % 2].set_xlim(-3, 3)
    ax[i // 2, i % 2].grid(ls='--')

plt.tight_layout()
plt.show()

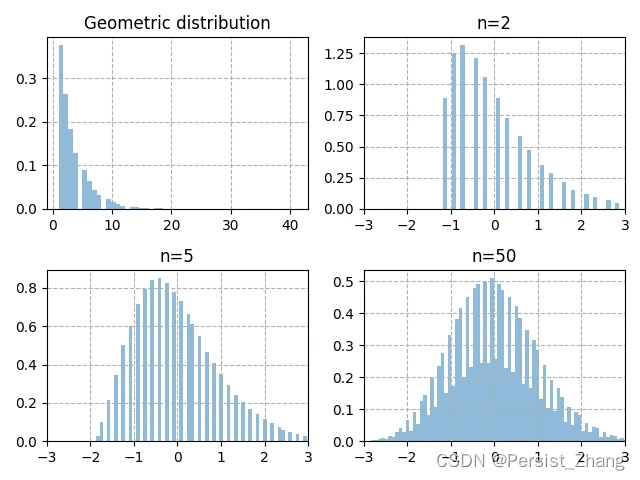
在这里插入图片描述
由图可知，左上是几何分布的原始图像，随着单次采样个数的增加，随机变量的分布图像越来越趋近于一个标准正态分布。

用大样本数据计算出的频率去估计概率，也就是大数定律，典型应用是蒙特卡洛方法。
此处利用蒙特卡洛方法来近似计算一个圆的面积，然后估计出 $\pi$ 的近似值。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
from matplotlib.patches import Circle


n = 100000
r = 1.0
o_x, o_y = (0., 0.)

uniform_x = uniform(o_x - r, 2 * r).rvs(n)
uniform_y = uniform(o_y - r, 2 * r).rvs(n)

d_array = np.sqrt((uniform_x - o_x) ** 2 + (uniform_y - o_y) ** 2)

res = sum(np.where(d_array < r, 1, 0))

pi = (res / n) / (r ** 2) * (2 * r) ** 2

fig, ax = plt.subplots()
ax.plot(uniform_x, uniform_y, 'ro', alpha=0.2, markersize=0.3)
plt.axis('equal')
circle = Circle(xy=(o_x, o_y), radius=r, alpha=0.3, ls='--')
ax.add_patch(circle)

print(f'pi = {pi}')
plt.grid(ls ='--')
plt.show()

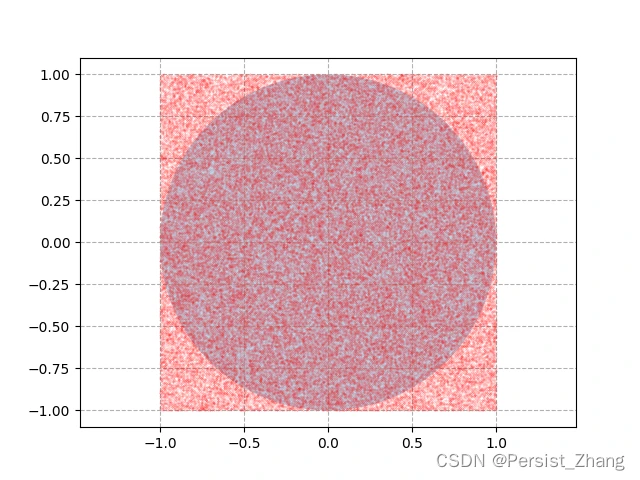
在这里插入图片描述
近似计算的目标是求图中半径 $r = 1$ 的单元圆面积，而这个单元圆的外接正方形的边长 $l = 2 r = 2$ ，因此，外接正方形的面积为4。代码中生成100,000个在外接正方形内均匀分布的点。均匀地撒下去，简述就是：
$\frac{圆形面积}{正方形面积} ≈ \frac{圆内点的个数}{点的总个数}$
这样就可以估算出单元圆的面积。为了估算 $\pi$ ，可以得到如下公式：
$\frac{\pi r^2}{(2r)^2}≈ \frac{圆内点的个数}{点的总个数}=>\pi≈ 4 *\frac{圆内点的个数}{点的总个数}$
随着样本数量增大， $\pi$ 值会越来越趋近于真实值，样本无穷大的时候收敛于真值。

概率基础——中心极限定理

引言

中心极限定理的表述

推导过程

中心极限定理模拟

知秋君

相关推荐