本节的主要目的是用几张水平覆盖度大于30%的电子图片合成全景图.
-
图像获取
条件1 : 用数码相机拍摄水平覆盖度大于30%的几张图片.
举例: 从左往右拍摄三张图, 第一张和第二张之间的水平覆盖度大于30%, 第二张和第三张之间的水平覆盖度大于30%.
条件2 : 图像之间没有视差(disparity)存在.
举例:相机绕着投影中心转动
要么拍摄一个平面的对象,水平移动. -
对应点分析
把三幅图导入到电脑中,然后选取两副相邻图像之中至少四组对应点. -
单应性(Homography)计算
用奇异值分解(SVD singular value decomposition)去计算这个2D homography.得到两个必要的单应性矩阵.
首先就是要选取四组对应点.要求是任意三点不能共线.并且最好是一些特征点, 不然之后自己可能都找不到对应点在哪里.
把这些点都看做向量,从euclidian坐标系转到homograph.
具体转化如下: 如果再euclidian坐标系下, 坐标为(x,y), 那么转到homograph就是(x,y,1)
转化后,第一步要做的就是conditioning, 也就是归一化
为什么一定要做这一步?
1 对于任何尺度的缩放,原点不变,始终是(0,0,0) 清除了坐标变换的影响.
2 可以提高计算精度.
如何做?
1 平移: 先找出图像的中心点, 然后把这个中心点平移到原点, 其他点也做同样的平移变换,得到平移因子tx,ty.
2 缩放: 将这些点到原点的平均距离缩放为1, x方向和y方向分别计算(其他资料有的写的
2
\sqrt{2}
2,他们假设坐标方向是各同向性的, Sx, Sy相等)
这里我也不太懂, 区别在哪?
非各向同性归一化和各向同性归一化的区别:
https://mil.ufl.edu/nechyba/www/eel6562/course_materials/t9.3d_vision/hartley1997.pdf(我自己还没看)
第二步就是计算design matrix
什么是设计矩阵呢?
设计矩阵其实就代表的已知观测量(Known observations).
每行表示一个观测对象,每列表示观测向量的一个变量.
我们的最终目的是想得到H, 也就是homography matrix. 这个代表的是未知参数(Unknown parameters).
现在我们已经得到了四对归一化后的点,那么如何通过这四对点来得到他们之间的变换矩阵(homography)呢?
x’ = (u’ v’ w’), x = (u v w), 想要把x转化为x’,就需要一个homography矩阵 H = [a b c; d e f; g h j]. 这里采用Matlab写法, ";"为列分隔符, 每对点的转化都满足如下的关系式(关系式1).
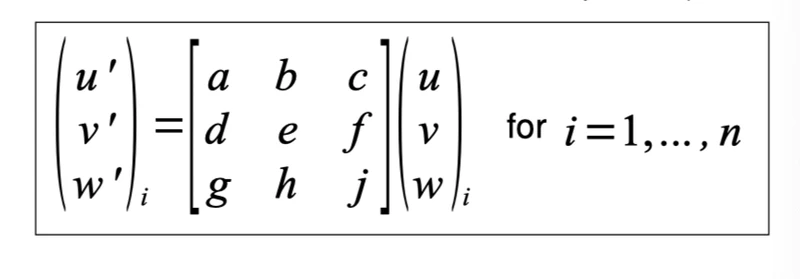
可以看到, 一共9个参数需要确定,但这九个参数实际上是由另外8个参数确定的.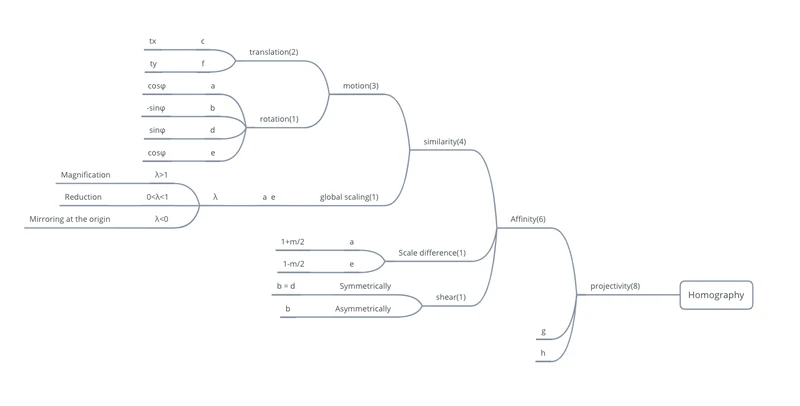
那么8个未知参数,至少需要八个线性无关的等式才可以解出.
通过关系式1,可以得出两个等式,也就是说,每对点可以解出2个未知参数.那么四对点就足够解出所以未知数.证明如下:
那么现在构造出一个设计矩阵,有n对点就可以构造出n(n>=4)个,再将这些设计矩阵合并为一个,命名为A,A是一个2n行9列的矩阵
通过前面的证明,可以知道Ah = 0
而h是H矩阵的变形.
Ah=0, 要求h其实是求A的零空间.
而零空间是Ah=0的解空间,Ah可以看成是矩阵A的所有的行向量分别和h做内积, 每一个行乘h(列向量)所得到的结果都是数字0(可见前面证明),所以每一个行向量都和h是正交的,所以h所在的空间与行空间是正交的,也就是零空间与行空间正交。当零空间不为空时,也就是Ah=0中的h可以取到不为0的解时,表明A的各个列向量之间线性相关.
通过SVD我们可以解出h.
SVD的证明明天写.
解出h以后,恢复为3*3的
H
~
\tilde{H}
H~,因为前面的x, x’都是经过归一化的点,所以得到homography也是归一化后的, 现在要解除归一化.
H=
T
′
⊺
\mathbf{T'}^\intercal
T′⊺
H
~
\tilde{H}
H~T.
证明: 传不上来!
假设三幅图,分别算出第一幅到第二副的矩阵和第三幅到第二幅的矩阵.
最后得到全景图.
参考:
https://www.cnblogs.com/lengyue365/p/7471608.html
上课用的PPT.(仅限内部使用)
