一、适用范围:
测试方法适用于所有芯片型号,用于测试ADC模块的INL/DNL参数,本文包含APT32F103X和APT32F171X的测试结果。
INL(积分非线性):ADC的INL指在失调 、增益误差被校正后,实际的传输曲线偏离理想中心线的程度,即:
DNL(微分非线性):在 ADC 实际传输曲线中,每个输出代码对应的输入电压宽度称为码宽,DNL指实际码宽电压与理想码宽电压 (LSB: Least Significant Bit) 之差,即:
INL和DNL计算是排除了OFFSET和GAINERROR干扰的,其计算值只与实际曲线曲线)和理论曲线有关,和理想曲线无关,因此offset的偏移和校准不会对INL和DNL值产生干扰。
二、测试原理:
本文采用的测试方法为直方图法(也称码密度法),其原理如下:
如果输入信号的概率密度分布为均匀分布(如斜波或者三角波),即输入电压在每个电压幅度上都是等概率的,那么,理想 ADC 的每个输出数字码也应该等概率。
实际中ADC由于存在非线性,每个数字码的 V 实际码宽和理想值有差异,从统计上讲,每个码箱的码密度直接与V实际码宽相应成正比,出现次数越多表明该代码的V实际码宽越大,非线性微分误差为正值;出现次数越少表明该代码V实际码宽越小,非线性微分误差为负值。
码密度反映了V实际码宽的大小,可以通过码密度来计算非线性微分误差,DNL可以由以下公式计算得出:
$$DNL=(P_{A(n)}/P_{I(n)})-1$$
其中,PA(n)代表实际ADC第n个数字码出现的概率,PI(n)代表理想 ADC 第 n 个数字码出现的概率。
INL理论上是对DNL进行积分运算,即对DNL进行累加求和得到。
注:直方图法中INL/DNL计算方法为概率学的等效计算方法,并不代表INL和DNL的实际含义,公式只在直方图法中有意义,INL/DNL的实际概念以适用范围中提到的为准。
三、测试环境:
测试芯片:APT32F103x, APT32F171x
芯片驱动:APT32F103x_latest APT32F171x_latest
测试工具:是德E36106B,信号发生器RIFOL DG1032
四、测试方法:
1.代码配置ADC单通道连续采样,ADC配置连续重复采样次数512次,平均系数512(以103为例)。
void adc_dnl_test_lin(void) //adc dnl
{
csi_adc_config_t tAdcConfigLin;
const csi_adc_seq_t tSeqCfgLin[] =
{ //输入通道 //连续重复采样次数 //平均系数 //触发源选择
{ADCIN0, ADC_CV_COUNT_512, ADC_AVG_COF_512, ADCSYNC_NONE},
};
uint16_t hwData[sizeof(tSeqCfgLin)/sizeof(tSeqCfgLin[0])];
uint8_t bySeqNum = sizeof(tSeqCfgLin)/sizeof(tSeqCfgLin[0]);// int hData;
csi_pin_set_mux(PB01, PB01_ADC_AIN0); //ADC GPIO作为输入通道
//adc 参数配置初始化
tAdcConfigLin.byClkDiv = 0x02; //ADC clk两分频:clk = pclk/2
tAdcConfigLin.bySampHold = 0x06; //ADC 采样时间: time = 16 + 6 = 22(ADC clk周期)
tAdcConfigLin.byConvMode = ADC_CONV_CONTINU; //ADC 转换模式: 连续转换;
tAdcConfigLin.byVrefSrc = ADCVERF_VDD_VSS; //ADC 参考电压: 系统VREFP/N
tAdcConfigLin.wInt = ADC_INTSRC_NONE; //ADC 中断配置: 无中断
tAdcConfigLin.ptSeqCfg = (csi_adc_seq_t *)tSeqCfgLin; //ADC 采样序列: 具体参考结构体变量 tSeqCfg
csi_adc_init(ADC0, &tAdcConfigLin); //初始化ADC参数配置
csi_adc_set_seqx(ADC0, tAdcConfigLin.ptSeqCfg, bySeqNum); //配置ADC采样序列
csi_adc_start(ADC0);
while(1)
{
hwData[0] = csi_adc_read_channel(ADC0, 0);
my_printf("%d ",hwData[0]); //
}
}2.由于斜波的概率密度为均匀分布,计算较为简单,因此采用斜波信号(三角波)进行测试,使用信号发生器向配置的ADC管脚输入频率为10mHz,电压为0-VCC(由于测试板的的实际VCC电压往往不是标准的5V,而VCC电压是ADC的参考电压,所以实际电压设置为0-实际VCC电压值)的三角波。

3.使用串口打印ADC采集到的数据,保存为TXT格式,采集的数据最少为2471680个。
注:由于直方图法本质上是一种统计方法,因此ADC采样点越多,结果越准确,对于一个12位的ADC,要求其置信度水平为95%,DNL 的误差为0.1LSB,则采样点数为2471680个。
4.使用MATLAB进行对采集到的数据进行处理(直方图法)。
clc % 清除所有命令
clear % 清除工作空间的所有变量,函数,和MEX文件
close all % 关闭所有的Figure窗口
start_pos=90870; %截取的开始位置
end_pos=1931000; %截取的结束位置
index1=1; %计数变量1
index2=1; %计数变量2
vref=5.0; %参考电压
use_tempdata=zeros(1,3000000); %处理后的数据,按use_data(x)访问
%打开adc_raw.txt文件,得到文件句柄id
fid=fopen('85_103_2.txt','r');
%把对应文件id的数据读到f中
%这里'%d'表示读取数据的格式
%这里'Inf'表示读取完整个文件
[raw_data,count]=fscanf(fid,'%d',Inf);
%关闭文件
fclose(fid);
%原始数据的作图
raw_data=raw_data'-999;
%大于4095的数全部剔除
while true
[raw_max,raw_index]=max(raw_data);
if raw_max>4096
raw_data(raw_index)=[];
else
count=length(raw_data);
break;
end
end
t=(0:1:count-1); % 0-count-1之间,间距1 count个数据
subplot(411);%四行1列第1个图
plot(t,raw_data);%samp singal
xlabel('t');%x轴标注
ylabel('y(t) code');%y轴标注
title('Ramp (raw_data)');%图标题
%原始数据的截取
start_pos=input("请输入截取数据起始位置:");
end_pos=input("请输入截取数据结束位置:");
for index1=start_pos:end_pos
if index2 > 3000000
break;
end
use_tempdata(index2)=raw_data(index1);
index2 = index2 +1;
end
%截取后数据的作图
t1=(0:1:end_pos-start_pos-1); % 0-count-1之间,间距1 count个数据
use_data=use_tempdata(1:end_pos-start_pos);
subplot(412);%四行1列第2个图
plot(t1,use_data);%samp singal
xlabel('t1');%x轴标注
ylabel('y(t1) code');%y轴标注
title('Ramp (use_data)');%图标题
grid on;
%dnl实际码值概率直方图和理论码值概率直方图
hist_data=hist(use_data,4096);%实际码值理论计算
hist_data1=hist_data/(end_pos-start_pos);
hist_idle = zeros(1,4096); %理论码值概率计算
hist_idle(1:4096) = 1/4096; %赋值理论概率
subplot(413);%四行1列第3个图
plot((1:1:4096),hist_data1);
hold on;
plot((1:1:4096),hist_idle,'r','LineWidth',2);
hold off;
xlabel('code bin');%x轴标注
ylabel('Pa and Pi');%y轴标注
title('DNL The code value probability');%图标题
%ramp dnl计算
dnl_data=hist_data1/(1/4096);
dnl_data=dnl_data-1;
dnl=max(abs(dnl_data));
%inl实际码值概率直方图和理论码值概率直方图
inl_data=cumsum(dnl_data);
inl=max(abs(inl_data));
figure;
plot((1:1:4096),dnl_data);
hold on;
plot((1:1:4096),inl_data,'r');
hold off;
xlabel('code');%x轴标注
ylabel('vol/v'); %y轴标注
title('INL error');%图标题
fprintf('dnl is: %d (LSB)\n',dnl);
fprintf('inl is: %d (LSB)\n',inl);5.读取matlab运行后的INL/DNL数据。
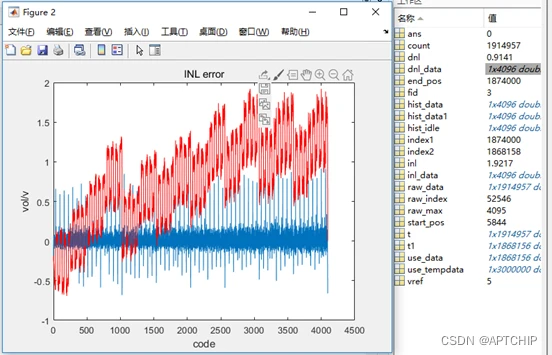
五、测试结果:
红色为INL_DATA的曲线,蓝色为DNL_DATA的曲线,由于INL和DNL标示的是ADC的精度。它是指ADC器件在所有的数值点上对应的模拟值和真实值之间误差最大的那一点的误差值,表示测量值的绝对误差,所以最终的INL和DNL为INL_DATA和DNL_DATA中绝对值最大的那一个。
APT32F103x
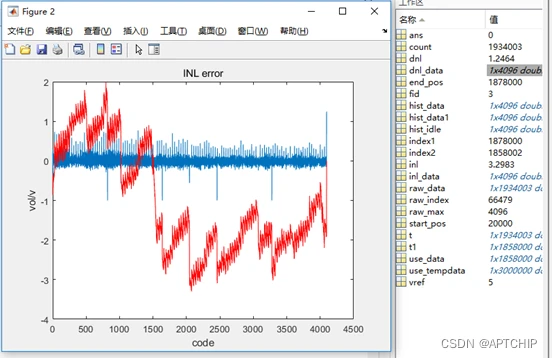
APT32F171x