👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
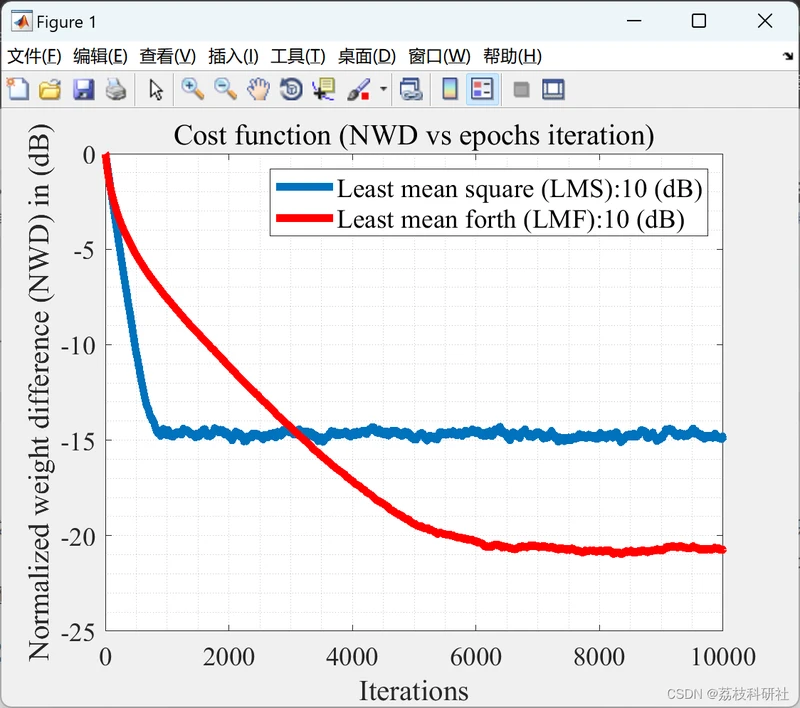
在本文中,在非高斯噪声环境中比较最小均方(LMS)和最小均方(LMF)算法,以执行系统识别任务。众所周知,LMF算法在非高斯环境中优于LMS算法,在此实现中可以看到相同的结果。此外,还编程了用于添加白色均匀噪声的定制功能。
📚2 运行结果
部分代码:
N = 1e4; % Number of samples
Bits = 2; % For PSK modulation
SNR = 10; % Noise level
% *Monte Carlo simulations*
% h = [0.9 0.2 0.5 -0.7]; % Plant1 impulse response
% h = [-2:1:2]; % Plant2 impulse response
h = randn(1,5); % Random system
runs=100;
NWDs = 0;
NWDf = 0;
temp3 = 0;
temp4 = 0;
for run = 1:runs % Monte Carlo simulations
% h = randn(1,5);
data = randi([0 (2^Bits)-1],1,N); % Random index for input data
x = real(pskmod(data,2^Bits)); % Phase shit keying (PSK) modulation
r = filter(h,1,x); % Input passed trought system(h)
d = awun(r, SNR); % Addition of white Uniform noise of decined SNR
% d = awgn(r, SNR); % Addition of white Gaussian noise of decined SNR
% *LMS parameter*
etas = 1e-2; % Learning rate for LMS
Wlms = zeros(size(h)); % Initial weights of LMS
Us = zeros(1,length(h)); % Input frame length of LMS
% *LMF parameter*
etaf = 1e-2; % Learning rate for LMF
Wlmf = zeros(size(h)); % Initial weights of LMF
Uf = zeros(1,length(h)); % Input frame length of LMF
for n = 1 : N
% *LMS*
Us(1,2:end) = Us(1,1:end-1); % Shifting of frame window
Us(1,1) = x(n); % Input of LMS
ys = (Wlms)*Us'; % Output of LMS
es = d(n) - ys; % Instantaneous error of LMS
Wlms = Wlms + etas * es * Us; % Weight update rule of LMS
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
@article{Khan2017FLMFFL,
title={FLMF: Fractional least mean fourth algorithm for channel estimation in non-Gaussian environment},
author={Shujaat Khan and Naveed Ahmed and Muhammad Ammar Malik and Imran Naseem and Roberto Togneri and Mohammed Bennamoun},
journal={2017 International Conference on Information and Communication Technology Convergence (ICTC)},
year={2017},
pages={466-470}

