数学建模笔记-斜抛运动建模
作者:Peiy_Liu
日期:2020-02-04
1. 数学模型
质量为m的质点作斜抛运动,假定质点出射后,只受到恒力
m
g
m\bf{g}
mg和空气阻力
f
\bf{f}
f作用,其中f的大小与速度大小的平方成正比,方向与速度相反,即
f
=
−
k
v
2
(1.1)
f=-kv^2 \tag{1.1}
f=−kv2(1.1)则质点始终在初速度确定的竖直平面内运动,在质点运动平面内以高度为0处一点为原点,水平方向为
x
x
x轴,竖直方向为
y
y
y轴建立坐标系。令
r
\bf{r}
r
=
[
x
y
]
T
= \left[\begin{matrix}x&y\end{matrix}\right]^T
=[xy]T为质点的位矢,由牛顿第二定律列出质点动力学方程
f
+
m
g
=
m
r
¨
(1.2)
{\bf{f}}+m{\bf{g}}=m\ddot{\bf r} \tag{1.2}
f+mg=mr¨(1.2)由于空气阻力方向与速度方向相反,
f
\bf{f}
f可写为
f
=
−
k
v
2
e
=
−
k
[
x
˙
x
˙
2
+
y
˙
2
y
˙
x
˙
2
+
y
˙
2
]
(1.3)
{\bf{f}}=-kv^2{\bf{e}}=-k\left[\begin{matrix}\dot{x}\sqrt{\dot{x}^2+\dot{y}^2}\\\dot{y}\sqrt{\dot{x}^2+\dot{y}^2}\end{matrix}\right] \tag{1.3}
f=−kv2e=−k[x˙x˙2+y˙2y˙x˙2+y˙2](1.3)式中
e
=
[
1
/
1
+
y
′
2
y
′
/
1
+
y
′
2
]
T
{\bf{e}}=\left[\begin{matrix}1/\sqrt{1+y'^2}&y'/\sqrt{1+y'^2}\end{matrix}\right]^T
e=[1/1+y′2y′/1+y′2]T为质点速度方向的单位矢量.由此,式(1.2)可写成一个二阶微分方程组
{
m
x
¨
=
−
k
x
˙
x
˙
2
+
y
˙
2
m
y
¨
=
−
k
y
˙
x
˙
2
+
y
˙
2
−
m
g
(1.4)
\begin{cases}m\ddot{x}=-k\dot{x}\sqrt{\dot{x}^2+\dot{y}^2}\\m\ddot{y}=-k\dot{y}\sqrt{\dot{x}^2+\dot{y}^2}-mg\end{cases}\tag{1.4}
{mx¨=−kx˙x˙2+y˙2my¨=−ky˙x˙2+y˙2−mg(1.4)再令
z
1
=
x
˙
,
z
2
=
y
˙
z_1=\dot{x},z_2=\dot{y}
z1=x˙,z2=y˙方程组(1.4)化为形如
Y
′
=
f
(
t
,
Y
)
(1.5)
{\bf Y'}={\bf f}(t,{\bf Y})\tag{1.5}
Y′=f(t,Y)(1.5)的标准形式
{
z
1
˙
=
−
k
z
1
z
1
2
+
z
2
2
/
m
z
2
˙
=
−
k
z
2
z
1
2
+
z
2
2
/
m
−
g
(1.6)
\begin{cases}\dot{z_1}=-kz_1\sqrt{z_1^2+z_2^2}/m\\\dot{z_2}=-kz_2\sqrt{z_1^2+z_2^2}/m-g\end{cases}\tag{1.6}
{z1˙=−kz1z12+z22/mz2˙=−kz2z12+z22/m−g(1.6)
就可以用MATLAB中提供的函数求解了。
2. MATLAB建模
2.1 MATLAB解常微分方程
很多常微分方程难以求出解析解,需要运用数值解法,如方程组(1.6)。MATLAB提供了如ode45、ode23、ode113等函数可以解出形如式(1.5)的常微分方程(组)的数值解,通用用法为
[T,Y] = solver(fun,tspan,y0)
solver可用ode45、ode23、ode113中的任意一个替代,fun为等式右边的 f \bf f f向量,它所代表的M文件须有如下形式
function dy = fun(t,y)
dy = ...
不管是否在fun中用到,fun一定有两个参数t和y。tspan为求解区间向量,y0为初值向量。返回值中T是自变量的取值,Y的各列为数值解。对由一个高阶常微分方程化为的方程组。Y(:1)是对应t的初值解,Y(:n)为对应t处初值解的n-1阶导数。
2.2 编程求轨迹
先用上述方法解出 z 1 , z 2 z_1,z_2 z1,z2(即 v x , v y v_x,v_y vx,vy),再对分速度分别进行数值积分则可得到轨迹上的点 ( x , y ) (x,y) (x,y),最后可使用plot()函数绘出轨迹图。下面是代码
m = 2; %质点质量kg
k = 0.50; %空气阻力f = -k * v^2,国际单位
g = 9.8; %重力加速度
theta = pi / 4; %出射仰角rad
v0 = 20; %初速度大小
vx0 = v0 * cos(theta);
vy0 = v0 * sin(theta);
z0 = [vx0, vy0]; %构造微分方程组
x0 = 0;
y0 = 0;
f = @(t,z) [-k * z(1) * sqrt(z(1)^2 + z(2)^2) / m; -k * z(2) * sqrt(z(1)^2 + z(2)^2) / m - g];
[T, Z] = ode45(f, [0, 1.5], z0);
vx = Z(:,1);
vy = Z(:,2);
x = x0;
y = y0;
for i = 1:length(T)-1 %手动数值积分
tempx = x(i) + vx(i) * (T(i+1) - T(i));
tempy = y(i) + vy(i) * (T(i+1) - T(i));
x = [x;tempx];
y = [y;tempy];
end
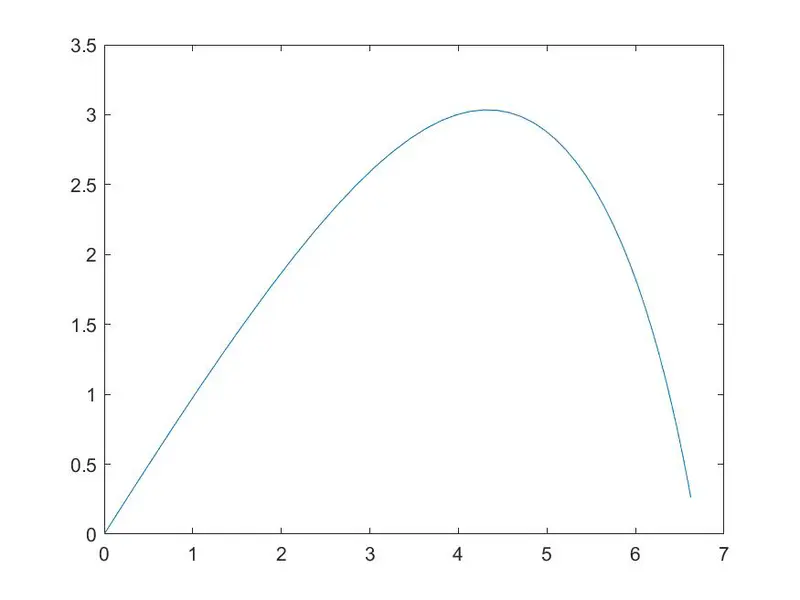
plot(x, y)
运行效果如图
##参考文献
司守奎《数学建模算法与应用》
