多面体编译基础（一）-- 从代码语法到多面体表示

写在前面

声明

本系列文章翻译自俄亥俄州立大学计算机科学与工程系Louis-Noël Pouchet教授Polyhedral Compilation Foundations课程的课件，对课件内容酌情筛选，并增加一些个人的内容，如存在错误或待争议部分，望各位同行（大佬）指正。

文章格式标准：

文章中出现的程序代码默认为C/C++格式

符号表

为什么要学习多面体编译

课程简介

学习目标

学会多面体编译技术中涉及到的基本数学概念。
建立对某些重要数学结论的记忆。
了解多面体便以技术的原理。

多面体程序优化三步走战略

分析：从代码到模型
模型变换
代码生成：从模型到代码

上述过程可概括为：从实例到规律，再从规律到实例。

本章内容

凸集（Convexity Set）
多面体（Polyhedra）
晶格（Lattices）

一、迭代域的几何表示

1.1 启发例子

先看一看如下所示的嵌套循环：

for (i = 0; i < 3; ++i)
    for (j = 0; j < 3; ++j)
        A[i][j] = i * j;

上述代码段的指令执行过程为：

A[0][0] = 0 * 0;
A[0][1] = 0 * 1;
A[0][2] = 0 * 2;
A[1][0] = 1 * 0;
A[1][1] = 1 * 1;
A[1][2] = 1 * 2;
A[2][0] = 2 * 0;
A[2][1] = 2 * 1;
A[2][2] = 2 * 2;

通过观察上述指令执行过程我们可以得到一些规律：

数组A的赋值语句被执行了9次
每次给A赋值时数组索引i、j都不同
语句的执行是存在顺序的

那么我们目标即为找到能够适当描述上述三个规律的模型。

1.2 迭代域（Iteration Domain）

迭代域是一种由迭代向量构成的集合（或线性空间），在上面的例子中，对于数组元素A[i][j]，迭代向量可表示如下：

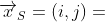
$\overrightarrow{x}_{S}=(i,j)$

其中，S的含义为（Statement），表示用于迭代的语句；i，j皆表示迭代索引。在定义迭代向量后，我们可以通过构造线性不等式组来描述上面例子对应的迭代空间：

我们观察到上面的例子中i、j在迭代中的取值范围分别为：

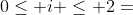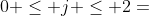
$0\leq i \leq 2$ ， $0 \leq j \leq 2$

改写为向量形式，得：

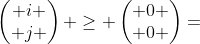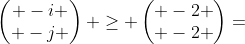
$\begin{pmatrix} i \\ j \end{pmatrix} \geq \begin{pmatrix} 0 \\ 0 \end{pmatrix}$ ， $\begin{pmatrix} -i \\ -j \end{pmatrix} \geq \begin{pmatrix} -2 \\ -2 \end{pmatrix}$

合并上述两项，得到完整的不等式组：

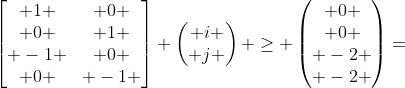
$\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ -1 & 0 \\ 0 & -1 \end{bmatrix} \begin{pmatrix} i \\ j \end{pmatrix} \geq \begin{pmatrix} 0 \\ 0 \\ -2 \\ -2 \end{pmatrix}$

该不等式组即表示了上面例子中的迭代域，该迭代域是一个二维多面体，也是一个凸集，画在二维平面坐标系上如下图所示：