考试地址:2022XD招生选拔_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ
密码:chouxiaogong
个人整体感受:难度中等,没有特别难的题,对思维,时间复杂度优化有一定的考察。
A.坐标纸中数个数
题目描述
Ruri最近学上了组合数学。有一天,他拿着坐标纸开始愉快的玩耍。他们知道,在同一条直线的三个点是不能构成三角形的。然后,他们盯着坐标纸开始发呆阿,发呆阿,发呆。给定一个 m 和一个 n ,这样就给定了在坐标纸上的一个 m×n大小的矩形,有 (m+1)×(n+1)个格点。他想让聪明的你来计算,三点都在格点上的三角形共有多少个。
输入描述:
共 T(1≤T≤90)组数据。输入一行,蓝蓝给定的 m(1≤m≤1000)和红红给定的 n(1≤n≤1000) ,中间间隔一个空格符。
输出描述:
对每组数据,每行输出一个正整数,为所求三角形数量。
示例1
输入:
2
1 1
2 2
输出:
4
76
---------------------------------------------------------------------------------------------------------------------------------
一共有total=(m+1)*(n+1)个点,任意选三个的总数很容易算出来是C(total,3),现在需要除去共线的方案。
水平的情况很好算,主要是斜着的情况。这里涉及到一个公式,在网格上如果给定两个整点的坐标(x1,y1);(x2,y2),可以通过公式gcd(x2-x1,y2-y1)-1算出两点连线所经过的整点个数(考虑斜率相等建立方程易证)。
只要枚举两个点的位置,就可以计算出所有共线的方案,复杂度是O(n^4),本题数据量是1000,需要控制到O(n^2).
考虑把一个点固定在原点,只枚举一个点(i,j),可以发现对于每一种线段,它在整个网格中出现了(n-i+1)*(m-j+1)次。
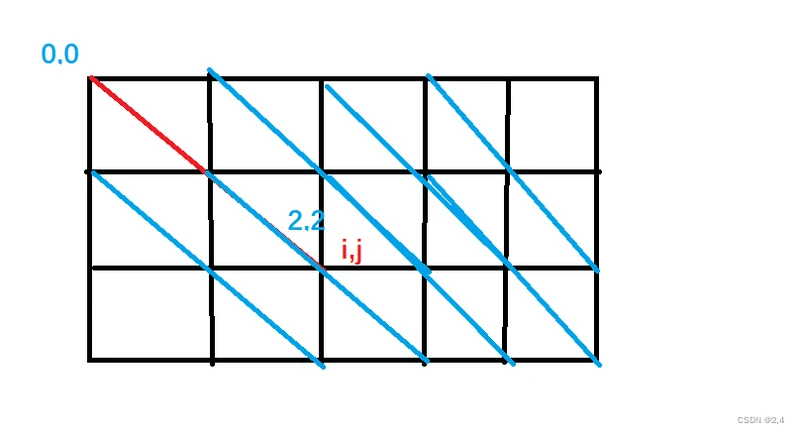
画个图感受一下:枚举到(2,2),图中红色的线中间有1个点,移动原点,向右就有4种摆放,向下有2种摆放。所以就有8个不合法方案。
还要注意,这里我们只球出了斜率为正的情况,斜率为负其实是等效的,对于每一种线段两者是对称的。(斜率为0单独处理)
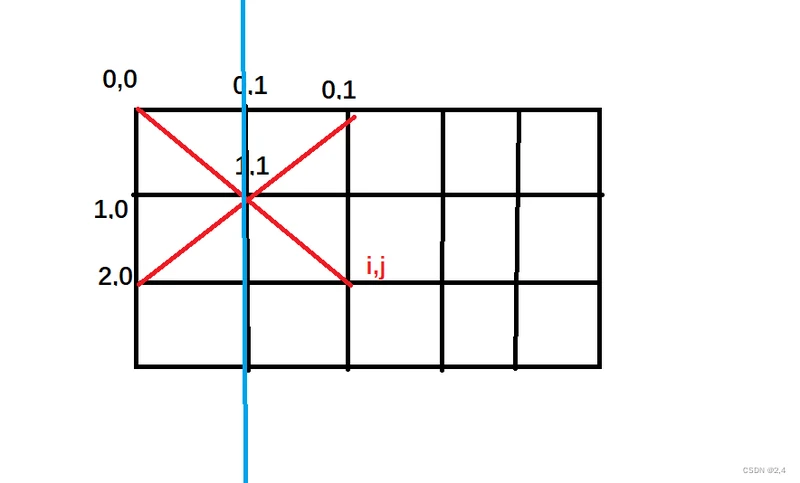
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=510;
typedef long long ll;
ll C(int k)
{
if(k<3) return 0;
return 1ll*k*(k-1)/2*(k-2)/3;
}
int main()
{
int T;
cin>>T;
while(T--){
int m,n;
cin>>n>>m;
ll ans=C((m+1)*(n+1));
for(int i=0;i<=n;++i)
for(int j=0;j<=m;++j){
if(i==0&&j==0) continue;
if(i==0||j==0) ans-=(__gcd(i,j)-1)*(n-i+1)*(m-j+1);
else ans-=2*(__gcd(i,j)-1)*(n-i+1)*(m-j+1);
}
cout<<ans<<endl;
}
return 0;
}B.特殊符号组CP
题目描述
Ruri最近迷上了组 cp 。他们在想,所有的特殊符号,是不是也可以组成 cp 。如何组成 cp 呢?
(1)空串 s ,组成了 cp 。
(2)一个包含有数字、大小写字符的字符串s,组成了 cp 。
(3)特殊符号仅包含大 {} 中 [] 小 () 括号。
(4)若 s 组成了 cp,则 (s)、[s]、{s} 组成了 cp。
(5)若 s 组成了 cp ,t 组成了 cp,则 st 与 ts 组成了 cp 。
Ruri想偷懒,请问你,对于某一个字符串,是否组成 cp 了呢?
输入描述:
共 T(1≤T≤100)组数据。 每组数据为一个给定一个长度为 100 的字符串。
输出描述:
每组数据输出一行。 如果组成cp,则输出 cp good,不带引号,末尾带一个换行符。 如果组不成cp,则输出 cp bad,不带引号,末尾带一个换行符。
示例1
输入:
5
1A2B3C
{123}
{123}[123]
{[123]}
!*(123)*!!
输出:
cp good
cp good
cp good
cp good
cp bad
---------------------------------------------------------------------------------------------------------------------------------
符号匹配的模板题,用栈模拟,对不上就false,不多解释。
code:
#include<bits/stdc++.h>
using namespace std;
const int N=510;
string s;
bool judge()
{
stack<char>st;
for(int i=0;i<s.size();++i){
if(isdigit(s[i])) continue;
if(isalpha(s[i])) continue;
if(s[i]=='('||s[i]=='['||s[i]=='{') st.push(s[i]);
else if(s[i]==')'){
if(st.empty()||st.top()!='(') return false;
else st.pop();
}
else if(s[i]==']'){
if(st.empty()||st.top()!='[') return false;
else st.pop();
}
else if(s[i]=='}'){
if(st.empty()||st.top()!='{') return false;
else st.pop();
}
else return false;
}
if(st.empty()) return true;
return false;
}
int main()
{
int t;
cin>>t;
while(t--){
cin>>s;
if(judge()) puts("cp good");
else puts("cp bad");
}
return 0;
}C.Xor to K
题目描述
Ruri 非常喜欢数字 K ,现在有 n 个数 a1,a2,⋯ ,an,Ruri 想从中选出一些数使得他们的异或和为 K ,请问有多少种选择的方案?
两种方案视为不同当且仅当两个方案选的数的个数不同或者个数相同但至少存在一个数两者选的不同。当且仅当两个方案选的数的个数不同或者个数相同但至少存在一个数两者选的不同。
输入描述:
第一行为两个正整数。第二行有 n个数表示。第一行为两个正整数 n(1≤n≤40),k(1≤k≤1e9)。第二行有 n个数表示 a1,a2,⋯ ,an(1≤ai≤1e9)。
输出描述:
第一行为两个正整数 n(1≤n≤40),k(1≤k≤1e9)。第二行有 n个数表示 a1,a2,⋯ ,an(1≤ai≤1e9)。
示例1
输入:
4 2
4 2 6 4
输出:
4
---------------------------------------------------------------------------------------------------------------------------------
考虑暴力集合枚举每一个选择状态,复杂度2^n,本题n的大小为40.
优化:一切算法都来源于二分(bushi),把数组分成两份,这样先枚举第一份的选择状态,并存下每个状态的异或值a,在枚举第二份的选择状态,算出异或值b,合法方案为a^b=k,即b=a^k,a的个数已经算出来了,因此加上就可以了。复杂度为O(2*2^(n/2)).
code:
#include<bits/stdc++.h>
using namespace std;
const int N=45;
typedef long long ll;
int a[N];
vector<int>p,l;
unordered_map<ll,int>mp;
int main()
{
int n,k;
ll ans=0;
cin>>n>>k;
for(int i=0;i<n;++i){
cin>>a[i];
if(i<=n/2) p.push_back(a[i]);
else l.push_back(a[i]);
}
for(ll i=0;i<1<<p.size();++i){
ll res=0;
for(int j=0;j<p.size();++j) if(i&(1<<j)) res^=p[j];
mp[res]++;
}
for(ll i=0;i<1<<l.size();++i){
ll res=0;
for(int j=0;j<l.size();++j) if(i&(1<<j)) res^=l[j];
if(mp.count(res^k)) ans+=mp[res^k];
}
cout<<ans;
return 0;
}D.队列
题目描述
Ruri看到了一个行进中的队列,他突然想到一个问题。
这个队列只有一列人,要么是男生,要么是女生,男生用M代替,女生用F代替,可以看成一个只包含M或F的字符串。
他想知道这个字符串包含M,F数量相同的最长子串长度是多少。
输入描述:
输入一个只包含M或F的字符串,长度≤5e5
输出描述:
输出一个数字,表示最长子串长度。如果不存在就输出Impossible
示例1
输入:
MMFF
M
MMMMFFMF
输出:
4
Impossible
6
---------------------------------------------------------------------------------------------------------------------------------
类似于前缀和的思想。假设M表示1,F表示-1(反过来也可以),遍历s,用一个cnt记录当前的值,可以发现第i个cnt就是记录的从0~i的值,如果为0相当于抵消了,更新长度。否则需要把左端点向右移动,并且为了向右移动的越少越好,如果cnt=x,我们只需要从开头-x即可,那么只需要找到第一个出现x的下标,可以记录下来。
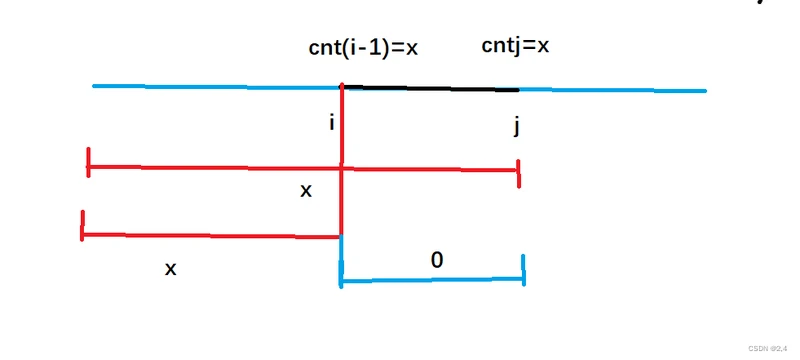
code:
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int main()
{
string s;
while(cin>>s){
unordered_map<int,int>mp;
int cnt=0,ans=0;
for(int i=0;i<s.size();++i){
if(s[i]=='M') ++cnt;
else --cnt;
if(cnt==0) ans=max(ans,i+1);
else if(mp.count(cnt)) ans=max(ans,i-mp[cnt]);
else mp[cnt]=i;
}
if(ans) cout<<ans<<endl;
else puts("Impossible");
}
return 0;
}E.A+B-C-D=X
题目描述
给定两个正整数N和X,Ruri 想知道有多少个不同的四元组(A,B,C,D)满足 A+B-C-D=X?
两个四元组相同的充分必要条件是对应位置的每个元素值相同。
输入描述:
第一行一个正整数 T(1≤T≤100),表示有T组测试数据。 接下来TTT行每行两个正数 N(1≤N≤103),X(1≤X≤103) 其中 1≤A,B,C,D≤N 保证 ∑TN≤1e4
输出描述:
T 行,每行一个整数表示答案。
示例1
输入:
4
2 2
4 5
3 5
7 6
输出:
1
4
0
84
---------------------------------------------------------------------------------------------------------------------------------
日本算法竞赛大佬的白书中有提到这个处理方法。
需要找到A+B-C-D=X,即A+B=X+C+D,那么我们先预用O(n^2)的复杂度处理出A+B(C+D)的所有可能情况。然后做排序,注意到重复的元素需要视为不同的方案。做去重操作,把重复元素的个数要记录下来。
注意到A+B>C+D,只需要枚举C+D,然后用二分法找到在数组中找到X+C+D的值即可。
code:
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int a[N],b[N];
int main()
{
int T;
cin>>T;
while(T--){
vector<int>v;
int n,x;
cin>>n>>x;
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j) v.push_back(i+j);
sort(v.begin(),v.end());
int cnt=0,al=0;
for(int i=0;i<v.size();++i){
int c=1;
while(i+1<v.size()&&v[i]==v[i+1]) ++c,++i;
a[al++]=c,b[al-1]=v[i];
}
for(int i=0;i<al;++i){
int p=lower_bound(b,b+al,b[i]+x)-b;
if(p==al) break;
if(b[i]+x==b[p]) cnt+=a[i]*a[p];
}
cout<<cnt<<endl;
}
return 0;
}F.回文数
题目描述
Ruri得到了一个不包含前导零的数字 N ,他想知道在这个数字前面加上几个0能否使得整个数字变成回文串
输入描述:
一个正整数 n(1≤n≤10^(10^6))
输出描述:
可以变成回文串就输出 Yes,否则输出No。
示例1
输入:
1210
输出:
Yes
说明:
1210前面加上0是01210,是回文串
---------------------------------------------------------------------------------------------------------------------------------
只需要除去头部0和尾部0,只需要判断中间能不能构成回文串即可。
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int main()
{
string s;
cin>>s;
int k,m;
for(k=s.size()-1;k>=0;--k) if(s[k]!='0') break;
for(m=0;m<s.size();++m) if(s[m]!='0') break;
if(k<0) puts("Yes");
else{
int f=1;
for(int i=m,j=k;i<=j;++i,--j){
if(s[i]!=s[j]){
f=0;
break;
}
}
if(f) puts("Yes");
else puts("No");
}
return 0;
}G.硬币
题目描述
Ruri打算买一个价值为 KKK的商品,他有10种硬币,价值分别为 1!,2!,⋯ ,10!其中 n!=1×2×⋯n。每种都有100个,他想知道最少需用多少硬币,每种用多少个
输入描述:
一行,一个整数 K(1≤K≤107)
输出描述:
第一行一个正整数,表示需要的硬币数量。 之后10个数,用空格分开,代表每个硬币使用的个数,从左到右面值分别为 1!,2!,⋯ ,10!。行末无空格。
示例1
输入:
9
输出:
3
1 1 1 0 0 0 0 0 0 0
---------------------------------------------------------------------------------------------------------------------------------
开始没有注意到题目硬币上限是100,但是貌似数据并没有卡这个。
贪心算法,每一次都尽量选择最大硬币。
对于硬币为阶乘的数据,假设用贪心法得到了一个最优解,如果少用了一些比较大的硬币,需要更多的较小的硬币填充。
关于找零钱问题能不能用贪心法解决的深入研究这里不再探讨,有兴趣可以看cf的一道题:Greedy Change - 洛谷
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int v[]={1,2,6,24,120,720,5040,40320,362880,3628800},c[10];
int main()
{
int k,ans=0;
cin>>k;
for(int i=9;i>=0;--i){
c[i]=min(k/v[i],100),ans+=c[i];
k-=c[i]*v[i];
}
cout<<ans<<endl;
for(int i=0;i<10;++i) cout<<c[i]<<" ";
return 0;
}
