目录
一、编程语言
二、计算机基础
1、计算机系统的组成
2、计算机的工作过程
3、存储器
三、数制(二进制、八进制、十进制、十六进制)
1、二进制、八进制、十六进制转化为十进制
2、十进制转化为二进制、八进制、十六进制
3、二进制、八进制、十六进制之间的转换
4、二进制的运算
四、算法
1、描述算法的工具
2、算法的特性
一、编程语言
机器语言
编程语言分为 汇编语言
高级语言
而机器语言和汇编语言合称为低级语言。
1、机器语言:使用二进制进行指令的编译,是计算机可以直接识别的指令,因此是计算机执行效率最高的语言。
2、汇编语言:使用单词风格的符号代替二进制的操作指令,但是需要进行翻译才可以使计算机执行指令。
3、高级语言:容易被程序员所掌握,但是是计算机执行效率最低的语言。
二、计算机基础
1、计算机系统的组成
运算器
硬 控制器
件 存储器
计 系 输入设备
算 统 输出设备
机
系 操作系统
统 软 系统软件 数据库管理系统
件 语言处理程序
系
统 应用软件
<1>计算机的五个硬件是由冯·诺依曼提出
<2>运算器与控制器合称为CPU(中央处理器)
<3>运算器里面只存在加法器,只可以进行加和移位的操作,加减乘除都是通过加和移位完成的
2、计算机的工作过程
数据输入输入设备由控制器控制传入存储器,再由控制器控制从存储器中取出数据交给运算器进行运算,运算器运算完毕后由控制器控制存入存储器,再由控制器控制输出设备从存储器中取出数据。
※控制器相当于路口指挥交通
3、存储器
存储器的结构如下图所示,存储器是由一个个小房间构成的,一个小房间中有八根电线,电线通电代表1,不通电代表0
一个小房间代表一个字节(Byte)
一根电线代表一个位(bit比特位)
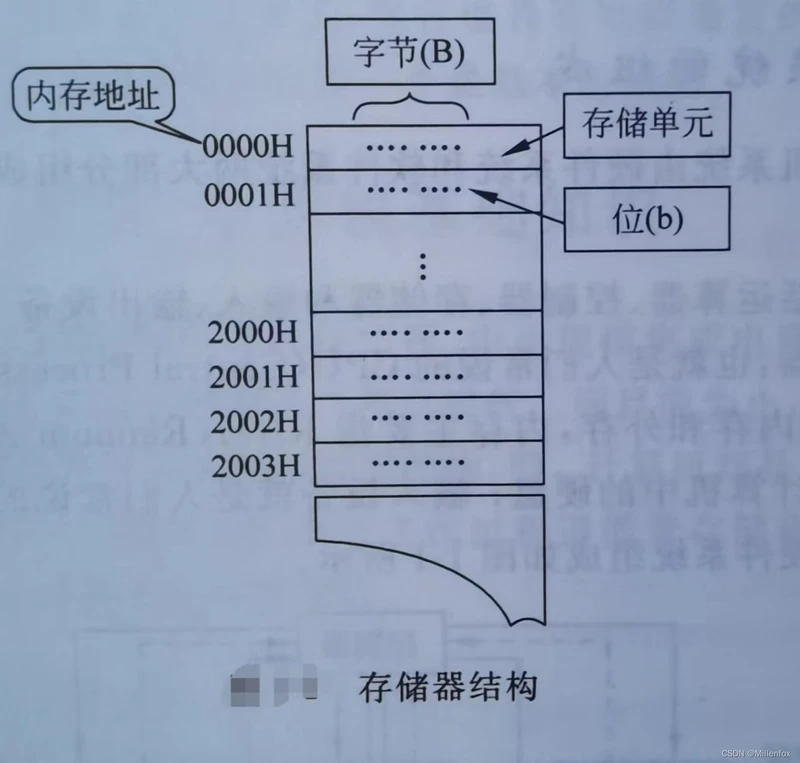
<1>如果一个房间存储数据不够,那么加房间时,房间的总数要是2的几次方个。比如:1个、2个、4个、8个、16个......
<2>整数分为 有符号整数:最高位为符号位,并不算数,最高位为1是负数,最高位为0是正 数。如:(1000 0101,这个数为-5)
无符号整数
<3>计算机中所存储的数据以补码的形式存放
正数:原码=反码=补码
负数:原码就是符号位为1,其余位为该数的绝对值。如:(1000 0011,-3原码)
反码即原码的符号位不变,其他位按位取反。如:(1111 1100,-3反码)
补码即反码+1,如(1111 1101,-3补码)
<4>存储器一个房间存储的数据
无符号整数:0(0000 0000)——255(1111 1111)
有符号整数:-128(1111 1111)——127(0111 1111)
存储器两个房间存储的数据
无符号整数:0(0000 0000 0000 0000)——65535(1111 1111 1111 1111)
有符号整数:-2的15次方(1111 1111 1111 1111)——2的15次方-1(0111 1111 1111 1111)
存储器四个房间存储的数据
无符号整数:0——2的32次方-1
有符号整数:-2的31次方——2的31次方-1
<5>单位换算
1B=8b(一字节等于八比特位)
1kb=1024B
1mb=1024kb
1gb=1024mb
1tb=1024gb
1pb=1024tb
三、数制(二进制、八进制、十进制、十六进制)
进制:进位计数制,是指用进位的方法进行计数的数制。
数码:是用来表述数的符号。如十进制的0、1、2、3、4、5、6、7、8、9
基数:数码的个数称为"基数"或"基",通常用R表示,称为R进制。
位权:数码在不同位置上的权值。如:十进制的164,1的权值为10²,6的 权值为10的一次方,4 的权值为10的零次方。
数制的表示方法:下标表示法:二进制()2 八进制()8 十进制()10 十六进制()16
后缀表示法:二进制B 八进制O 十进制D 十六进制H 如:0011H
1、二进制、八进制、十六进制转化为十进制

即不同位置上的数与其权值的乘积之和
2、十进制转化为二进制、八进制、十六进制

上图解释:十进制转化为二进制,整数部分就是将一个数不断除2,除到0,其余数从下往上组成整数部分的二进制数。小数部分就是将十进制的小数不断乘2直到结果为0(若结果一直不为0,那就截取适当位的小数),将小数乘2过程中产生的整数部分取出,从上往下读组成二进制数。
八进制和十六进制的与二进制的做法相同,只不过将除数和乘数换成对应的基数。
3、二进制、八进制、十六进制之间的转换
二进制中 1000表示8,10000表示16
因此二进制转换为八进制的方法为:整数部分从右边开始,每三个一组,转化为八进制,若最左边不足三位,则补零,小数部分从左边开始,每三个一组,转化为八进制,若最右边不足三位,则补零。如下:
对1011 1101.1001进行转换(绿色背景为补的零,三个一组)
01011 1101.100100
2 7 5 . 4 4
八进制转换为二进制,只需要反过来
2 7 5 . 4 4
010 111 101 . 100 100
二进制转换为十六进制的方法为:整数部分从右边开始,每四个一组,转化为十六进制,若最左边不足四位,则补零,小数部分从左边开始,每四个一组,转化为十六进制,若最右边不足四位,则补零。如下:
对1011 1101.1001进行转换(绿色背景为补的零,四个一组)
1011 1101.1001
B D . 9
十六进制转换为二进制,只需要反过来
B D . 9
1011 1101 . 1001
4、二进制的运算
<1>加法运算(+):对于有符号位的,符号位不参与运算,只有数据位参与运算。
<2>减法运算(-)
<3>与运算(&):只有两个相应的二进制位均为1,结果才为1。负数要用补码进行运算。
①清零,选择全零的二进制数,就可以将别的二进制数全部归零
②可以保留或者取特定位置上的数,保留或者取特定位置上的数只需用另一组 在此位置上均为1的二进制数与之进行与运算
<4>或运算(|):相应的二进制位至少有一个为1,结果就为1。
①可以将一些位置的数改为1
<5>非运算(~):将二进制数按位取反。非运算是单目运算符,优先级高于其他运算符。
<6>异或运算(^):相应的二进制位不相同就为1,相同就为0。
①异或运算符也叫做XOR运算符
②可以使指定位进行翻转
如果使某一位或多位的数进行翻转,就用一个相同位置上数为1,其余位置 上数为0的二进制数与之进行异或运算。如:对1010 0001的第二位和第三 位进行翻转,就用0000 0110与之进行异或。
③可以保留原来的值
一个数与零进行异或运算,得到原来的数,a^0=a
④可以交换两个变量的值:
a=a^b b=a^b a=a^b
★异或运算满足交换律和结合律: a^b=b^a
b^a^b=a^b^b
还满足 a^a=0
a^0=a
因此可以对④进行解释,a=a^b
b=a^b=a^b^b=a^(b^b)=a^0=a
a=a^b=a^b^a=b^(a^a)=b^0=b
四、算法
1、描述算法的工具
<1>自然语言描述(伪代码也属于这一类)
<2>图形:①流程图②N-S结构图
<3>程序
2、算法的特性
<1>有穷性:算法必须在有限的时间内结束
<2>确定性:不可存在二义性
<3>可行性:每一步都切实可行
<4>有零个或多个输入
<5>有一个或多个输出
