1. 成本函数

- 成本函数给我们提供了一种方法(他本身)来衡量一组特定的参数适不适合训练数据集
- 平方误差成本函数是最通常用于线性回归的成本函数
- 最终,我们要找到一组w和b,让J函数的值最小
- 误差:ŷ - y
2. 简化后的平方误差成本函数,即b = 0
- 当w = 1时,f(x) = x,J(1) = 0
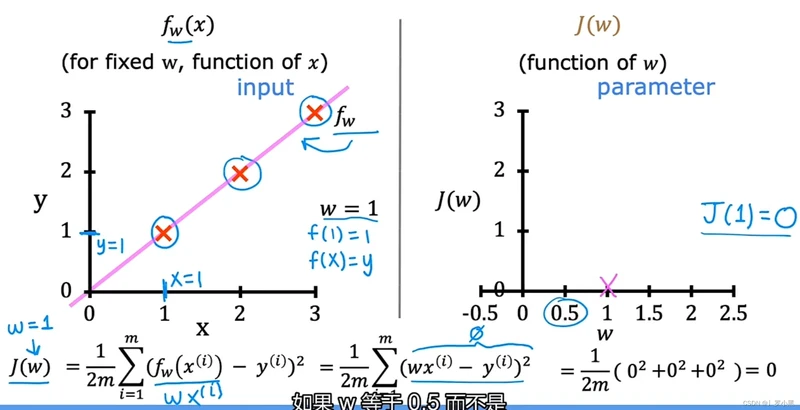
- 左侧为f(x)函数,X轴为x,❌表示训练示例
- 右侧为J(w)函数,X轴为w
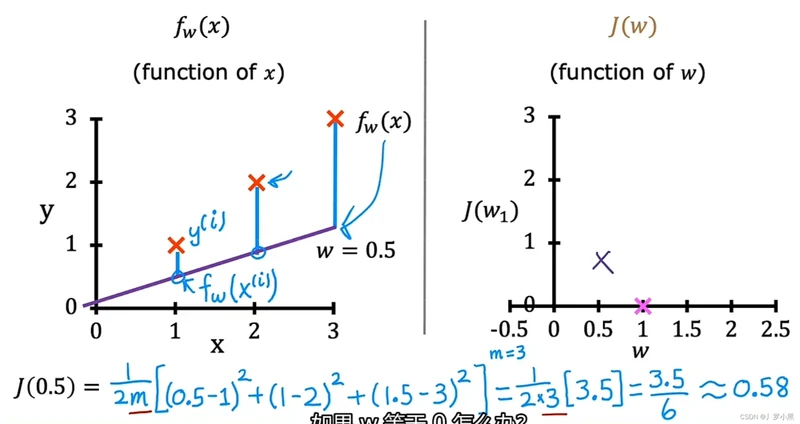
- 当w = 0.5时,f(x) = 0.5x,J(0.5) ≈ 0.58
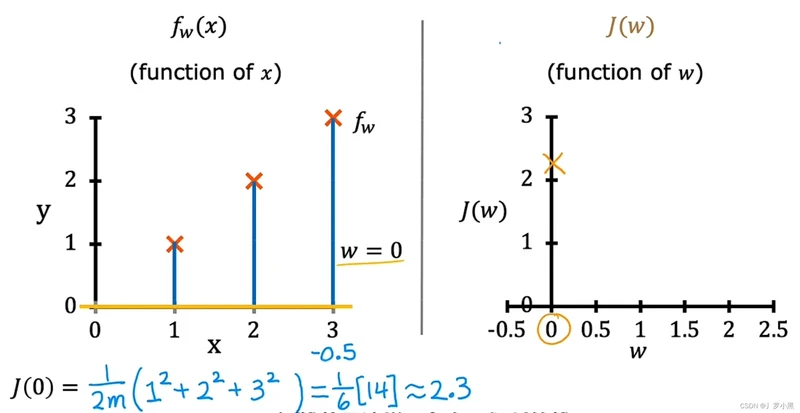
- 当w = 0时,f(x) = 0,J(0) ≈ 2.3
- 以此类推,多取几个点,再画出J(w)函数图像
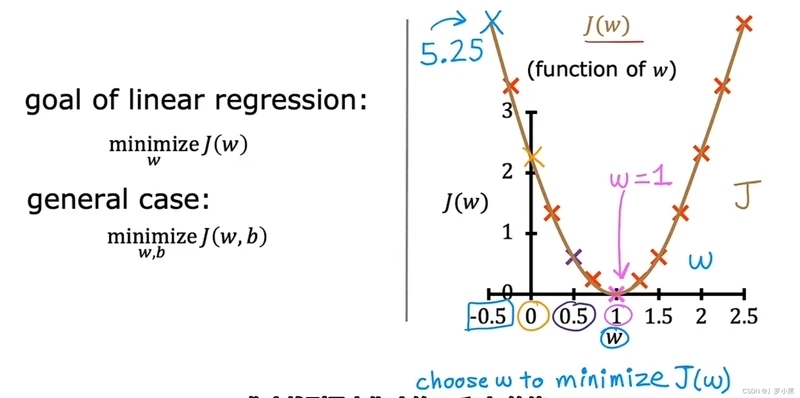
- 简化后的平方误差成本函数的目的是:找到一个w,使J(w)的值最小
- 一般的平方误差成本函数的目的是:找到一组w和b,使J(w,b)的值最小
3. 一般的平方误差成本函数
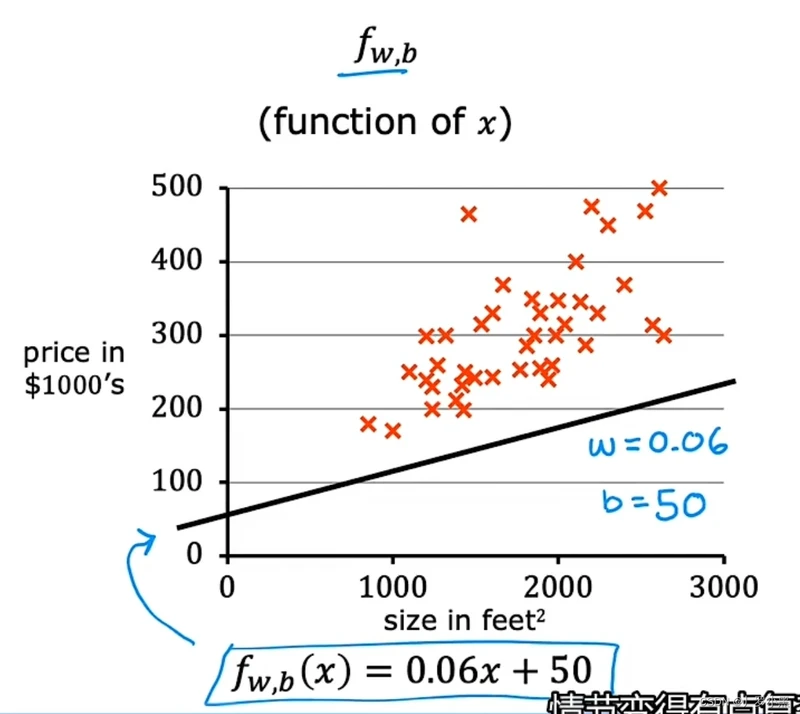
- 一个房子大小和价格的训练集,以及 w = 0.06,b = 50时的模型函数f(x)
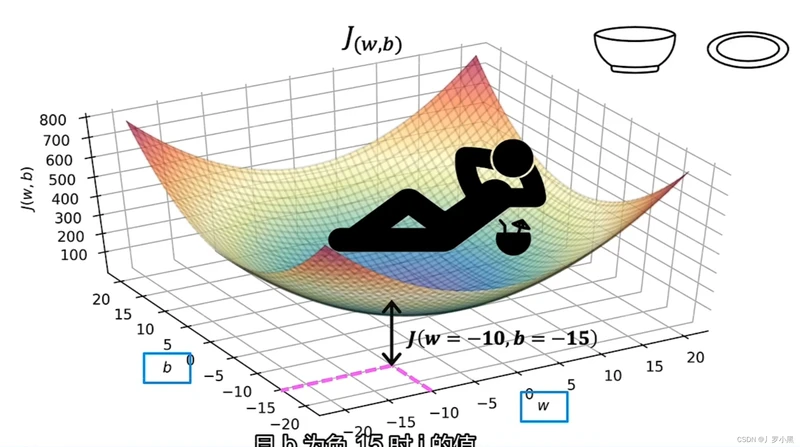
- 对应成本函数的3D曲面图,x轴为b,y轴为w,z轴为J(w,b)
- J(w = -10,b = -15) 是 w为-10,b为-15时,J函数的值
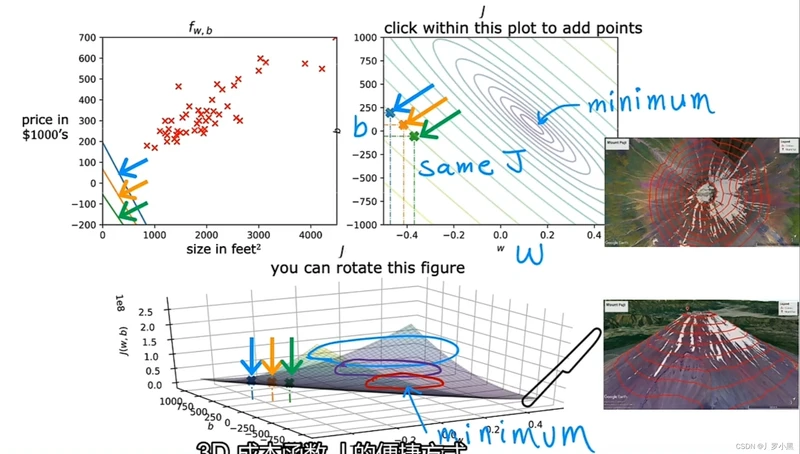
- 右上角的为成本函数的等高线图,同一条线上的J值均相同。等高线图中的椭圆中心点是J函数的最小值
- 等高线图上蓝,绿,黄三点表示左上角图中的三条线所对应的J函数的值,也表示下方图中的三点所对应的J函数的值
- 等高线图是可视化3D成本函数J的便捷方式,但它是2D形式的
- 拥有平方误差成本函数的线性回归,他的J函数总是弓形或吊床形的
